Кинетическая энергия твердого тела

Кинетическая энергия твердого тела

При применении теоремы об изменении кинетической энергии системы часто приходится вычислять кинетическую энерпно движущегося твердого гела. Найдем ее выражение при важнейших видах движения тела.

Тело движется поступательно

Пели тело движется поступательно, то скорости всех его точек в каждый момент равны между собой. Следовательно. в данном случае кинетическая энергия тела

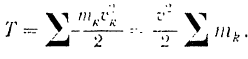
Обозначая 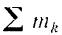через 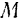получаем

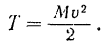
Кинетическая энергия 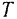поступательно движущегося тела равна половине произведения массы 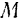тела ни квадрат его скорости .

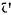Таким образом, кинетическая энергии поступательно движущегося тела, как этого и можно было ожидать, вычисляется совершенно одинаково с кинетической энергией материальной точки.

Но формуле (208) вычисляется также и кинетическая энергия любой системы, движущейся так, что модули скоростей всех ее точек одинаковы.

Тело вращается вокруг неподвижной оси.

Модуль 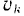скорости любой 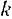-й точки тела, вращающегося вокруг неподвижной оси. равен произведению угловой скорости 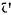тела на расстояние 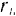, длиной точки от оси вращения тела. Следовательно, в данном случае кинетическая энергия тела

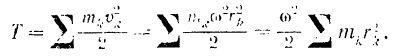
Но

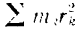
есть момент инерции 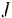тела относительно его оси вращения.

Следовательно, при вращательном движении тела

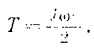
Кинетическая энергии 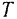тела, вращающегося вокруг неподвижной оси. равна половине произведения момента инерции 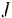тела относительно оси вращения не квадрат его угловой скорости .

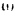Сравнивая формулу (209) с формулой (208) можно заметить что строение их аналогично. В формуле (209) роль линейной скорости точки играет угловая скорость тела, а роль массы момент инерции тела (мера его инерции при вращательном движении.

Тело совершает плоское движение.

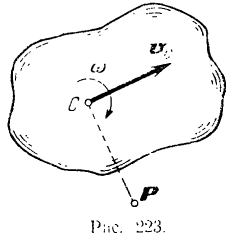
Пусть тело совершает плоское движение. Представим себе сечение тела (рис. 223) плоскостью проходящей через центр тяжести 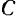тела н параллельной данной неподвижной плоскости. Допустим, что известна угловая скорость 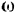тела и скорость 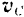центра тяжести тела.

Зная это. нетрудно найти и положение мгновенного центра скоростей фигуры. Он лежит (см. § 63) па перпендикуляре. восстановленном из какой-либо точки фигуры к направлению скорости этой точки, на расстоянии, разном отношению скорости данной точки к угловой скорости фигуры. Следовательно, искомое расстояние

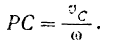
При плоском движении тола скорости его точек каждый момент распределяются так, как будто бы тело вращается в этот момент вокруг мгновенной оси (см. § 64), проходящей через соответствующий данному моменту мгновенный центр скоростей фигуры и перпендикулярной к ее плоскости.

Но кинетическая энергия тела

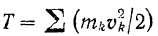
зависит только от массы каждой его точки и ее скорости, и поэтому соответствующую данному моменту кинетическую энергию тела, совершающего плоское движение, можно вычислить по формуле (209):

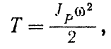
где 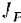— момент инерции тела относительно его мгновенной оси вращения.

Пользование формулой (209) для нахождения кинетической энергии тела при его плоском движении затрудняется тем, что требует для каждого момента времени определения положения мгновенной оси вращения тела и вычисления соответствующего ей момента инерции тела. Преобразуем полученную формулу, воспользовавшись теоремой о моментах инерции относительно параллельных осей (§ 80). Согласно этой теореме

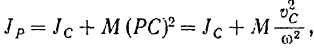
где 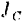— момент инерции тела относительно оси, проходящей через центр масс тела и параллельной мгновенной оси, 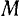— масса тела, 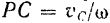— расстояние между рассматриваемыми параллельными осями.

Подставив полученное выражение для момента инерции 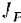тела относительно мгновенной оси в формулу кинетической энергии, найдем:

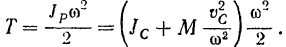
Раскрыв скобки и произведя сокращение, окончательно получим:

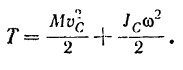
Кинетическая энергия тела при его плоском движении равна сумме тех кинетических анергий, которые имело бы данное тело при его поступательном движении со скоростью центра масс тела и при его вращательном движении вокруг оси, проходящей через центр масс тела и перпендикулярной к неподвижной плоскости, параллельно которой движется тело.

Данную формулировку нетрудно запомнить, если принять во внимание, что всякое плоское движение может быть разложено на поступательное движение со скоростью полюса и вращательное движение вокруг полюса (§61).

Только в отличие от кинематики выбор полюса здесь не произволен. При вычислении по формуле (210) кинетической энергии тела при его плоском движении за полюс надо обязательно выбирать центр масс тела. Если за полюс принять другую точку тела, то мы получим иную, чем (210), формулу для его кинетической энергии.

Пример задачи:

Маховое колесо (рис. 224), пес обода которого 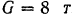, имеет наружный диаметр 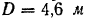и толщину обода 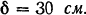. Какой момент силы нужно приложить к маховику, чтобы после 200 оборотов его угловая скорость была равна 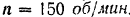. Момент инерции спиц и втулки маховика принять равным 10% момента инерции его обода. Весом вала и трением в подшипниках пренебречь.

Решение:

По теореме о кинетической энергии системы

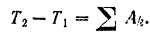
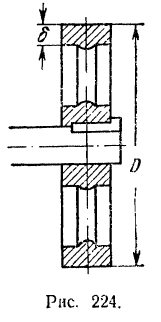
Кинетическую энергию маховика в конце рассматриваемого периода его работы определим по формуле (209) 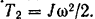Так как в начальный момент маховик был неподвижен, то его кинетическая энергия в этот момент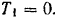

Изменение кинетической энергии маховика происходит только за счет приложенного к нему постоянного вращающего момента, работа которого согласно формуле (202) равна

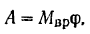
где 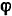— угол поворота в радианах.

Таким образом, уравнение кинетической энергии системы принимает вид

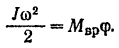
Отсюда искомый момент сил равен

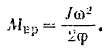
Момент инерции 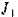обода маховика найдется ил формулы (145) для полого круглою цилиндра

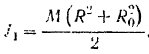
Наружный радиус обода

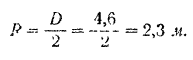
Внутренний радиус обода

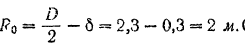
Следовательно, момент инерции обода

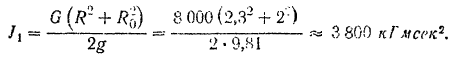
Момент инерции спиц и втулки

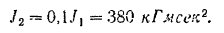
Момент инерции всего маховика

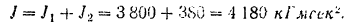
Угловая скорость маховика

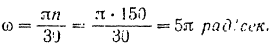
Угол, на который повернется маховик, сделав

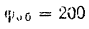
оборотов, равен

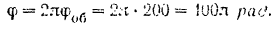
Подставляя числовые данные, определяем весомый момент сил

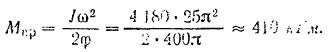
Пример задачи:

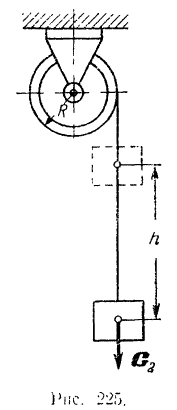
На шкив (рис. 225) радиуса 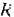весом 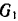навернута веревка, к концу которой подвешен груз весом 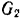. Сначала система находится в покое. Найти угловую скорость шкива в тот момент, когда груз опустится на высоту 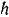. Массу шкива считать равномерно распределенной по его наружной поверхности. Трением пренебречь.

Решение:

Так как система сначала находилась в покое, то се начальная кинетическая энергия 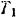равна нулю. Кинетическая энергия 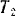системы будет складываться из кинетической энергии 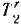самого груза в кинетической энергии 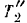приводимого им во вращение шкива. Так как скорость 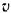груза связана с угловой скорости 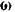шкива зависимостью 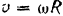то кинетическая энергия груза равна

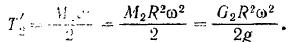
Кинетическая энергия шкива равна

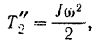
где 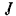— момент инерции шкива, который вычисляем по формуле:

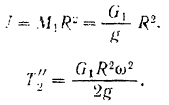
А кинетическая энергия всей системы

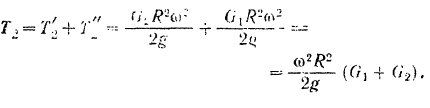
Так как кинетической энергии системы происходит только за счет работы силы тяжести опускающегося на высоту 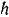груза, то и уравнении (207) кинетической энергии системы надо положить

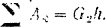
Таким образом, уравнение кинетической энергии системы приобретает вид

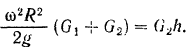
Отсюда искомая угловая скорость шкива

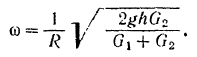
Пример задачи:

Танк (рис. 226) приводится в движение двигателем. который вращает четыре колеса (по два с каждой стороны). Колеса своими выступами захватывают гусеницы. Определить скорость танка через 10 сек после начала его движения, если средняя полезная мощность двигателя танка 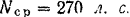. все танка без колес и гусениц 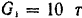, вес каждой гусеницы 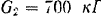. вес каждого колеса 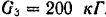. Колеса считать однородными сплошными цилиндрами.

Решение:

Рассматриваемая система состоит; 1) из поступательно движущегося корпуса танка, 2) двух гусениц, каждая из которых движется поступательно вместе с танком и одновременно с той же скоростью совершает движение относительно корпуса танка, и 3) четырех колес, вращающихся вокруг своих осей и вместе с ними перемещающихся поступательно, т. е. совершающих плоское движение.

Кинетическая энергия корпуса танка равна

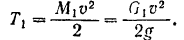
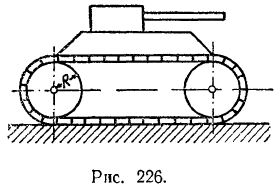
Кинетическая энергия гусениц

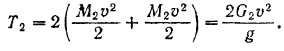
Скорость точек оси колеса равна поступательной скорости танка. Следовательно, угловая скорость колеса 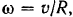где 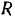—радиус колеса. Момент инерции колеса (сплошного цилиндра)

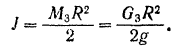
Таким образом, кинетическая энергия колес:

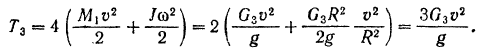
Кинетическая энергия всего танка

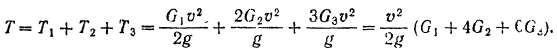
Так как в начале движения танка его кинетическая энергия равна нулю, то уравнение (207) кинетической энергии системы принимает вид

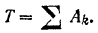
Следовательно, полезная работа двигателя, приводящего в движение танк,

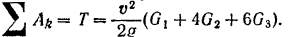
Средняя полезная мощность двигателя (в лошадиных силах)

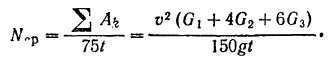
Отсюда скорость танка через 10 сек после начала его движения

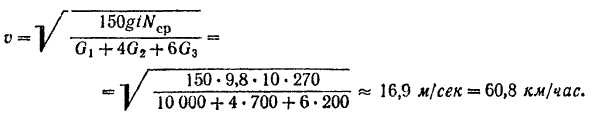
Пример задачи:

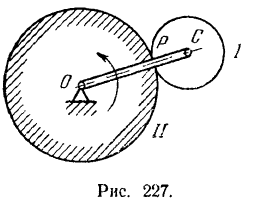
Шестерня I (рис. 227), ось которой проходит через точку 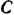С кривошипа, при вращении кривошипа 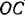вокруг неподвижной оси катится по неподвижной шестерне II. Механизм (планетарный) расположен в горизонтальной плоскости и приводится во вращение из состояния покоя посредством вращающего момента 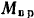, приложенного к кривошипу.

Радиус шестерни I (сателлита) — 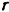, ее вес 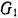. Радиус неподвижной шестерни II — 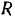. Вес кривошипа равен 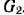. Пренебрегая трением в осях, определить угловую скорость 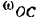и угловое ускорение 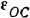кривошипа, в зависимости от его угла 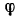поворота. Шестерню I принять за однородный диск, а кривошип — за однородный стержень.

Решение:

Рассматривая кривошип и шестерню I как одну систему, применим к ней теорему об изменении кинетической энергии системы:

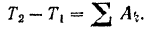
Так как вначале система была неподвижна, то .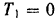

Находим кинетическую энергию 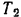системы в момент, соответствующий повороту кривошипа на некоторый произвольный угол .

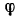Кривошип совершает вращательное движение вокруг неподвижной оси и его кинетическая энергия равна

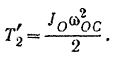
Момент инерции однородного стержня относительно оси, проходящей через его конец (задача 71).

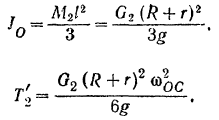
Шестерня I совершает плоское движение. По формуле (210) ее кинетическая энергия

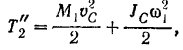
где 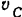— абсолютная скорость центра 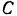масс шестерни I и 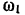— ее абсолютная угловая скорость.

Точка 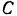является общей точкой шестерни I и кривошипа 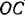. Следовательно:

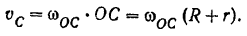
Мгновенный центр 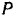скоростей шестерни I, катящейся без скольжения по неподвижной шестерне II лежит в их точке касания. Скорость точки 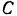шестерни I нам известна. Отсюда абсолютная угловая скорость шестерни I:

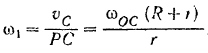
Момент инерции шестерни I (однородного сплошною цилиндр) относительно ее центральной оси:

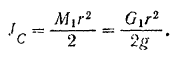
Подставляя найденные значения угловой скорости, скорости центра масс и момента инерции в выражение для кинетической энергии шестерни I, находим:

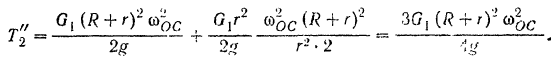
Кинетическая энергия осой системы

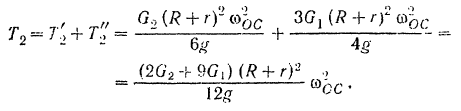
Вычисляем теперь сумму 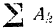, работ всех сил, приложенных к системе, при повороте кривошипа на угол .

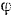Механизм расположен в горизонтальной плоскости. Следовательно, работа сил тяжести, приложенных ко всем частям системы, равна нулю. Трением в осях мы пренебрегаем. Таким образом, изменение кинетической энергии нашей системы происходит только за счет работы постоянного вращающего момента 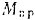, приложенного к кривошипу.

Таким образом, в соответствии с формулой (202)

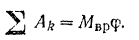
Подставляя найденные значения

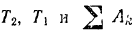
уравнение кинетической энергии системы, получаем:

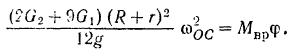
Отсюда искомая угловая скорость кривошипа

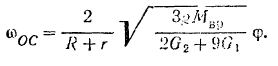
Для того чтобы определить угловое ускорение кривошипа, продифференцируем по времени обе часта уравнения кинетической энергии:

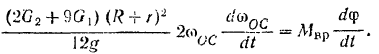
Принимая во внимание, что

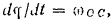
и сокрушая на 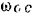, обе части последнею равенства, находим:

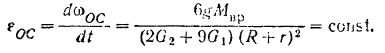
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:

Теоретическая механика — задачи с решением и примерами

Возможно вам будут полезны эти дополнительные темы:

Работа и мощность силы, приложенной к вращающемуся телу с примером решения

Теорема об изменении кинетической энергии точки с примерами решения

Метод кинетостатики в теоретической механике с примерами решения

Определение динамических реакций опор вращающегося тела