Оглавление:




Кинетическая энергия в относительном движении
- Используя уравнение 4, можно четко выполнить все аналитические преобразования, сделанные при исследовании абсолютного движения. Например, если умножить уравнения 4 на dx, dy и DZ соответственно, а затем сложить их вместе, то можно получить результат, аналогичный тому, который приводит к кинетической энергии theorem. В результате терм, производный от силы инерции Кориолиса, исчезает, как следует из уравнения 5, и уравнение ДМВ 2 = Xdx + г ды Здз м п х DX Г Е Г ды м п з ДЗ. В результате разность кинетической энергии точки в относительном движении равна фундаментальной работе силы, приложенной к точке, и несущей силы инерции на практике.
Тот факт, что работа сил инерции Кориолиса равна нулю, следует из того, что эта сила перпендикулярна относительной скорости Vr, а также перпендикулярна относительному перемещению dx, dy, dz. Родственник equilibrium. To получаем уравнение относительного равновесия, нам нужно Поло d2x d2y D2Z dx DY dz в предыдущем уравнении. Аналогично живут равны нулю. Как Естественно, j также становится нулем, и он становится: A =0.Г м п г = 0, З М Е С = 0 Поэтому для составления уравнений относительного равновесия необходимо описать, что сила F уравновешивается центробежной силой. Точки, в которых координаты x, y, z соответствуют этим 3 формулам, определяют положение относительного равновесия.
Ту же теорему можно выразить в следующей форме: Кинетический момент системы, относительно точки О равен кинетическому моменту относительно точки О всей массы в предположении, что она сосредоточена в центре тяжести, сложенному с кинетическим моментом системы в ее относительном движении вокруг центра тяжести, взятым относительно этого центра тяжести. Людмила Фирмаль
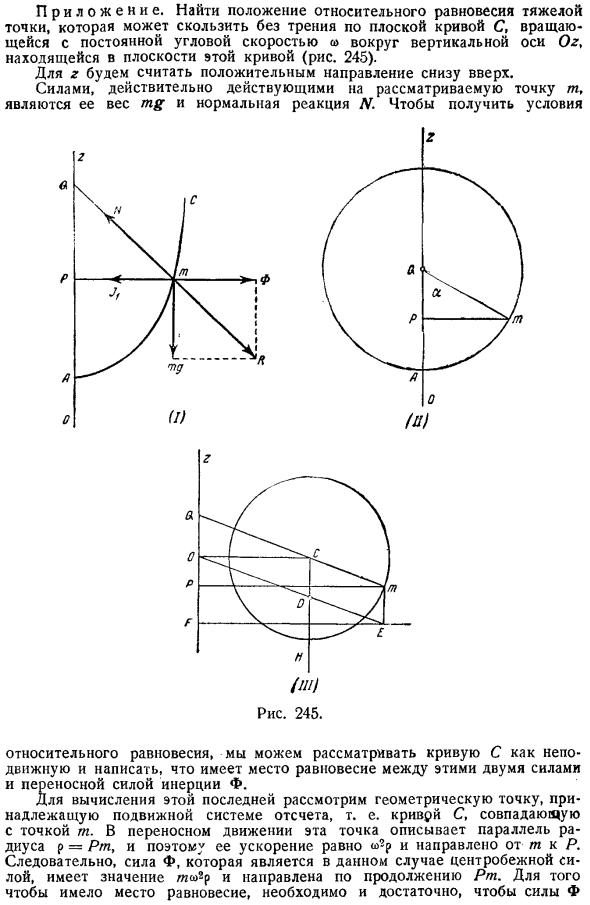
Если вы приводите движущуюся точку в это положение, не сообщая начальную относительную скорость, то относительная скорость равна нулю из 3 сил, которые вызывают относительное движение точки, а другие 2 уравновешиваются, так что 1, или сила инерции Кориолиса, равна extinguished. As в результате пункты остаются относительно мирными. Приложение. Найти положение относительного равновесия упора, который может скользить без трения в плоскости кривой C, которая вращается с постоянной угловой скоростью o вокруг вертикальной оси Oz в плоскости этой кривой рис.245. для z мы предполагаем, что направление снизу вверх является положительным.
Рассматриваемый момент это сила, которая реально действует на м его массу mg и нормальная реакция N. В относительном равновесии мы можем видеть, что кривая C не движется, и мы можем написать, что существует баланс между этими 2 силами и пропорциональной и инерционной силой F. Для вычисления последней рассмотрим геометрические точки, принадлежащие движущейся системе отсчета, то есть кривую с, совпадающую с точкой m. In подвижное движение, эта точка представляет собой параллельную линию радиуса p = Pm, и поэтому ее ускорение равно, направленное от m к P. Таким образом, сила Ф, которая в данном случае является центробежной силой, имеет значение mufy и направлена вдоль продолжения PT.
Для того чтобы наступило равновесие, необходимо и достаточно, чтобы силы и mg были в результате перпендикулярны кривой. Из этих треугольников mPQ и pF У нас есть Итак, положение равновесия это точка кривой, где ненормальное PQ равно, а точка Q пересечения нормали и оси z должна находиться выше точки P. At точка а, когда p = 0, касательная равна горизонтальной скорости вращения. Например, предположим, что данная кривая представляет собой параболу с вертикальной осью, вращающейся вокруг этой оси. За исключением того, что параболические параметры равны, вершина становится единственным положением равновесия, и в последнем случае все точки параболы удовлетворяют условиям в question.
- В результате свободная поверхность жидкости, которая совершает равномерное вращательное движение вдоль вертикальной оси, является параболоидом вращения. Это происходит потому, что каждая частица жидкости на поверхности может быть уподоблена тяжелой материальной точке, которая может скользить по меридиану без трения. Если заданная кривая представляет собой окружность с радиусом R рис. 245, и ее центр Q находится на оси вращения, то условие равновесия принимает вид: п Qп = Р соз а=, потому что = Поэтому, чтобы баланс существовал В отличие от A, w это В основе лежит теория Водяного регулятора паровых двигателей.
Если данная кривая представляет собой окружность с радиусом R, где центр C не находится на оси вращения, то существует 2 или 4 равновесия positions. To предложив аналитическое решение в качестве упражнения, мы ограничимся следующими замечаниями рис. 245,. M положение равновесия, QP соответствует ненормальному, O проекция центра C на ось вращения Oz. Проведем прямую линию OE, равную Qm и параллельную Qm, возьмем OD = QC, DE Cm R. ось EE через E, которая перпендикулярна Oz, занимает известное положение, так как OE = QP=. Ось CDH также занимает известное положение, поскольку она параллельна оси Oz axis. In кроме того, DE =R. прямая линия DE, равная R, проходит через указанную точку O.
Шесть первых уравнений содержат только внешние силы. Теоремы кинематики для вычисления моментов количеств движения и кинетической энергии 347. Людмила Фирмаль
Ее ребра E и D опираются на указанные 2 вертикальные оси CH и EE, и нахождение положения равновесия сводится к геометрической задаче. Рисует прямую линию через точку O. 2 фиксированные сегменты оси длины R, к которым отрезаны CH и EE. Радиус St параллелен этому line. It известно, что эта геометрическая задача имеет 2 или 4 решения, в зависимости от того, находится ли точка O снаружи или внутри epithyloid. An эпителий представляет собой оболочку отрезка длиной R, концы которого скользят по 2 осям CH и EE. Этот результат был получен Гильбертом из уравнения равновесия. Гилберт, Лагранжа АУ движение относительный, Анналес де ла Сосьете научно Тихуана де Брюссель, 1883.Отмечать.
Если необходимо найти движение точек вдоль кривой C рис.245, Z , то достаточно применить теорему о кинетической энергии к относительному движению. Основная работа веса равна mg dz, а основная работа центробежной силы равна m o2p dp, а работа кориолисовой инерционной силы равна нулю. Энергетический Интеграл получается в следующем виде mv2r = мгз + mw2p2 сек. Чтобы получить положение относительного равновесия, функция силы справа должна найти положение максимальной или минимальной движущейся точки. Максимальное значение этой функции соответствует положению конюшни equilibrium.
Для круга, который вращается вокруг оси, проходящей через его центр, если только такое положение существует, мы можем видеть, что положение равновесия точки А стабильно рис.245, ZZ .Но если точка может занимать другое положение равновесия m, то это же положение будет неустойчивым.
Смотрите также:
Теоретическая механика — задачи с решением и примерами
Если вам потребуется заказать теоретическую механику вы всегда можете написать мне в whatsapp.

