Оглавление:


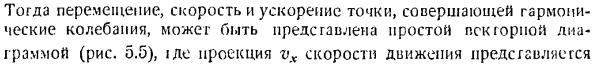



















Кинематика колебаний
- Кинематика качания 1°.Гармоническая вибрация. Вибрацией или вибрационным процессом называют такую степень изменения, причем непрерывно увеличивающуюся и уменьшающуюся. Самым простым и в то же время самым важным видом вибрации является гармоническое колебательное движение. Рассмотрим круг с радиусом a(рис. 5.4).Нарисуйте 2 перпендикулярных друг другу диаметра, которые проходят через центр окружности в точке O.
направление горизонтального диаметра считается осью x, а ось y ориентирована в сторону вертикального диаметра. .До ю = ЦУВ Решение. выберите абсолютную систему координат xy, содержащую начало координат и точку движения O, так чтобы ось x совпадала с относительной осью l. после этого абсолютное движение точки определяется координатами йк = ом = jc0-5-МПМ потому что(АТФ) ’ \ — а. Я ведь(КТ (!!))
Вращайте круг радиуса равномерно вокруг центрального круга с умной скоростью K. Людмила Фирмаль
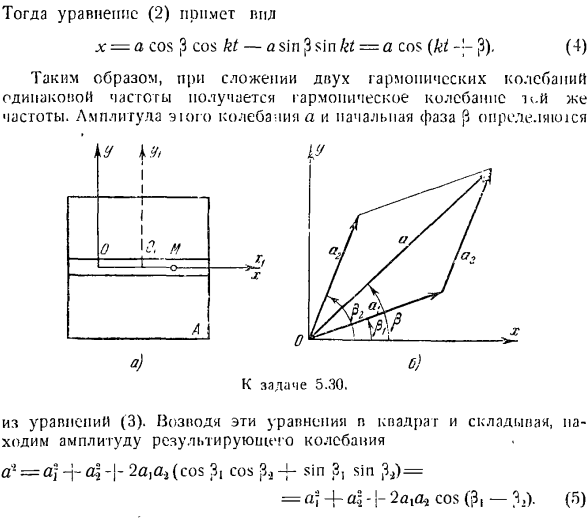
Итак, задача будет состоять в суммировании 2 гармонических колебаний одинаковой частоты, а следовательно, одного и того же периода, с разной амплитудой и начальной фазой. Если вы откроете Косинус суммы 2 углов на правой стороне (I), это выглядит так: = потому что 3, потому что 3.) потому что КТ-(а, грех-п — ф — ^ грех грех КТ.(2) Введем новую константу а и свяжем ее с исходной величиной по следующему уравнению: а потому что п-я, потому что я а \ грех я = 3j грех О2 грех Цзи 次に 、 式 (2) 、 、 式 (I )далее, формула (2) х = а соѕ 3 потому что КТ-грех, грех 3 КТ = а соѕ (КТ(4)
Итак, если суммировать 2 гармонических колебания одинаковой частоты, то получаются гармонические колебания одинаковой частоты. Амплитуда колебаний Юго а и начальная фаза адгезива Р АУ У МЕНЯ Ю> З Я! Цель 5.30. Из Формулы(3).Найти амплитуду результирующего колебания, возведя эти уравнения в квадрат и сложив их а Прис = ajh начиная-ФЗ | — / — 2а, АИ(cos3i J В ^ — й-3 грех, грех = Дя + аз-1 — 2axd2 Кос -?(.). (5) Найти начальную фазу колебаний, разделив 2-е из Формулы(3) на 1-е. Б 1 уй «.ОС П 4 » А2 c0s и1 * Из формул (5) и (P>) следует
- Следующий простой геометрический метод определения результирующей вибрации: отложите вектор a длины a, наклоненный от начала координат 0 (рисунок B) относительно оси x, и вектор a*, наклоненный^относительно оси X. Найти сумму этих 2 векторов как диагонали параллелограмма, построенного на этих векторах. Длина диагонали соответствует амплитуде результирующего колебания, а угол наклона относительно оси x определяет начальную фазу этого колебания.
Этот прием геометрического сложения 2 гармонических колебаний одинаковой частоты, направленных вдоль 1 Прямой линии, легко распространяется на сложение любого числа таких oscillations. It достаточно отложить от нескольких произвольных полюсных векторов, пропорциональных амплитуде составляющих колебаний с наклоном, равным начальной фазе. Если сумма этих грудных клеток повреждена пулями, то точки не сдвинутся.
Сумма этих векторов определяет амплитуду результирующей вибрации, а угол ее наклона определяет начальную Фаза Людмила Фирмаль
Задача 6.31.Точка M следует уравнению для выполнения линейного гармонического колебательного движения вблизи RA 0. ху = −0 \ соѕ(мл-с). В этом случае основание механизма вместе с точкой 0\ также совершает линейное поступательное гармоническое колебательное движение. Вблизи неподвижного центра O по экватору * 0%С () С(П — £О)- В Nairan-1 Leppu оба колебания совпадают, и интервал между частотами этих колебаний m-n очень мал по сравнению с самой частотой. Определите уравнение абсолютного движения Йорк м х = х,+ x0i = Д], потому что(т -£.) — • — а потому что(НТ — £0). (1) платить g> 31. PGSS создает результат
следующим образом: TOGETEST-заменить Peppo Его «s (nt — £0) — cos [mt — ( / / ; — n) i-е»|, (2) к) да л ’ = р, потому что(т-р) а {) потому что | т-(п-п) т-З0]- — {Г/, потому что-р-р, потому что р [(//- п) т s0j} потому что т-р — Дж — {ДТ ц0 грех грех от ZJ [(м-н) т — {- Е0 \ грех инт. (3) Создайте новые переменные r и 0, удовлетворяющие уравнению. rcos 0 = АИ, потому что е — О0 потому что[(///-//)/е0), к| ф грех 0 = а j греха-Джей-грех (/////) Т Е0 |.Дж (4) Уравнение абсолютного движения точки(3) можно выразить следующим образом: х — = р соз(Т-0), (о) Где R и 0 определяются из»(4).Возьмем уравнение в степени 2 и возьмем в степени 2: р = г] — Ф \ — Джей-Кос-Н) (- П-Е0-е].(си)
Если разделить равенство (4) на другое, то можно увидеть следующее: т е 0 = » это ’ НК ’+ flosin Эм-п)т + т (, \ *О, ко,-Т-«Орос [////- п) т-р Е0 «Дж• Из уравнения (o) результирующее колебание можно рассматривать приблизительно harmonic. In в этом случае амплитуда r и начальная фаза 0 не являются постоянными величинами, а медленно изменяются во времени functions.
By предположения, частота изменения этих величин m-n очень мала по сравнению с частотой колебаний компонентов. Из уравнения (b) видно, что амплитуда абсолютных колебаний изменяется в пределах rm3X = al r1 / Nl = a, — o0. Часто этот вид движения, наблюдаемый в различных областях техники, называют assault. In цифра, буква Ti обозначает период пульсации, а буква-период нарастания вибрации. Овладеть навыком решения задачи о гармонических колебаниях, I. V. It рекомендуется решить следующие задачи из»сборника задач и теоретической механики»
по изданиям Мещерского после 1950.310 、315、325、326、329、350。 2e. негармоничная школа и I Если 2 или более гармонических колебаний разной частоты происходят вдоль 1 Прямой, если частоты составляющих движения равны, то периодическое негармоничное движение является obtained. In кроме того, непериодические колебания часто встречаются в природе и технике. Напомним, что регулярные движения называются быстрыми движениями, и через некоторое время они повторяются полностью. В данном разделе рассматривается кинематика этих движений.
Для решения проблем, описанных в этом разделе, рекомендуется выполнить следующие действия. U: 1) Выберите оси. 2) Создайте уравнение вибрационного движения. 3) суммирование колебательного движения, которое является результатом уравнения результирующего движения. 4) Определите скорость и ускорение точек. Задача 5.32.Точки перемещаются в соответствии с уравнением х = топор грех (комплект ч-п.)- г грех(к, Д-Г;!.), (1)
Кроме того, период составляющих гармонических колебаний уравновешивается. То есть соотношение рациональное. Где rii и Po-целые числа, а дробная часть(2) неприводима. Определите длительность возникающих колебаний. Решение. Движение точек суммируется в соответствии с (I) из 2 гармоник. Из равенства(2) нл \ = n1T1. (:\) Если обозначить эти равные произведения буквой G, то получим период колебания результата, поскольку за время T (1) оба члена возвращаются к своим исходным значениям, а минимальное целое число периода обеих гармоник повторяется за этот период.
Заметим, что если период составляющей вибрации не является сократительным, то существует период результирующего движения, причем движение в этом случае непериодическое. Задача 5. 33.Точки перемещаются в соответствии с уравнением. х = ае п < грех (^/Р *-nlt3). Определите период колебаний, законы уменьшения амплитуды колебаний с течением времени, скорость и ускорение точек. Решение. Прежде всего, следует отметить, что это движение является колебательным и непериодическим. *(Т;-Т)= Х(О-
Под периодом полных колебаний мы понимаем период, в течение которого переменная x изменяется от максимального значения к другому. Чтобы найти период, сначала найдите время, в которое переменная x принимает значение extremum. To сделайте это, сделайте производную от l * равной, но время равно нулю Х = ае НТ [- Н грех (данные-1-?) + Cos (kjt-f- $)] = 0、 Здесь для краткости Ar2 = | / 1r-gg. Я найду тебя отсюда.: тг(* ихъ?) = р|(-) Учитывая непрерывное значение времени, удовлетворяющее уравнению (1) в ti, и то, что периодичность касательной соответствует изменению аргумента из-за значения tg, получается следующее уравнение: * я ’<+ я- + +?) = *•(2) * И4 с TI.
t соответствует последующим максимальным и минимальным значениям, поэтому разница между ними равна половине периода. Затем найдите следующее из(2): __т т.-* Или Вернемся к определению закона уменьшения амплитуды колебаний с вращением во времени. Найти значение из (1) грех (*, м — * { -£)= 1 ′ 1 г-ф п-• В этом случае соседним экстремумом является переменная (амплитуда колебаний), которая выглядит так: грех(дунь-и J = ае-нТл ^ ЛР-РТ Мг-г л -’ a,= j (fH f)| mf «’ in — отношение 2 последовательных амплитуд ПГ| НТ !Логарифм обратной величины 2 называется логарифмическим декрементом, который характеризует скорость уменьшения амплитуды.
Найти скорость точки ЧХ = х = ае НФ \ ки соѕ {kxt-л грех Ускорение точки определяется как 2-я производная от временной координаты серии WX = х = н / 1-2 / / а -, потому что (kxt п) (л* -/•}) грех(/, г-Ж-Г) Дж. Начальное время радиуса OL0n, t =О, определяется углом 3.Тогда угол поворота радиуса ОА определяется по формуле: И что? = «+П. Да.*) Напишите уравнение, опустив точку A перпендикулярно оси x Перемещение точки B а = о грехе(КТ 3). (2 *) Это гармоники гармоники. Где а-амплитуда, то есть максимальное расстояние от средней точки. Расстояние между крайними положениями точек называется диапазоном качания.
Под периодом полных колебаний мы понимаем период, в течение которого переменная x изменяется от максимального значения к другому. Чтобы найти период, сначала найдите время, в которое переменная x принимает значение extremum. To сделайте это, сделайте производную от l * равной, но время равно нулю Х = ае НТ [- Н грех (данные-1-?) + Cos (kjt-f- $)] = 0、 Здесь для краткости Ar2 = | / 1r-gg. Я найду тебя отсюда.: тг(* ихъ?) = р|(-)
Учитывая непрерывное значение времени, удовлетворяющее уравнению (1) в ti, и то, что периодичность касательной соответствует изменению аргумента из-за значения tg, получается следующее уравнение: * я ’<+ я- + +?) = *•(2) * И4 с TI. t соответствует последующим максимальным и минимальным значениям, поэтому разница между ними равна половине периода.
Затем найдите следующее из(2): __т т.-* Или Вернемся к определению закона уменьшения амплитуды колебаний с вращением во времени. Найти значение из (1) грех (*, м — * { -£)= 1 ′ 1 г-ф п-• В этом случае соседним экстремумом является переменная (амплитуда колебаний), которая выглядит так: грех(дунь-и J = ае-нТл ^ ЛР-РТ Мг-г л -’ a,= j (fH f)| mf «’ in — отношение 2 последовательных амплитуд ПГ| НТ !Логарифм обратной величины 2 называется логарифмическим декрементом, который характеризует скорость уменьшения амплитуды.
Найти скорость точки ЧХ = х = ае НФ \ ки соѕ {kxt-л грех Ускорение точки определяется как 2-я производная от временной координаты серии WX = х = н / 1-2 / / а -, потому что (kxt п) (л* -/•}) грех(/, г-Ж-Г) Дж. Начальное время радиуса OL0n, t =О, определяется углом 3.Тогда угол поворота радиуса ОА определяется по формуле: И что? = «+П. Да.*) Напишите уравнение, опустив точку A перпендикулярно оси x Перемещение точки B а = о грехе(КТ 3). (2 *) Это гармоники гармоники. Где а-амплитуда, то есть максимальное расстояние от средней точки. Расстояние между крайними положениями точек называется диапазоном качания.
После того, как простое преобразование найдено C’D = — k’L lx-2 px、 | de указывается, как и прежде. / Р К \ р н \ Итак, ускорение точки состоит из 2 частей: ускорения, которое пропорционально отклонению точки или r от центра вибрации, и ускорения (торможения), которое пропорционально скорости. Задание 5.34: точки перемещаются в соответствии с уравнением. х = грех я 2Ш /- \ (.т. к.\ y = грех! о) т—•» -:. 2 J
Определяет траекторию, скорость и ускорение точки. Решение. Опишите уравнение движения точек следующим образом: Х = — О, потому что 2 <О /,(1) y = — такой* вес. (2) Чтобы исключить время из системы уравнений, преобразуем уравнение(1)следующим образом: x—a (sin1-cos-u)/)= a (I-2 cos о*) подставим значения в это уравнение cos w / = — y’a、 Мы получаем: −2 г) Или Это уравнение параболы с вершинами в точке (a, 0), a! X-это ось симметрии. Траектория точки, как видно из формул(I)и(2), представляет собой отрезок этой параболы, окруженный квадратом со стороной 2e.
Найти проекцию скорости точки, дифференцируя уравнения движения (1) и (2). ЧХ-х = 2 <Ри> грехов 2(<(4) вы = Р = грех <•> *в. (0) Найти скорость точки отсюда в =грех (от(4 потерь J). Проекция точечного ускорения выглядит так: серии WX = х = 4flcu-Кос =-4У)!Х, ПМР = г =■= f = 1, cosw^ = — I; Точка//: cos2®> / = 1, cos wt — — — I; Для точки C: cos 2m =-1, cos » > / = 0. один. Тогда из формул(4)и(5) следует, что скорости точек A и B равны скорости пули, а в точке C ВК-X = м, vCy=±: Аой、 Кроме того, знак зависит от направления, в котором движется точка (от А до В или наоборот).
Точка ускорения указанного положения sin определяется путем подстановки координат (6). = — 4и-Дж-г), ЗП =уя(4-я-Р-К), сан. узел =-4 так-ай. Для овладения навыком решения задачи о негармоничных колебаниях Сборник задач теоретической механики И. В. Мещерского рекомендует решать следующие задачи в изданиях начиная с 1950 года: 314, 328 и 357. Угол z>, определенный в Формуле (1*), называется осциллирующей фазой, а угол p-начальной фазой. Цикл колебаний-время, за которое точка совершит 1 полное колебание, равно следующему 2г. Т. Обратный (4 *)
Она называется частотой вибрации и измеряется в частоте в единицу времени. Если это занимает 1 секунду в единицу времени, частота вибрации измеряется в Герцах(G. In отбросы гарна). величина k называется частотой циркуляции или частотой обращения. Как видно из (4), значение k равно частоте 2m: единице времени (например, 2 секунды). Если рассматривать ОА как вектор, вращающийся с угловой скоростью k, то гармоническое колебание представляется его горизонтальной проекцией.
Скорость точки при гармонических колебаниях выглядит так: vx = x = ak cos(kt-j-3)(5) и его ускорение серии WX = х = — п / р * грех(/ Р/+£). G*) рисунок 5.5. \ У (\° А — «() » / Ф / ч. 1 / / л л Рисунок 5.4. (3 *) Т. Два〜 С и \ Г(1′ ► 1 0 \ / 1 x k \ y на следующем этапе движение, скорость и ускорение точки, совершающей гармонические колебания, можно представить в виде простой векторной диаграммы (рис.5.5).1DE представляет собой проекцию vx скорости движения Вектор OB горизонтальной проекции длины ak повернут на 90°относительно вектора OA длины a в том же направлении, что и направление вращения.
Проекция ускорения точки wx представлена горизонтальной проекцией вектора ОС длины a k1, повернутой на 180°относительно вектора OA. Все 3 вектора вращаются с угловой скоростью k вокруг центра O. таким образом, производная уравнения движения точки может быть интерпретирована как вращение вектора выражения в направлении поворота на 90°, с одновременным умножением p.
При решении задач, связанных с кинематикой гармонического колебательного движения, рекомендуются следующие действия: )) Выберите » sys 1 координата; 2)создать гармоническое колебательное уравнение движения «;; 3) суммируем гармоническое колебательное движение и получаем полученное уравнение движения. 4) определить скорость и ускорение точки гармонических колебаний.
Г)) определить траекторию движения точки при сложении гармонических колебаний, не направленных вдоль 1 линии. Задача 5.28.Точки совершают гармонические колебания вдоль горизонтальной оси Х. диапазон колебаний составляет 20 см, а длительность 10-5 секунд. Составьте уравнение движения точки, предполагая, что точка в первый момент/ = 0 находится в самом правом положении. определите точки фастиба и ускорения. Решение. Форма уравнения гармонических колебаний точек имеет вид
Исходя из условия задачи, константы a, A. ’, находим значение%.Амплитуда колебаний t равна половине амплитуды колебаний. Так… az = 10 см. Период колебаний определяется из длительности диапазона 10, то есть из условия, что 5 полных колебаний составляют около a second. So,
Длительность 1 полной вибрации или период колебаний может быть следующим: Т-1 секунда. Коэффициент k определяется по формуле периода колебаний(3*). Подставляя значение найденного коэффициента u (I), находим: x 10 sin(2tL-J-E). (2) Чтобы определить начальную фазу p, используйте начальную conditions. AT t-0, точка находилась в крайнем правом положении (если/ = 0, то ось x= 10 см. Когда вы вводите значение в (2), оно выглядит так: 10-10 Син С.、 где sin и p = m / 2.
Теперь уравнение гармонического колебательного движения Нравится А = 10 \ грех ’2-т-дж-дж Или, в конце концов、 х = 10 соѕ 2zt. В линейном движении проекция кратчайшей точки от оси равна первой производной oi координатного времени ЧХ = х =■ — 20nsin 2-т. Проекция ускорения точки на ось A * равна закону-производной от координаты времени серии WX = х—4С-Джей, потому что 2tL = — 4tt-а (3) IL(3) заключается в том, что ускорение точки при гармонических колебаниях всегда пропорционально отклонению и направлено к центру колебаний.
Задача 5.29.Точка D7 движется, но по формуле 5 = Ycm круг с радиусом ft = 10 см, 1De s — это пуп, пропущенный через луч. В первый раз точка M была в Л/»(рисунок A).Равномерное движение описываемой точки Af ho происходит в окружном направлении! Вы можете реализовать его с помощью механизма перед первой фотографией. a. механизм cocioni от слайдера L можно двинуть и направить вертикально. На ползунке имеется канавка I рынзалпала, в этом отношении м движется и участвует в сложном абсолютном движении одновременно с рысканием вдоль ползунка джнепина и табуретки.
Задача 5 / К со). Относительное движение и отношение движения к которому необходимо сообщить определяет уравнение движения: относительное движение к точке м вдоль первой горизонтальной канавки, а поступательное движение 2-й вертикальной направляющей к ползуну а выполняет заданное абсолютное движение точки. Решение. Определите угол MJOM = 3.Это радиус ом с осью Ox. ? — / Г-Р-К- Найти уравнение относительного движения точки, если мы знаем угол п x,= R cos E = 10 cos 0.5/, j>,= 0
Отношение базы механизма к уравнению движения в движении выглядит следующим образом. = 0, уа =sinsinэ = 10 Sin 0.5/. Таким образом, равномерное движение точки по окружности можно разбить на 2 взаимно перпендикулярных линейных гармонических колебания. Задание 5.30.Согласно закону, точка м движется по прямой в пустом параплане и фиксируется на борту А. ДГ〜а [потому, что(/ РТ-п-о.)、 Выполните гармонические колебания вокруг точки 0 (рисунок а).
Доска движется в направлении, параллельном оси if, и совершает гармоничное колебание той же частоты вблизи неподвижной точки O. Если закон колебаний доски а определяется уравнением, то определяют абсолютное движение точек/ ВИС. х0 = = в COS (Fi интернет освещенной>)、 ………… Г \ Г \
Смотрите также:
Предмет теоретическая механика

