Кинематические уравнения эйлера
При изучении движения твердого тела, у которого закреплена одна точка, положение такого тела удобно определять специальными углами, называемыми углами Эйлера. Тогда проекции вектора мгновенной угловой скорости вращения твердого тела на оси координат могут быть представлены в зависимости от скоростей изменения углов Эйлера. Рассмотрим движение твердого тела с одной неподвижной точкой. За начало неподвижной системы координат выберем неподвижную точку твердого тела О. Подвижную систему координат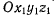 
неизменно свяжем с твердым телом, а начало подвижной системы координат также поместим в неподвижную точку О (рис. 82). Прямую линию, образованную пересечением
плоскостей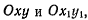 
назовем линией узлов. Положение твердого тела с одной неподвижной точкой определяется положением системы осей, неизменно связанных с твердым телом. Зададим его тремя независимыми параметрами, в качестве которых выберем углы Эйлера.
Обозначим через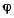 
угол между осью 
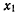и линией узлов, положительное направление угла будем отсчитывать от линии узлов к оси х таким образом, чтобы со стороны положительного направления оси 
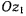оно было бы видно происходящим против хода часовой стрелки. Этот угол 
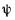будем в дальнейшем называть углом собственного вращения.
Угол 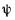между осью х и линией узлов назовем углом прецессии и будем измерять его от оси х к линии узлов так, чтобы положительное вращение было видно со стороны положительного направления оси z происходящим против хода часовой стрелки.
Угол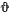 
между неподвижной осью z и подвижной осью 
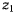будем называть углом нутации и будем измерять его от оси z к оси 
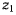так, чтобы положительное вращение было видно со стороны положительного направления линии узлов происходящим против хода часовой стрелки.
Углы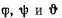 
называются углами Эйлера. Они полностью определяют положение твердого тела. В самом деле, изменение угла 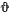определяет отклонение оси 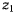от оси z. При постоянном значении угла 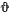ось 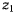может вращаться вокруг оси z. При этом будет вращаться плоскость 
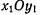и угол прецессии 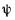будет изменяться. Если же, кроме того, угол прецессии сохраняет постоянное значение, то ось 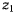будет оставаться неподвижной. Тогда твердое тело будет иметь возможность лишь вращаться вокруг неподвижной оси 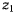В таком движении положение твердого тела будет полностью определяться углом собственного вращения 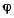В общем случае все три угла 
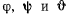могут изменяться одновременно и независимо один от другого.
Мгновенное движение твердого тела определяется бесконечно малыми изменениями углов Эйлера. Пусть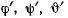 
— скорости изменения углов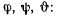 
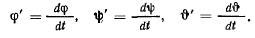
Рассмотрим три вектора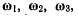 
характеризующие мгновенное движение твердого тела. Вектор 
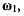направим по оси 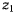в ту сторону, откуда положительное изменение угла 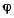видно происходящим
против хода часовой стрелки. Величину вектора выберем равной
скорости изменения угла 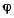Вектор 
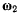направим по оси z в ту сторону, откуда положительное изменение угла 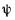видно происходящим против хода часовой стрелки, а величину вектора 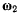выберем равной величине скорости изменения угла 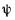Вектор 
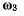направим по линии углов в ту сторону, откуда положительное изменение угла 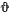видно происходящим против хода часовой отрелки. Величину вектора 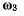выберем равной скорости изменения угла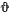
Результирующее мгновенное движение твердого тела можно
представить как сумму трех мгновенных вращений с мгновенными
угловыми скоростями 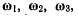а результирующая угловая скорость будет равна
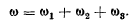
Обозначим через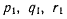 
проекции вектора мгновенной угловой
скорости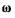 
на подвижные оси 
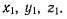Тогда для проекций
получим следующие значения:
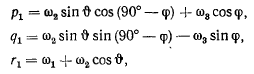
или, подставляя значения величин 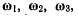будем иметь
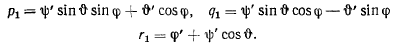
Полученные формулы носят название кинематических уравнений Эйлера.
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
| Распределение ускорений |
| Мгновенный центр ускорений |
| Замечание о конечных перемещениях твердого тела |
| Цели и задачи аксиомы статики |
