Оглавление:




Касательные напряжения в балке двутаврового сечения
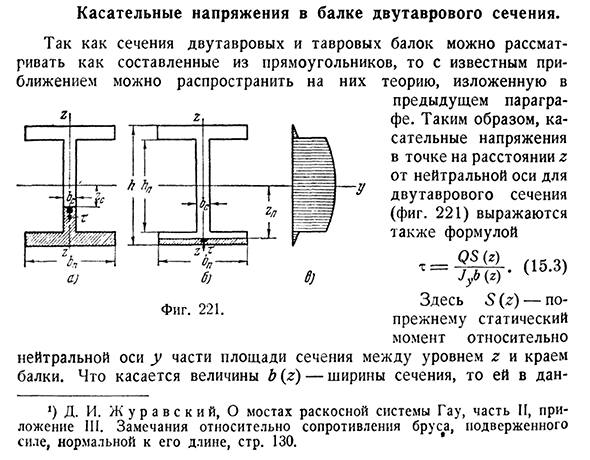
- Касательное напряжение двутавровой балки. Поскольку сечения двутаврового и Т-образного Пучков можно считать состоящими из прямоугольников, то в известном приближении необходимо распространить на них описанную ниже теорию. Фигура. 221 год Предыдущий пункт. Таким образом, тангенциальное напряжение на расстоянии Z от нейтральной ОСИ до поперечного сечения I
балки(рис. 221) также представлена формулой (15-3)) Здесь 5 (g)-неподвижный момент для нейтральной оси в сечении площади поперечного сечения между уровнем z и краем балки. Для величины B (z) — ширина поперечного сечения, она равна Dan-J) D. I. Zh u R равно C K и y, по диагональной системе моста ГАУ,
Часть I, приложение III.§ 92] I-балка 305 с мощностью, нормальной к этой Людмила Фирмаль
длине Это означает, что знаменатель формулы (15.3) следует заменить шириной сечения на уровне Z. Как видно из вывода формулы (15.3), величина b была коэффициентом члена T’b dx, т. е. поперечным размером участка, на котором действует напряжение Tg; следовательно, величина b падает до предела G 221, b), т. е. на платформу, заменяющую ширину BP-пояса-знаменателя. В этом случае выражение (15.3) принимает вид:. _o2l4gp^ Ый h2j в — При расчете тангенциального напряжения на уровне GS
на платформе в стенке необходимо заменить толщину стенки BS вместо SG. Формула также изменена: нам нужно взять статический момент из двух прямоугольников (штриховка на рисунке. 221, а). Когда вы делаете расчет, он выглядит так: ’ТС==’ 8В^[^»/f8LH)+ & СА«(1 фут -)]<15-9) В обоих случаях t изменяется вдоль параболической кривой. Так как толщина стенки двутаврового сечения обычно незначительна, то в этом профиле напряжения сдвига достигают достаточно большой величины, и поэтому
- проверить их невозможно. Среднее значение в Формуле знаменателя (15.9) и может быть заменено на BP и BC. Для величины тангенциального напряжения на этом уровне получены два значения. График распределения напряжений вдоль оси стенки Z-Z принимает вид, показанный на рисунке. 221, А и 222, А. Помните, что это результат расчетов, выполненных в предположении, что формула (15.3) применима к расчету напряжения в точке перехода от пояса к стенке. Более точное исследование показывает, что вдоль линий, совпадающих с осью симметрии поперечного сечения, распределение
касательных напряжений рисуется с достаточной точностью по графику. 222, Б; на линии 2-2, проходящей по самому краю стены, кривая показана на рис. 222, в; на последнем графике показано, что точка входящего угла поперечного сечения напряжения сдвига теоретически достигает очень большого значения; на практике эти входящие Кон 222, г. Максимальная вертикальная координата графика на рисунке. 222, a, b и d приблизительно одинаковы, ссылаясь на точки на нейтральной оси.3 0 6 тангенциальное напряжение балки и главное напряжение [глава XV Поправки не меняют двух основных результатов, вытекающих из графика рисунка. 222, I, то есть: 1)максимальное касательное напряжение находится в
точке нейтральной оси, 2) большая часть боковых сил уравновешивается касательным напряжением стенки. Поэтому использование Людмила Фирмаль
условного графика (рис. 222, а) является действительным. Следует помнить, что это не дает правильного представления о распределении Тангенциальный подчеркивает переход от полки к стене рядом с местом, и внутри самой полки. Результаты исследования распределения напряжений в сечении двутавровой балки позволяют сделать следующие выводы о работе различных элементов этого профиля. Поясная балка, или полка, является самым большим нормальным напряжением, ее ширина велика, а толщина мала, поэтому все они воспринимают те области нормального напряжения, которые близки к самому высокому,
потому что их тангенциальное напряжение очень мало, поэтому пояс принимает относительно небольшую часть силы бокового направления. Напротив, стенка занимает малую часть сопротивления изгибающему моменту, так как ее максимальный размер расположен по высоте и ближе к нейтральной оси, а вертикальное напряжение быстро уменьшается. С другой стороны, величина S (g) при различных значениях z в стенке изменяется незначительно(центральная часть кривой на рисунке). 222, а),
а ширина БС невелика. Таким образом, напряжения сдвига по всей высоте стенок обычно достаточно велики, и почти все поперечные силы уравновешиваются ими. Поэтому в I-м сечении пояс работает в первую очередь для уравновешивания стенки с изгибающим моментом-боковой силой. Проверим касательное напряжение балки, на которую будет действовать поперечная сила Q=2,4 r, [t]=1000 кг / см2. Схематичный профиль двутавровой балки 18 показан на рисунке. 223 момент инерции Jy=1290cm4. Найти касательное напряжение в точках уровня 1, 2, 3. Статические моменты равны:
52=9 • 0,81 • 8,595 =62,6 см, 53 = 62,6 + 0,51 • 8,19 • 4,095 = 79,7 ссылка*.§ 93] касательное напряжение балок круглого сечения 3 07 2400-62, 6 1OP. Два. NW— 1290 — 9 — 2 я не уверен. От 9 до g1CM 2400•79,7. ТЗ-1290 — 0,05 — 2 92 K g1C m ■ обозначает тангенциальное напряжение Обращались в другие подобные Касательное напряжение равно: T1=0, «__2400÷62,6-$кг/см2 2-1290-0,51 г » условный график распределения фиг. 223 Как вы можете видеть, максимальное касательное напряжение намного ниже допустимого напряжения. Это произошло потому, что стены приняли прокатный профиль,
который достаточно толстый. Как мы увидим позже, для композитных балок, заклепок и сварных швов можно добиться большего использования стеновых материалов. По условному графику попробуйте определить долю боковых сил, воспринимаемых стеной. Вертикальная ось графика касательных напряжений умножается на площадь стенки двутавра=Qc 226 • 0,51 • 16,38 с- + (292— 226) — 0,51 • у• 16,38 = 1890 + 4- 368 = 2258 кг составляет 94% от общей силы Q. Метод, приведенный в этом пункте для определения касательного напряжения двутавровой балки, соответствует сечению (полый прямоугольник, Телец и др.).да что с тобой такое?
Смотрите также:

