Оглавление:



Касательные напряжения в балках круглого профиля и пустотелых
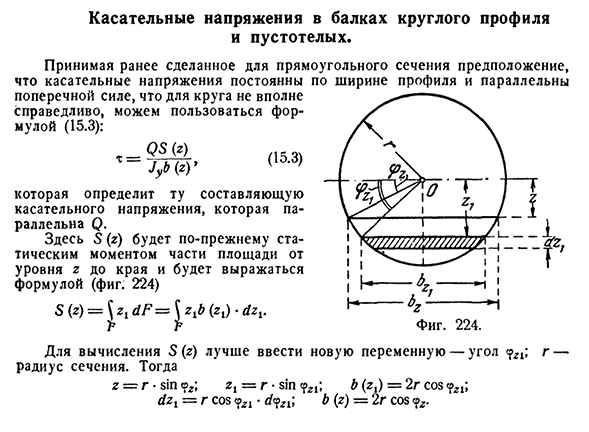
- Круговой профиль балки является полым с напряжением сдвига. Это не так верно для круга, предполагая ранее о прямоугольном поперечном сечении, где касательное напряжение постоянно
по ширине профиля и параллельно боковой силе.): Определить компонент тангенциального напряжения, параллельный qjy b (z)> Где S (g) — статический момент части области от уровня g до
края, выраженный формулой(рис. 224) С(З)=Р! df Для вычисления S (z) Людмила Фирмаль
лучше ввести новый переменный угол g радиуса сечения. Тогда Z=г * грех=г * грех б (ЗТ)=2р с COS(15.7)здесь / y-момент инерции участка трубы; 8T-полукруглый X-статический момент; B — =2T-удвоенная толщина стенки трубы л=т[(’<>+4) — (г » −4)4=(1+4Т) Где Go-средний
радиус трубы. Статический момент полукруга равен разности статического момента относительно диаметра внешнего и внутреннего полукруга.: (15.10)) Необходимые статические моменты полукруга являются Ѕмакс=г[4°+2’)—(г<|-т)]=2Г » 4! 12г?- /Ya2g5* ’ § 94] проверьте прочность основного напряжения 309 И так оно и есть.
- М■2рt_Q_2Q Тмакс-2Т. Реализация ТТК ить~врат выглядит следующим образом: Напомним, что для прямоугольника это соотношение равно 1,5, а для круга-1,33.• 9 • 1 141,4 кг! см П р и М Е вертолета R66. Поперечный изгибающий момент 714=1,2 ТМ и поперечные силы Q=4Т определяют нормальные и тангенциальные напряжения уровня а в нагруженной балке полого профиля балки,
форма поперечного сечения которой показана на рисунке. Двести двадцать пять Момент инерции поперечного сечения Семь. _8 * 14″4•10s, 4•2s J y» T2 ″ 12~» + — = (2 • 7′ −5′ + 1) = 1500 смотреть\ Фигура. Двести двадцать пять Статический момент участка сечения выше уровня ab равен S (z)=2, если можно ожидать
значительных нормальных и тангенциальных напряжений(z=5 см). 8(5+1)=96см*. Людмила Фирмаль
Ширина поперечного сечения (?)Следует принять равной сумме двух стенок b (z)=2+2=4 см толщины. Уровень напряжения АБ: QS (z) _ 4000 * 96Jyb (z)1500 * 4 Mz120000-5, o A»= —— 1500—— = 4 0 0 КЗ! См’ = 64кг! см*
Смотрите также:
| Касательные напряжения в балке прямоугольного сечения (формула Журавского) | Проверка прочности по главным напряжениям |
| Касательные напряжения в балке двутаврового сечения | Направления главных напряжений |

