Оглавление:





Касательные напряжения при изгибе балок тонкостенного профиля. центр изгиба
- Касательные напряжения изгиба балки Тонкостенный профиль. Центр изгиба Коэнзим Q10 НЛ т-р (р±4gp4p Иезекииль. т п ч/дж P/l g0<рис. Триста два НЗ _ Пи! И Если ширина сечения b мала по сравнению с высотой (размером, перпендикулярным нейтральной линии сечения), то предположение, лежащее в основе вывода формулы (10.20), достаточно верно. Таким образом, он показан на рисунке во всех разделах. 302 ширина ТП на уровне, на котором определяется тангенциальное давление, равна y. In в этих случаях схема (10.20) дает правильный результат. Если сечение представляет собой тонкостенный профиль (рис. 302, b, g, 0), то ширина сечения rn^i на полке имеет важное значение и картина распределения
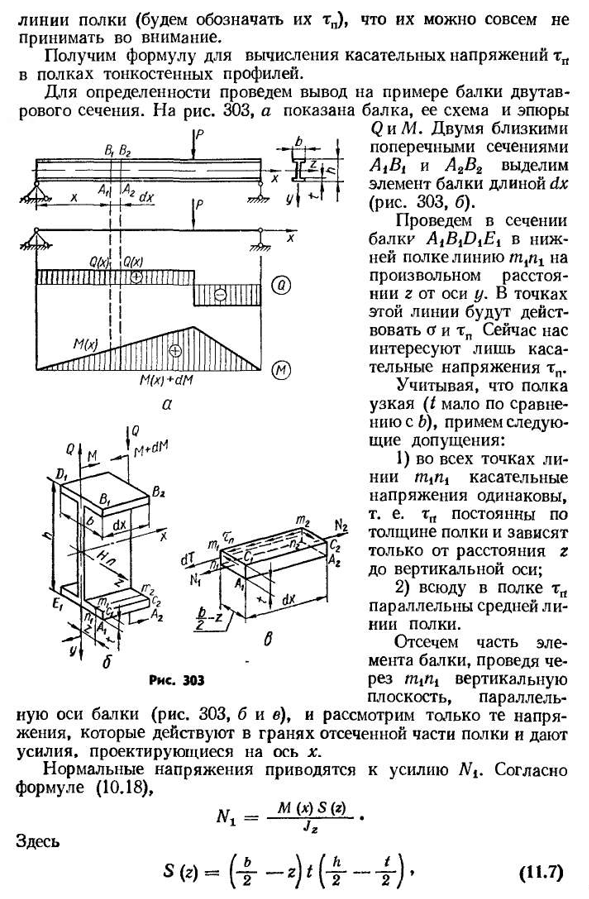
касательных напряжений сильно меняется: они являются не только переменными вдоль центральной линии полки, но и распределением напряжений.、 С Заметим, что на полки действует и тангенциальное напряжение, параллельное Q. Однакоэти напряжения меньше тангенциального напряжения, параллельного среднему 313c Прямой участок. Для риса. 303, а. (Рис. 303, B и C), и Линейные полки (мы показываем их ТП), которые они не могут учесть. Получена формула для расчета тангенциальных напряжений TP в полках тонкостенных профилей. Действительно, мы делаем выводы о примере балки I-beam, ее схеме и диаграммах Q и M. два более близких участка t Bt и A2B2, выделяют элементы длины балки
dx 303, b). В точке этой линии o ’ проведите линию к сечению балки aibidiei Людмила Фирмаль
нижней полки на любом расстоянии z от оси y, действует TP. Теперь нас интересует только касательное напряжение TP. Учитывая, что папка узкая (я маленький по сравнению с b), примите следующее предположение:1) во всех точках линии касательное напряжение одинаково, то есть толщина папки фиксирована. Прорежем некоторые из балочных элементов, выполненных через вертикальную плоскость митии, параллельно * * рассмотрим тапко их напря-дадим отрезную часть полки. ось луча, действующая на грань силы, проецируется на ось X. Нормальное давление в силу НЗ. По формуле(10.18), Здесь. в _AIW С(З) / В1 ″ Тг д)-(11.7)4 314t. E. S (z) — статический момент области a&t^относительно нейтральной линии. Это функция координаты G. На поверхности ags2tt2p2,
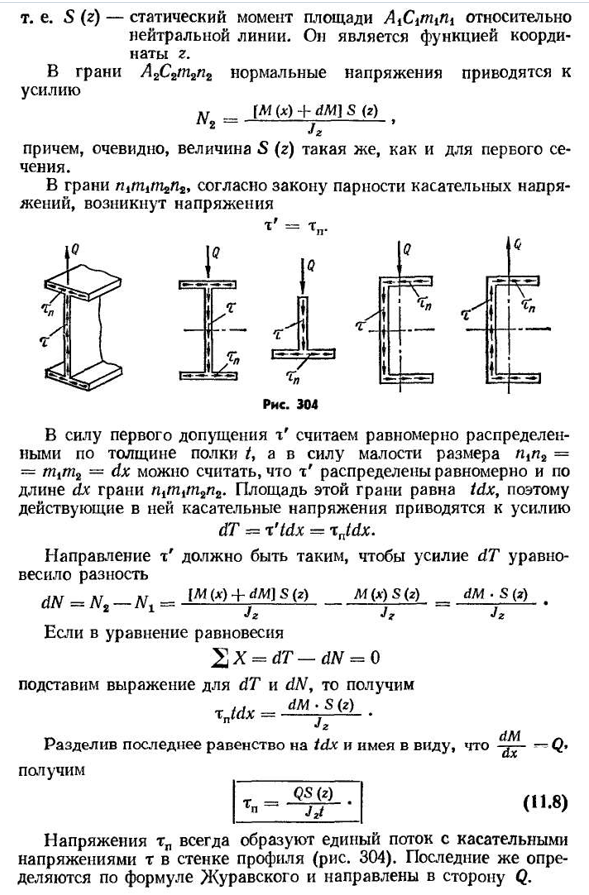
нормальное напряжение тока уменьшено к силе V (м (Х)+СД) с (г)—J в’ J2 в И, по-видимому, значение S (g) такое же, как и в первом разделе. В забое по закону пары касательных напряжений возникает напряжение Триста четыре риса Благодаря первому предположению g ’мы рассматриваем равномерное распределение по толщине полки/, из-за малости размера p1p2==t^T2-dx мы имеем равномерное распределение T’. м им (*)+<•м]ы(З)М(Л)С(З)ДМ * с(з)Л1-j2Jz~ЮЖД’ Направление t ’ должно быть таким, чтобы сила dT уравновешивала разность dN-Ns% X=dT-dN=0, где rntdx=получается при подстановке формул dT и dN. Разделите последнее равенство на Tdx и имейте в виду, что мы получаем Стенка профиля давления TA (рис. Тангенциальное давление t образуют единый поток всегда 304).
- Последнее определяется формулой Журавского и направлено на Q. 315 уравнение (11.8)формула TP и тангенциального напряжения в полках для тангенциального напряжения (10.20) t в стенках позволяет рассчитать тангенциальное напряжение любого из тонкостенных профилей, поэтому, как правило, двутавры и каналы игнорируют смещение полок и считают, что полки имеют заданную постоянную/толщину марок. Кроме того, если игнорировать кривую, то участок t подводится к полке, а участок TP-к оси профиля, игнорируя наличие стенок. Рис триста пять ^!кгс / см?- Один. Пример 48. Двутавровая балка № 20 строит полную диаграмму касательных напряжений для поперечного сечения, боковая сила Юд7кгс/см2 Q=10 000кгф (рис. 305). Из ассортимента находим/= = 1840cm4; S=104cm3 и вычисляем статический момент полки относительно нейтральной линии: 4-4-4)= =10 • 0,84 —— СМ1=80,47 СМ9. Q «Колыбель» Тогда касательное
напряжение на стыке стенки и полки _Opolki_10 000■80,47 2_m J, 2 1~J4 ~ 1840■0,52’~841′ А максимальное касательное напряжение в точке нейтральной линии t QS 10 (XX) −104,. / L около 7, t-Max= — 7g=-1840. o -; 52-кгс / см=1087 кгс/см-по этим данным строят параболический график t стенки. Чтобы построить график тангенциального напряжения TP на полке двутавровой балки, обратите внимание на то, что согласно формулам (11.7) и (11.8), ’)• Поскольку z-Координата точки, в которой определяется TP, содержится в этом уравнении первого порядка, график TP становится прямой линией. Прямой расчет осуществляется по формуле (11.8). Для края полки 0, поэтому TP=0. Примерно в середине полки (g= = 0) ТП Q Один. [B \2 2/до 2 5 (0)=~5 полок=4 0,2 см’ ; С ре о » К. Р10, 000-40. 2,. о й л,. 1840 7o, 34-KGS / CM=260KGS / CM • Четыре» На основании этих данных
мы создаем треугольный участок TP в правой половине полки. Потому что Людмила Фирмаль
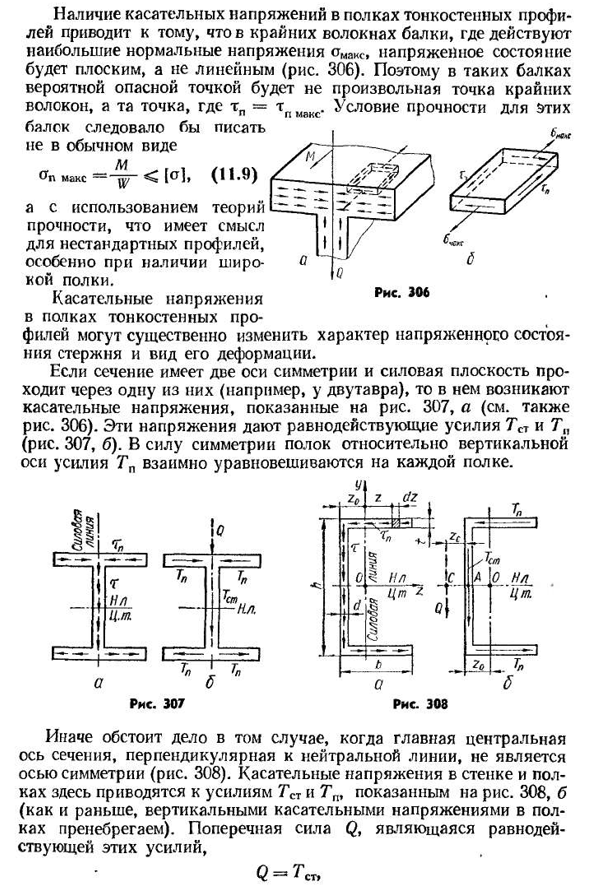
статический момент абсолютной величины такой же, как и у правой половины полки. Очевидно, такого же рода сюжет имеет ТП и для нижних полок, Триста шестнадцать, Наличие касательных напряжений на полках тонкостенных профилей приводит к тому, что крайние волокна балки, где максимальные вертикальные напряжения OMAC (., Напряженное состояние является линейным, а не плоским(рис. 306). Таким образом, в таком пучке возможная опасность находится не в любой точке крайнего волокна, а в точке TP=TP max. Условия интенсивности этих лучей не должны быть записаны в обычной форме. Макс= — ^г<[о], (11.9) Причем с использованием теории прочности, что имеет смысл для нестандартных профилей, особенно при наличии широких полок.
Механические напряжения на полках тонкостенных профилей могут существенно изменить напряженное состояние стержня и характер его деформации. Если сечение имеет две оси симметрии и силовая плоскость проходит через одну из них(например, в двутавровой балке), то на ней возникает тангенциальное напряжение, показанное на рисунке. 307, и(см. Также рисунок. 306). Эти напряжения дают результирующую силу 7ST и 7YA(рис. 307, б). Благодаря симметрии полок по отношению к вертикальной оси, силы трения взаимно уравновешиваются на каждой полке. Но 1<3 4!% Т / / / 7 Рис 307фиг. Триста восемь В этом случае главная центральная ось сечения, перпендикулярная нейтральной линии, не является
симметричной(рис. 308). Тангенциальное напряжение стен и полок сводится к силе TST и TP, как показано на рисунке ниже. 308, b (как и прежде, вертикальное касательное напряжение полки игнорируется). Боковая сила Q которая является результатом этих сил, М= * Ст Т, 317 четко направлена вниз вертикально, но она не проходит через поперечное сечение центра тяжести, так как уже две силы ТП все же дают и пару сил. Сила Q сдвигает на некоторое расстояние zc (рис. 308, Б), пересекают нейтральную линию с С. Чтобы найти Zc, используйте тот факт, что результирующий момент для любой точки равен сумме моментов компонентов для одной и той же точки. Вычислите момент для точки C. Затем получать
2mc=м(ЗЦ+а)_T11(/1_0=о, Откуда zg=(L— 0 —- • O* —®) эта формула еще не дает окончательного ответа на вопрос о расположении точки C, так как она представляет координаты zc не только по геометрическим, но и по силовым факторам. Чтобы исключить последнее, рассчитайте силу TP. Элементы полки dz(рис. 308, а) действует базовая сила dTn=xntdz. И так оно и есть., Б-Н Т а-т ф Р » ДЗ. — (G0-то д) Чтобы использовать выражение (11.8), используйте _QS (g)rt~L И я думаю, что С (З)=(Б-г) / , получить 7’с=Щ — ^в±Ф(6_Zo_z) ДЗ= — (З0-Д)6-З0 — (З0-д) Добавление последнего результата к выражению (11.9) в конечном итоге даст t — (b-d)*4J Д2 (11.10)) Посмотрим, какова величина
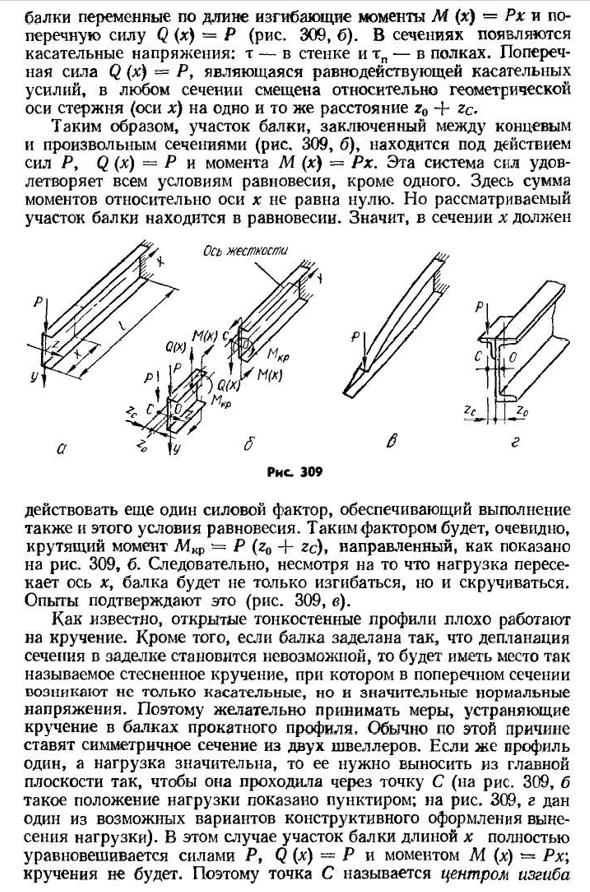
смещения Q результата относительно центроида сечения. Чтобы быть ясным, секция канала консоли имеет вертикальную нагрузку P(рис. 309, а), причем силовая плоскость совпадает с одной из двух главных плоскостей стержня (плоскость XY). Это усилие будет в разделе 318b имеет изгибающий момент переменной длины M (x) — Px и поперечную силу Q(x)=P(фиг.309, б). Имеются касательные напряжения в сечениях: Т-стенка и тп-на полках. Боковая сила Q (x)-P, являющаяся результатом действия тангенциальной силы, смещается на одинаковое расстояние z0+zc относительно геометрической оси стержня (оси x). Таким образом, поперечное сечение (рис. 309, б) под действием силы P, Q(x)-P p, M(x)=Px. Эта система сил отвечает всем
равновесным состояниям, кроме одного. Здесь сумма моментов для оси x не равна нулю. Но та часть луча, о которой идет речь, находится в равновесии. Значение, должно быть в разделе x Рисунок 309 Точно так же существует еще один силовой фактор, обеспечивающий выполнение этого состояния равновесия. Такими факторами, по-видимому, будет крутящий момент L4kr-P (z0-|-zc), как показано на рисунке. Так, несмотря на то, что груз пересекает ось Х, балка не только изгибается, но и закручивается. На рисунке 309, подтвержденном экспериментами).
Смотрите также:
| Расчет на действие сил инерции при изгибе | Основы расчета балок на упругом основании |
| О расчете составных балок | Изгиб балок, материал которых не следует закону гука |

