Оглавление:






Касательные напряжения при изгибе балки
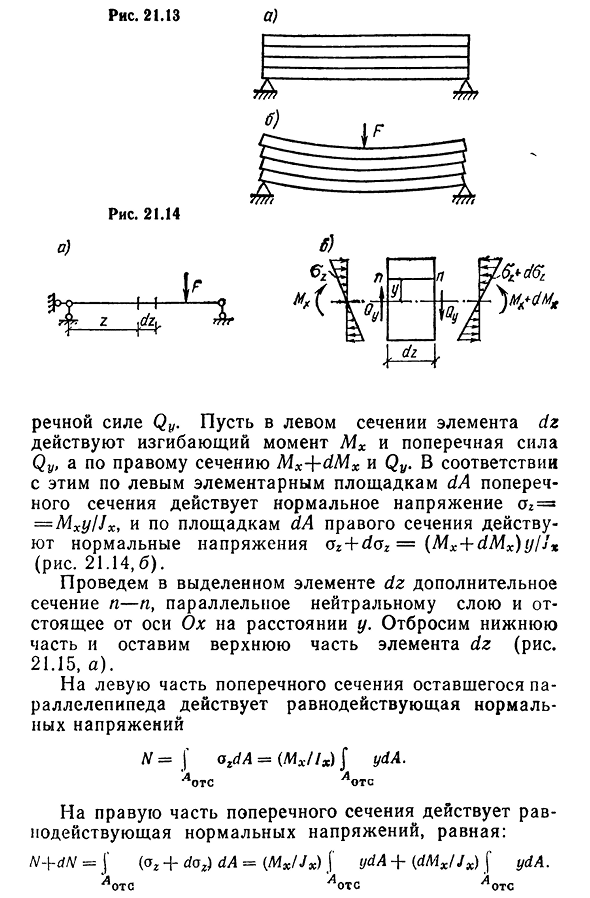
- В отличие от чистого изгиба при прямом поперечном изгибе в поперечном сечении тангенциального напряжения балки при изгибе балки, помимо изгибающего момента, существует также поперечная сила. Исходя из пары касательных напряжений, они также возникают в поперечном сечении параллельно нейтральному слою балки, в котором продольные волокна смещаются относительно друг друга в продольном направлении. Это легко видно на примере гибочных балок, состоящих из множества отдельных слоев. После преодоления силы трения отдельные слои перемещаются, как показано на
рисунке. 21.13, б. В результате сдвиговой деформации поперечное сечение слегка искривлено, что нарушает гипотезу о плоском сечении при поперечном изгибе. Однако эта ситуация мало влияет на распределение и величину нормального напряжения, поэтому гипотеза плоского поперечного сечения считается справедливой для поперечного изгиба, а вертикальное напряжение составляет 21.14, а), бесконечно малый элемент длины dz.
Тангенциальная нагрузка не прикладывается к боковой поверхности, поэтому тангенциальное давление контура поперечного сечения может быть направлено так, Людмила Фирмаль
чтобы быть в контакте с ним или равным нулю, в то время как тангенциальное напряжение прямоугольного сечения будет параллельно папе.- 226 страниц. 21.13 в) В левом сечении элемента DZ момент MX и боковая сила Речной силы Qy. Пусть qy действует изгибом, а на правом участке Mx+dMx и Qy. В зависимости от этого, нормальное напряжение О2= = MxylJx действует на базе сайта да слева от сечения,а нормальные напряжения аз+д(5з=(МХ+расширения интеллектуального анализа данных) г/JX у актов на сайте в правой части(рис. 21.14, б). Проведем с выделенными элементами DZ
дополнительный разрез n-n, параллельный нейтральному слою и отстоящий от оси o на расстояние Y. снимем нижнюю часть и верхнюю часть элемента dz 21.15, а). На левую сторону поперечного сечения оставшегося параллелепипеда влияет результат нормального напряжения=J’otda=(Mx/Ix)f ydA. ^ЗТ^ЗТ Справа от сечения зависит от нормального напряжения результат равен:а/|/ — п/в-|(А2+доз) да=(ТХ/JX используется)[ыда-Джей(расширения интеллектуального анализа данных/JX используется)(ыда. ОТС л ОТС л ОТС Пятнадцать.* На левой и правой частях остальных элементов dz возникает тангенциальное напряжение вдоль оси операционного усилителя,
- величина которого зависит от высоты сечения. Показывает значение напряжения сдвига в точке под платформой p-p\и p-P2-t2up. Исходя из закона парного касательного напряжения’изин^^yzn, такое же касательное напряжение действует и на область под плоскостью поперечного сечения nniiti2, результат которого обозначен г. Из условия равновесия S z=0 для остатка элемента dz получаем T — ±N-N-dN-O, откуда T — =dN=(dM x/Jx)\ydA. ^OTS, где Sotc=J ydA представляет собой статический момент AOTS отрезанной части участка l0ts поперечного сечения относительно нейтральной оси ox(рис. 21.15, 6). Затем T=dMx S0TC / J x. (21,6) Из этого состояния невозможно
установить величину касательного напряжения и закон его изменения, который зависит от формы поперечного сечения. Прямоугольное сечение. Для прямоугольного поперечного сечения предположим, что напряжения сдвига равномерно распределены по ширине поперечного сечения и изменяются только по высоте. Тогда поперечная сила t=J^n d2by’ Где U-ширина участка на расстоянии y от нейтральной оси (A. представляет собой значение T в выражении 228 (21.6) х zyn Д з Г Б М=д М Х S или J х или Х zyn(д М Х ЛД З) (С О^/Ч y1L Как DMx/d z=Q y, мы получаем H = %M (217) Полученная формула для расчета касательного напряжения при изгибе балки называется формулой Журавского.
Построим график касательного напряжения на балке прямоугольного сечения высотой h и шириной B. осевой Людмила Фирмаль
момент инерции прямоугольного сечения к оси ox равен Jx=bli3 / 12\ ^ЗТ=^ОЦ!/s>где Lote-область отрезанной части сечения, а us-расстояние от центра масс области отрезанной части до нейтральной оси ox. В этом примере Величина тангенциального напряжения hgup на участке на расстоянии y от оси Ah: = QyS0TC=^1 2 (t-^)\^u n ‘ bJx bh32b bh3\4 / Из полученного уравнения видно, что тангенциальное напряжение по высоте поперечного сечения изменяется по закону вторичной параболы в прямоугольном сечении с постоянной величиной ширины поперечного сечения B. В крайних точках Y=±h) 2tz1/=0. Максимальное напряжение сдвига возникает при Y=0 на нейтральной оси поперечного сечения. Цаиб = SQy!2bh. Схема
тангенциального напряжения показана на рисунке. 21.15, V. Мы здесь, чтобы помочь вам.Закон изменения касательного напряжения для высоты поперечного сечения зависит не только от изменения S0Tc, но и от изменения ширины поперечного сечения. 229двутавровое отделение. Поскольку поперечное сечение двутавровой балки имеет резкое изменение ширины на границе раздела вертикальной стенки двутавра с горизонтальными полками и накладывает дополнительные особенности на распределение касательных напряжений, то тангенциальные напряжения в стенке и полке
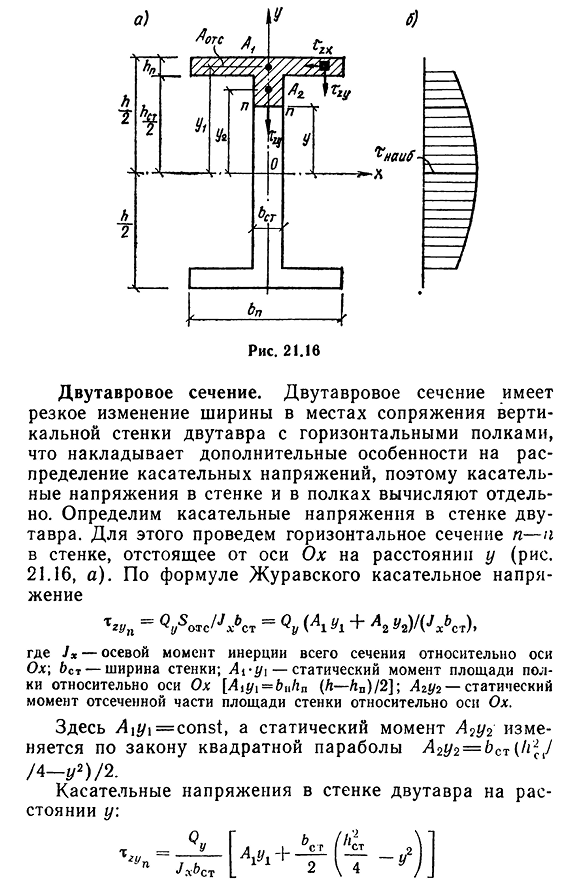
рассчитываются отдельно. Определено касательное напряжение в стенке двутавровой балки. Для этого нарисуйте горизонтальный участок р-р на стене. 21.16, а). По формуле Журавского касательное напряжение T^n=Q и^L t= % (L1U1+2-осевой момент инерции всего участка вокруг оси ox-LSC-ширина; и^y\ — статический момент площади полки относительно оси Ox[_Aiy\ = buhn (h / PG)/2]; 対2θ 2 Здесь a=const, а статический момент A2u2 изменяется в соответствии с параболой квадрата, A2y2=bCT (h jj/4-y2)/2. Встаньте по касательной: n= — J — — — — — — — — — I»g»77″ I —— — икс bCT L2\4 Напряжение на стенках двутавровой балки на шнурке- % б р р 230 или X7f! = g u p J Крист Если у вас есть — %zy-Qybuhn(h-hn) / 2JxbcT’ При Y=0 тангенциальное напряжение достигает гораздо большего значения: * iaib=(W [(V n / 2) (l-M+6t и STL / 8]. Схема тангенциального напряжения в стенке двутавровой балки показана на рисунке. 21.16, б График
тангенциального напряжения вдоль высоты стенки двутавра изменяется по закону вторичной параболы, но в отличие от прямоугольного сечения в крайней точке стенки тангенциальное напряжение равно нулю. Максимальное касательное напряжение возникает на нейтральной оси двутавра. Теперь давайте сосредоточимся на касательном напряжении двутавровой полки. Каждая точка двутавровой балки имеет два касательных напряжения, xzy и T2x. 21.16). Вертикальное касательное напряжение T2?/Не может быть определен методом сопротивления материала полкам, и для их изучения необходимо включить более строгий метод теории упругости. В связи с тем, что эти касательные напряжения
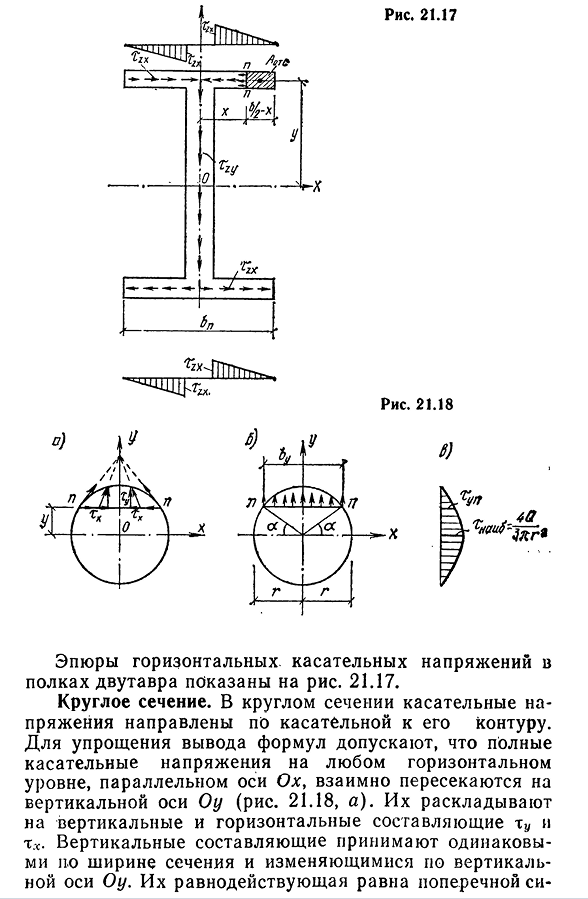
мало влияют на прочность балок, их значениями пренебрегают. Тангенциальное давление T2X горизонтальной стойки равномерно распределено по толщине стойки и направлено в противоположном направлении от оси операционного усилителя. Их результатом является самобалансированная система сил(рис. 21.17). В практических расчетах величина горизонтального касательного напряжения определяется по формуле Журавского. В этом случае отсекают участок полочной площади, текущий вертикальный участок р-р от края полки(фиг. 21.17). Статический момент отрезанной части площади рассчитывается для оси двутавровой
балки(рис. 21.17): «$OTS=x) y. Тогда величина напряжения сдвига xZXn в сечении n-I: =V o r c / ^a=W2-y / J*> Где y=(h-hn)/2. 231 страница. 21.17 Рис 21.18 Фигура горизонтального касательного напряжения в полке двутавровой балки показана на рисунке. 21.17. Круглое сечение. В круговом сечении касательное напряжение направлено по касательной к его контуру. Для упрощения вывода уравнения полные касательные напряжения на любом горизонтальном уровне, параллельном оси Oh, должны пересекаться друг с другом на вертикальной оси Oh(рис.21.18, а). Они разлагаются на вертикальные и горизонтальные составляющие, т. Предполагается, что вертикальная составляющая имеет одинаковую ширину сечения и
изменяется вдоль перпендикулярной оси операционного усилителя. Их результат равен поперечному si- 232. Используя формулу К. Ю. Журавского, находим закон изменения ^Up=4Qy (r2 — * / 2) / Zlg4. Максимальное значение Tu происходит на уровне горизонтального диаметра y=0: TZ / max-4<2U / 3lg2. Горизонтальная часть Th-это взаимно уравновешенное давление. В горизонтальном диаметре он равен нулю и не влияет на прочность балки. Эта цифра показана на рисунке. 21.18, ст.
Смотрите также:
Решение задач по технической механике

