Оглавление:



Касательные напряжении при изгибе в плоскости симметрии
- Касательное напряжение изгиба в плоскости симметрии. Если внешняя сила действует на плоскость симметрии сечения, которую мы принимаем за плоскость UOG, то в Формуле (126.4) остается один член: Т. 6= — ^p6d s. (127.1) X o Выражение (127.1) иногда используется
для непрерывных сечений, которые предполагают, что вектор t параллелен оси y и что B понимает ширину сечения на расстоянии’y от оси X. Эти гипотезы принимаются с большим доверием. Кстати, их точное решение не подтверждается.
Недопустимость допущения Людмила Фирмаль
параллельности векторов t «оси y и C» обнаруживается из теоремы§ 89, где касательный вектор напряжений контактирует с контуром в точке контура. Формула ухода Diaco, solid или cocotteenage (127.1) для прямоугольных секций является правильной. Здесь надо взять(рис. Сто девяносто.): б=у^=4 [ / £ ], •И (127.2)
Тангенциальное напряжение в Д. И. Журавский(1855) Рис, 191. г » х ___ Около Один. Четыре. Изгиб и кручение 278 тонкостенных стержней[гл.» График распределения касательных напряжений в поперечном сечении представляет собой параболу. 190);
- максимальное напряжение получается на нейтральной оси PRN j=0, а величина его т. __3Qy Т Макс 2bh • Здесь Qyjbh представляет собой силу резания, деленную на площадь, то есть среднее напряжение. Первоначально считалось, что изгиб применяется для расчета деревянных «балок», которые имеют небольшое сопротивление сколам и касательным. Стресс также должен быть рассмотрен для массивного про Филей. Полученное решение является убедительным. Проблема заключается в том, что наибольшее касательное
напряжение и наибольшее вертикальное напряжение возникают в разных точках поперечного сечения, т и о являются наибольшими. t=0, и наоборот. В тонкостенных стержнях дело может обстоять иначе, как видно из приведенного ниже примера расчета двутавровой балки. Предположим, что размеры B и h намного больше, чем 6t(рис. 191). Вычислите статический момент / затененного участка, который определяет тангенциальное напряжение
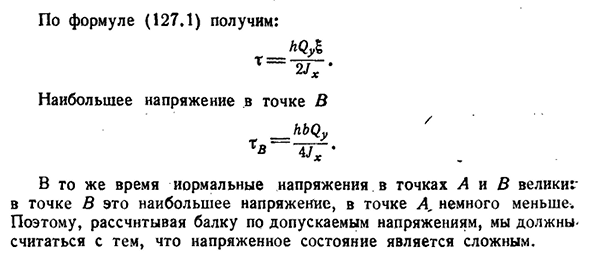
стенки.:/ в p^=4 м. +4 (t -/) \ — I Согласно формуле (127.1) — Ф. Наибольшее Людмила Фирмаль
тангенциальное давление получается в середине стенки, но в точке А оно все равно довольно значительное: AWjQj, При применении формулы (127.1)к полке необходимо найти статический момент затененной части фигуры относительно оси X. Этот момент,§ 128]центр изгиба Получено по формуле (127.1): штаб£ Максимальное давление на точки — hbQy Я J х В Д • В то же время нормальное напряжение в точке A и в точке B больше в точке B, которая является самым высоким напряжением в точке A и немного меньше. Поэтому для расчета балок допустимых напряжений необходимо учитывать тот факт, что напряженное состояние является сложным.
Смотрите также:
| Изгиб балки на упругом основании | Центр изгиба |
| Нормальные и касательные напряжения при изгибе | Дополнительные напряжения при кручении |

