Оглавление:
Касательная плоскость и нормаль к поверхности
Рассмотрим одно из геометрических приложений частных производных функции двух переменных. Пусть функция  дифференцируема в точке
дифференцируема в точке 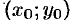 некоторой области
некоторой области 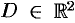 . Рассечем поверхность
. Рассечем поверхность  , изображающую функцию
, изображающую функцию  , плоскостями
, плоскостями 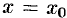 и
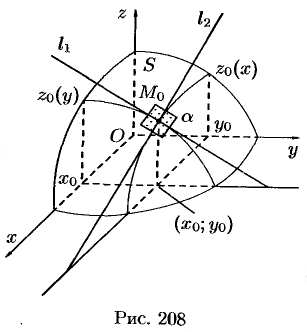
и  (см. рис. 208). Плоскость
(см. рис. 208). Плоскость 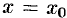 пересекает поверхность
пересекает поверхность  по некоторой линии
по некоторой линии 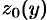 , уравнение которой получается подстановкой в выражение исходной функции
, уравнение которой получается подстановкой в выражение исходной функции  вместо
вместо  числа
числа  . Точка
. Точка  принадлежит кривой
принадлежит кривой 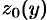 . В силу дифференцируемости функции
. В силу дифференцируемости функции  в точке
в точке 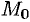 функция
функция 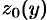 также является дифференцируемой в точке
также является дифференцируемой в точке  . Следовательно, в этой точке в плоскости
. Следовательно, в этой точке в плоскости 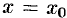 к кривой
к кривой 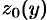 может быть проведена касательная
может быть проведена касательная  .
.
Проводя аналогичные рассуждения для сечения  , построим касательную
, построим касательную  к кривой
к кривой 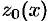 в точке
в точке 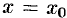 . Прямые
. Прямые  и
и  определяют плоскость
определяют плоскость 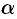 , которая называется касательной плоскостью к поверхности
, которая называется касательной плоскостью к поверхности  в точке
в точке 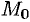 .
.
Составим ее уравнение. Так как плоскость а проходит через точку 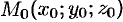 , то ее уравнение может быть записано в виде
, то ее уравнение может быть записано в виде
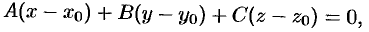
которое можно переписать так:
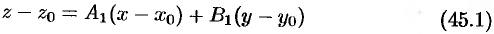
(разделив уравнение на 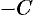 и обозначив
и обозначив  ).
).
Найдем 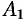 и
и 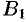 .
.
Уравнения касательных  и
и  имеют вид
имеют вид
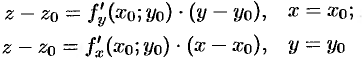
соответственно.
Касательная  лежит в плоскости
лежит в плоскости 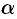 , следовательно, координаты всех точек
, следовательно, координаты всех точек  удовлетворяют уравнению (45.1). Этот факт можно записать в виде системы
удовлетворяют уравнению (45.1). Этот факт можно записать в виде системы
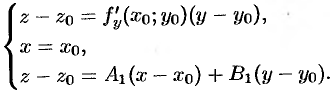
Разрешая эту систему относительно 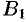 получим, что
получим, что 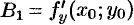 .
.
Проводя аналогичные рассуждения для касательной  , легко установить, что
, легко установить, что  .
.
Подставив значения 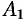 и
и 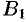 в уравнение (45.1), получаем искомое уравнение касательной плоскости:
в уравнение (45.1), получаем искомое уравнение касательной плоскости:
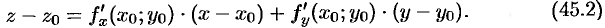
Прямая, проходящая через точку 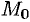 и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется ее нормалью.
и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется ее нормалью.
Используя условие перпендикулярности прямой и плоскости (см. с. 103), легко получить канонические уравнения нормали:
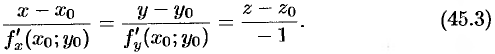
Если поверхность  задана уравнением
задана уравнением 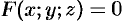 , то уравнения (45.2) и (45.3), с учетом того, что частные производные могут быть найдены как производные неявной функции:
, то уравнения (45.2) и (45.3), с учетом того, что частные производные могут быть найдены как производные неявной функции:
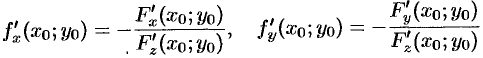
(см. формулы (44.12)), примут соответственно вид
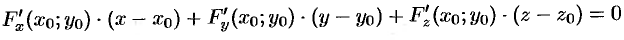
и
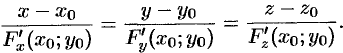
Замечание. Формулы касательной плоскости и нормали к поверхности получены для обыкновенных, т. е. не особых, точек поверхности Точка 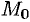 поверхности называется особой, если в этой точке все частные производные равны нулю или хотя бы одна из них не существует. Такие точки мы не рассматриваем.
поверхности называется особой, если в этой точке все частные производные равны нулю или хотя бы одна из них не существует. Такие точки мы не рассматриваем.
Пример №45.1.
Написать уравнения касательной плоскости и нормали к параболоиду вращения 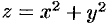 в точке
в точке  .
.
Решение:
Здесь 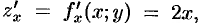
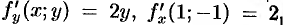
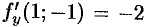 . Пользуясь формулами (45.2) и (45.3) получаем ура некие касательной плоскости:
. Пользуясь формулами (45.2) и (45.3) получаем ура некие касательной плоскости:  или
или  и уравнение нормали:
и уравнение нормали: 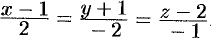 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Инвариантность формы полного дифференциала |
| Дифференцирование неявной функции |
| Необходимые и достаточные условия экстремума |
| Наибольшее и наименьшее значения функции в замкнутой области |

