Касательная к кривой
Дадим сначала общее определение касательной к кривой.
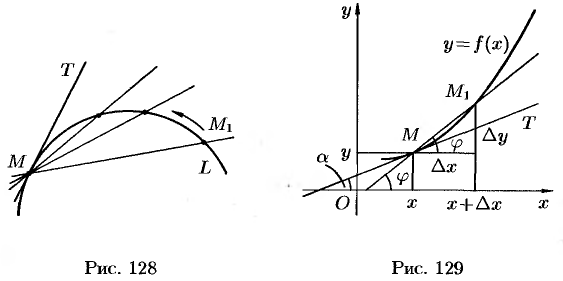
Возьмем на непрерывной кривой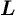 
две точки 
и 
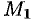(см. рис. 128).
Прямую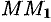 
, проходящую через эти точки, называют секущей.
Пусть точка 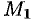, двигаясь вдоль кривой 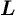, неограниченно приближается к точке . Тогда секущая, поворачиваясь около точки , стремится к некоторому предельному положению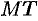 
.
Касательной к данной кривой в данной точке называется предельное положение 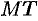секущей 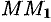, проходящей через точку , когда вторая точка пересечения 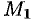неограниченно приближается по кривой к точке .
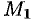Рассмотрим теперь график непрерывной кривой 
, имеющий в точке 
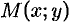не вертикальную касательную. Найдем ее угловом коэффициент 
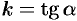, где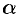 
— угол касательной с осью 
.
Для этого проведем через точку и точку 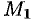графика с абсциссой 
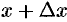секущую (см. рис. 129). Обозначим через 
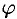— угол между секущей и осью . На рисунке видно, что угловой коэффициент секущей равен
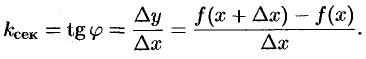
При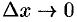 
в силу непрерывности функции приращение 
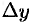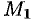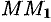тоже стремится к нулю; поэтому точка неограниченно приближается по кривой к точке , а секущая , поворачиваясь около точки , переходит в касательную. Угол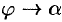 
, т. е. 
.
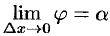Следовательно,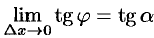
.
Поэтому угловой коэффициент касательной равен
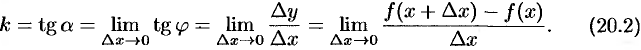
К нахождению пределов вида (20.1) и (20.2) приводят решения и множества других задач. Можно показать, что:
- если
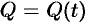— количество электричества, проходящего через поперечное сечение проводника за время 
, то сила тока в момент времени равна
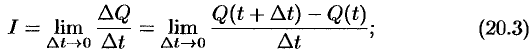
- если
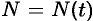— количество вещества, вступающего в химическую реакцию за время , то скорость химической реакции в момент времени равна
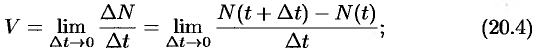
- если
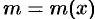— масса неоднородного стержня между точкам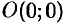и 
и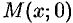 
, то линейная плотность стержня в точке 
есть
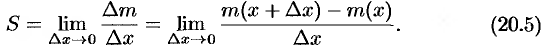
Пределы (20.1) (20.5) имеют одинаковый вид; везде требуется найти предел отношения приращения функции к приращению аргумента. Этот предел называют производной. Эти пределы можно записать так:
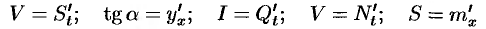
(читается «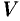
равно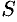 
штрих по », «тангенс 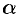равен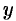 
штрих по » и т. д.).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Свойства функций, непрерывных на отрезке |
| Скорость прямолинейного движения |
| Связь между непрерывностью и дифференцируемостью функции |
| Производная суммы, разности, произведения и частного функций |
