Касательная и нормаль

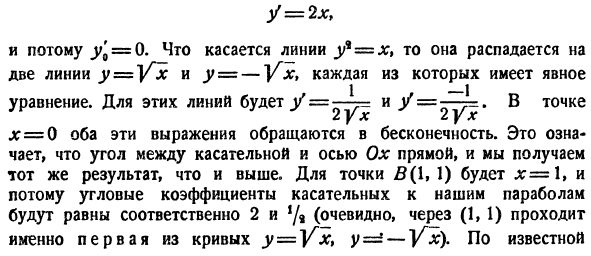
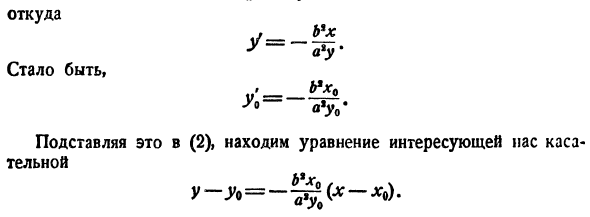
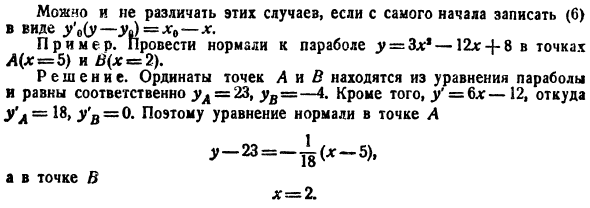
Касательная и нормаль

• Касательные и нормальные Н°1.Сохраняет касательные. Аналитическая геометрия ставит задачу изучения геометрических задач с использованием вычислительных средств. Однако сфера применения этих инструментов была весьма ограничена и ограничивалась базовой алгеброй и тригонометрией. Более

продвинутая область математики, которая занимается решением исчислением, называется дифференциальной геометрией. Наложите только самую простую информацию из этой области, но все же ограничьте ее только геометрией на плоскости. Если вам нужно использовать производные (различного порядка) рассматриваемых функций,

геометрических задач с дифференциальным Людмила Фирмаль

вы всегда можете использовать производные всех/ ’（） «/»（）> (0> psf и так далее существуют, непрерывны. Во-первых, давайте рассмотрим проблему рисования касательной к кривой г ^ Ф(Х) (1） Кривая(!В точке M (x & y0) выше. n°1§ 1 гл. III, кстати, учитывая определение самой касательной, я обнаружил, что угловой коэффициент рассматриваемой касательной равен/’ (•).То есть это значение

ординатной производной для абсциссы, вычисленной при x = x0i t. то есть абсцисса точки контакта).Предполагая краткость f (x0)= y ’ {t, получаем уравнение касательной линии. Г-е= уя (х- ’ хо)’(2） Образцы. 1) Нарисуйте касательную к кривой y = Inx на пересечении кривой и оси Ox. Решение. Касательная точка должна быть y = 0.полагая АО=== = = 0, будет х = 1.Так, точки касания будут М(1,

• 0).Также откуда y ’ 0 =1.Таким образом, уравнение касательной г-х-1. 2) Найти точку кривой y = 2x * — bx — \ — где касательная параллельна прямой y = bx — \ — 11. Решение. Угловой коэффициент касательной равен y = 4×0-5, где x0-абсцисса точки контакта. С другой стороны, наклон этой прямой линии равен 3.И так оно и есть.、 4lg0-5 =

3 откуда jc0 = 2.In в этом случае уравнение кривой равно^ 0 = −1.Таким образом, искомая точка будет равна (2, −1). 3)под каким углом парабола пересекается) y = x и y * = x? Решение. Парабола пересекается в точке A (0, 0)、 £(1, 1). в точке A (0, 0) касательными парабол y = xh и uh = x являются оси Ox и оси Oy, respectively. So, в этой точке

На первой строке рассматриваемой строки Итак, y0 = 0.As Людмила Фирмаль

параболы пересекаются под прямым углом. Этот результат также может быть получен с помощью выражения (2). для строки y * = x она разделена на 2 строки y = — \ Tx и y = — Yx, каждая из которых имеет явное equation. In эти строки есть у Ат x = 0 оба этих выражения

бесконечны. Это означает, что угол между касательной и осью Ox является прямой линией, и мы получаем тот же результат, что и выше. Точка Z? Так как (L, 1) равно x-1, то угловые коэффициенты тангенса параболы равны 2 и 2 соответственно!/ Будет равно 9 (очевидно, кривая y = Yx, — yx сначала проходит (1,1))) От меня

формула у% −1? * П В точке M (x0, y0) над этим эллипсом. Решение. Выражение (3) является неявным выражением. Он разделен на 2 явных уравнения (3） (4 )） Во 2-м случае нужно выбрать 1-й. Л <0.Если вы сделаете это, вы можете использовать формулу (2).Вместо этого приведите еще один весьма информативный

аргумент. Это хорошо относится к кривой, заданной неявным уравнением. То есть, если вы найдете явное выражение от (3) до x (которое будет 1 из Формулы(4), но сейчас это не важно) и присвоите результат (3), результирующая связь станет идентичностью (по отношению к x).Запишите это удостоверение еще раз в форме (3).Это означает функцию x, которая получается путем решения

выражения*) (3) в y. мы хотим дифференцировать это тождество относительно x и (y * y = 2yy \ И ’B%’ Откуда год^- Так… Вау.* Подставляя это в(2), Находим искомое уравнение Отсюда ■У-Уд -.УО _x * — xx9 б*«? ’ Или ХХ * Луу * \ У1 «Б5» Точка Л/(*о, jo) находится на эллипсе (3), поэтому правая сторона (5) равна 1, и, наконец, Если читатель использует тот же метод, уравнение Xya V1 Касательная

гиперболы-f — ^ = 1 и параболы y * = 2px (5） Смотрите каждый Р—гр =1.Вы= П * + Где (x&yo) — контакт. н°2.Общие линии метода являются своего рода перпендикуляром к кривой. Точное определение этого понятия таково: Нормаль кривой K в точке 1L — это перпендикуляр, который восстанавливается в точке M к касательной, проведенной

на Кривой K в той же точке M(см. рис.175). Угловой коэффициент касательной в точке M (x:* yQ) для кривой y = f (x) равен f (qi)= y%, помня условие перпендикулярности 2 линий, находим нормальное уравнение прямой (1) в точке M (d0, y o).）： Рисунок 175. XX, и если y ’ 0 = 0, то это уравнение не является available. In в этом случае

касательная параллельна оси Ox. So, так как Нормаль перпендикулярна оси Ox и проходит через[M(d0,y0)), то уравнение (6）Если записать (6) в виде V0 (V-V) = x0-x-с самого начала, то можно не различать эти случаи. Образцы. Нарисуйте нормали в точках I (=5) и B (x * = 2) к параболе y = 3x * −12 * + 8. Решение. Ордината точек A и B определяется из параболического уравнения и равна yA = 23,=

−4 соответственно. Кроме того, y ’= 6dr-12, где yr = 18 = 0.Таким образом, нормальное уравнение точки A Y-23 = −1(dg-5）、 И в точке Б х = 2.

Смотрите также:

Предмет высшая математика

Основные теоремы дифференциального исчисления	Направление вогнутости кривой
Формула Тейлора	Параметрическое задание кривой