Оглавление:

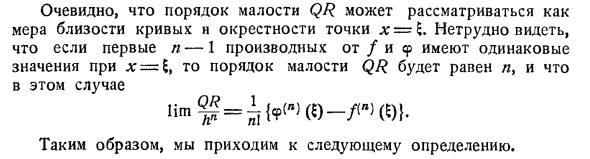
Касание плоских кривых
- Коснитесь плоской кривой. Если эта точка находится в каждой, две кривые призваны пересекаться в некоторой точке Из них. Если касательные совпадают в этой точке, это называется контактом в этой точке.
Предположим, что f (x) и 9 (π) имеют производные всех порядков m = £ и рассмотрим кривые y = f (), y = 9 (). В общем случае / ($) и 9 (£) не равны. В этом случае абсцисса x = i не соответствует пересечению этих кривых. Если f (t) = 9 (t), кривые пересекаются в точке jj =: f (t) = φ (t).
| Теоремы о среднем высших порядков | Касание n-го порядка |
| Ряд Тейлора | Действительные переменные |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- На этом этапе необходимо и достаточно, чтобы первые производные f ′ (*) и 9 ′ (π) имели одинаковое значение для = S, чтобы кривые касались друг друга. Кривая контакта в этом случае может рассматриваться с другой точки зрения. Рисунок 1 Нижняя кривая нарисована в контакте друг с другом в точке P. QR-сегмент 9 <8+ *) — / Нет. + «• И так как 9 10 = / («), 9 (5) = / (6),
Равно 4 A3 {NR «(SН-ОЛ) — /» + ОЛ)}, потому что 0 находится в диапазоне от 0 до 1, Iim 1? = 4 как h • — * 0. То есть, если кривые касаются друг друга в точках абсциссы, разница между ординатами в точке, где абсцисса составляет 5 мкл, по меньшей мере на два порядка меньше по отношению к h. О я 7 Фаг 42 Очевидно, что небольшой QR-порядок можно рассматривать как меру близости кривой и точки x.
В этом случае Iim (£) — / (a) (£)}. Поэтому определение таково. Людмила Фирмаль

