Оглавление:

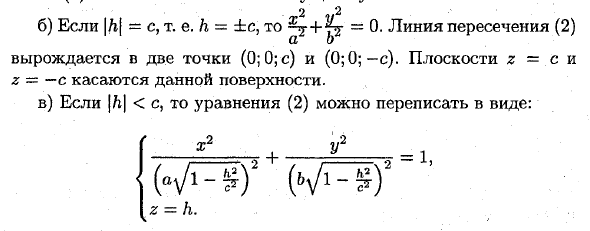

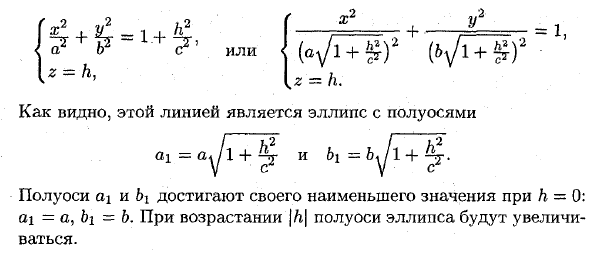




Канонические уравнения поверхностей второго порядка
- Каноническое уравнение поверхности второстепенный Определяет его геометрическую форму в соответствии с заданным уравнением квадратичной поверхности (т. Е. Поверхности, у которой уравнение декартовой системы координат является квадратичным алгебраическим уравнением). фДля этого мы применяем так называемый метод section.
1. эллипсоид Изучите поверхность, заданную уравнением x2 y2 z2 Рассмотрим сечение (1) поверхности с плоскостью, параллельной плоскости xOy. Уравнение для такой плоскости: z = A, где h — любое число. Линия, полученная в сечении, определяется двумя уравнениями x2. £ _ n h2 7 + V ~ 1 «(2) z = h. Изучите уравнение (2): 2 а) Если / / i |> c, c> 0, то + pr <0. Нет пересечения поверхности (1) и плоскости r = h.
Изучите внешний вид поверхности, изучив пересечение этой плоскости с координатной плоскостью или параллельной плоскостью. Людмила Фирмаль
2 2 б) если \ h \ = c, т.е. h = ± c, ^ r + pg ~ 0-пересечение (2) Уменьшите до двух точек (0; 0; c) и (0; 0; -c). Плоскости z-c и r = -c касаются указанной поверхности. c) Если | | i | <c, уравнение (2) можно переписать в виде + y! _ = 1 ». I-h 9 AJ 2G = ч. Как видите, линия пересечения представляет собой полуосевой эллипс , 2 * Кроме того, чем меньше | j |, тем больше полуоси a1 и b1. Если h = 0, максимальное значение достигнуто: a \ -a, = b. равных С * 2 + 4 = 1 (2) принимает форму <a b [/ i = 0. Рассмотрение сечения поверхности (1) с плоскостями x = h и y = 1r дает аналогичные результаты.
Таким образом, в зависимости от рассматриваемого сечения поверхность (1) может быть нарисована как замкнутая эллиптическая поверхность. Поверхность (1) называется эллипсоидом. Величины a, b и c называются полуосью эллипсоида. Если они все разные, то эллипсоид называется трехосным. Трехосный эллипсоид является сфероидом, если две полуоси равны. Если a = b = c-к сфере x2 4-y2 4-z2 = a2. 2. Гиперболоид Гиперболоид с одной полостью Изучите поверхность, заданную уравнением x2 v2 z2 Обход плоскости (3) с плоскостью 2 = h дает пересечение уравнений вида А б \ = т / 1-
| Цилиндрические поверхности | Понятие множества. Логические символы |
| Поверхности вращения, конические поверхности | Функция |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- fx2 h2 [* 2 i, y2 u = U = l. Как видите, эта линия представляет собой полуосевой эллипс b1 = + и 6, = 1 + Полуось ai достигает минимального значения при Л = 0. Qi = a, & i = 6. По мере увеличения полуось эллипса увеличивается.Если вы пересекаете грань (3) с плоскостью x = h или y = A, вы получите гиперболу в поперечном сечении. Например, найдите пересечение поверхности (3), которая является уравнением (x = 0), и плоскости Ойза. Эта линия пересечения является уравнением Как видите, эта линия — гипербола. Анализ этих разделов показывает, что поверхность, определяемая уравнением (3), имеет бесконечно расширяющуюся форму трубки.
Примечание. Вы можете доказать, что в любой точке (3) на гиперболоиде есть две линии. 2 гиперболоида Поверхность задается уравнением 2-, 2 2 Jr + Jr-FR — 1-. (4) Если поверхность (4) пересекает плоскость r = h, линия пересечения определяется уравнением (X2 l Y1 h2 {? + P ~ 7 «lj (5) (Z- / г. Это так. а) Если если | / i | <c, плоскость z-h не пересекает поверхность. б) При \ h \ = c плоскость r = ± c касается этой поверхности в точках (0; 0; c) и (0; 0; -c) соответственно.
Поверхность (3) называется одним гиперболоидом. Людмила Фирмаль
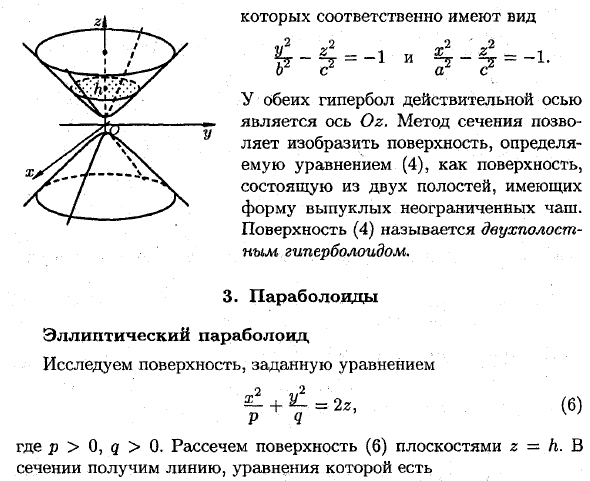
c) Для \ h > c уравнение (5) можно переписать в виде:f + f8 i 1 Эти уравнения определяют эллипс, полуось которого равна [A | Пересечение поверхности (4) с координатными плоскостями Oyz (x = 0) и Oagg (y = 0) приводит к уравнению в гиперболическом сечении.У каждого есть форма .2 2 x2 б Z _ 1 — t — 1 и -g _ 1 ? В обеих гиперболах действительной осью является ось O-g.
Используя метод поперечного сечения, поверхность, определенная уравнением (4), может быть нарисована как поверхность, состоящая из двух полостей с бесконечной выпуклой формой чаши. Поверхность (4) называется двухрезонаторным гиперболоидом. 3. Параболоид Эллиптический параболоид Изучите поверхность, заданную уравнением -4- = 2z, P I Где p> 0, q> 0. Разрезать поверхность (б) в плоскости сечения d и уравнение (6) ч. в
П я z = h. Если h <0, плоскость поверхности z = h не пересекается, если Λ = 0, плоскость z = 0 касается поверхности в точке (0; 0; 0), а если h> 0, сечение Имеет эллипс уравнений + J / 1 = 1 2pK + 2qh ‘ .g = ч Его полуось увеличивается с увеличением h. При пересечении поверхности (6) в координатной плоскости g2 y2 Oxz и Oyz получают parabola.r = u и 2 = u соответственно. Следовательно, поверхность, определяемая уравнением (b), имеет форму выпуклой бесконечной чаши. Поверхность (6) называется эллиптическим параболоидом.
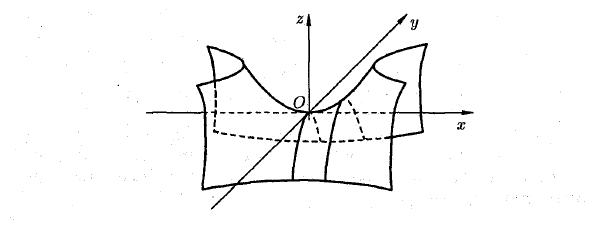
Гиперболическая парабола Изучите поверхность, определяемую уравнением X2 U2 —— = (7) П я Где p> 0, q> 0. Разрезать плоскость (7) с плоскостью z = h. Вы получаете кривую 2 ph 2 qh ‘z = h Это гипербола для всех значений h ^ 0. Если h> 0, то Действительная ось параллельна оси Ox. если h <0, они параллельны 2? У2 Ось Оу; / i = 0, пересекают линию- = 0
Пересекающиеся пары линий — = 0 и -f Jjj = 0 у ~ к Ветвь вверх. Оказывается, если у = 0 в разделе (X2 = 2T) Z Имеет вершину в начале координат и ось симметрии Y = 0 Toriaozu Если плоскость (7) пересекает плоскость x = f, то ветвь параболы y2 = — вращается вниз. Анализируя линию пересечения, можно определить тип поверхности. Это в форме седла. Поверхность (7) называется гиперболическим параболоидом.

