Оглавление:






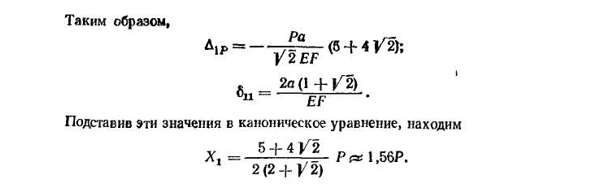

Канонические уравнения метода сил
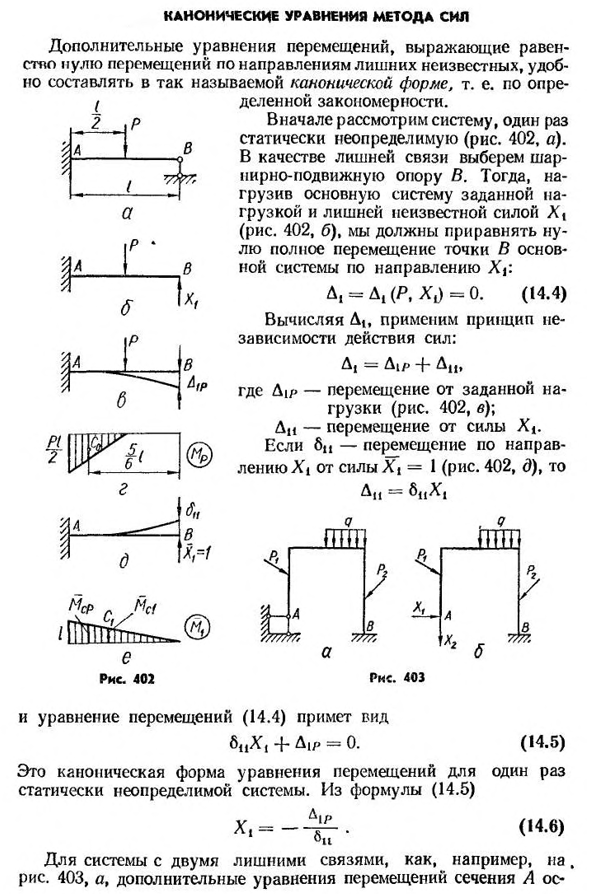
- Канонические уравнения силового метода Дополнительное уравнение смещения, представляющее собой равное нулю смещение в направлении дополнительного неизвестного, имеет так называемую каноническую форму, то есть,、 Рис четыреста два Разделенная регулярность. Сначала рассмотрим некогда статически неопределенную систему(рис. 402, а). Тогда нагрузка нагрузка дается в основной системы и лишних неизвестных х(рис. 402, б), мы должны приравнять ноль к общему движению точек в основной системе в направлении X f D1=(P, X J=0. (14.4) Вычислите применимый принцип независимости силы: D|=Air+AI, где D1 / > — движется
от заданной нагрузки(рис. 402, в) \ DC-смещение от силы Х4. Если 6I-движется в направлении Xi Сила 1=1(фиг. 402, б)、 AI=^11^1 Рис четыреста три И уравнение перемещения (14.4) принимает вид 6cx (+A1/>=0). (I. 5) это каноническая форма уравнения перемещения для некогда статически неопределенной системы. Из Формулы(14.5) х(14.6) °11 Для систем с двумя дополнительными соединениями, например, h a, фиг. 403, а, дополнительные уравнения перемещения секции ОС а- Фоновая система(рис. 403, Б) принимает вид В=0; Л2-0″ — D1 (P, XH X2)-неизвестная мощность, необходимая при заданной нагрузке x ltx2, да-направление X I точки полного
движения от DG (P, Xt, x2) — направление X2 точки от заданной нагрузки Исходя Людмила Фирмаль
из принципа независимости действия сил, можно сделать вывод, что движение D (а D2-сумма перемещений, вызванных отдельно каждой неизвестной силой x x2 и заданной нагрузкой R). D: = DC+D12+Aip=0;(14D2-D21F D22+DGR=0. Полное перемещение D m OJ можно записать как произведение некоторого перемещения b, K, которое вызвано действием единичной силы, и величины соответствующей обобщенной силы: DC-btshr D|2=** * >Alft=^X K. Таким образом, уравнение (14.7) принимает вид BCC|4-b/2X2″B L1R»0*62tXt-|-822X2X2DP-0. (14.8) Это каноническая форма уравнения смещения для системы, дважды статически неопределенной. По аналогии можно записать уравнение перемещения произвольной n-кратной статической неопределенной системы в каноническом виде: W+ ^12^2 + • • • + B1ph p f L / R— 0; + ^22^2 + • • • + ^GPH » f D2p=0; (14.9) f6p2×2f• * * 6″ » хй ф д|р-0. Перемещения, входящие в ДГР и канонические
уравнения, чаще всего определяются методами Мора или Верещагина. При этом в случае балок и шпангоутов влияние поперечных и продольных сил обычно игнорируется, учитываются только изгибающие моменты. Однако для того, чтобы определить перемещение балки прямоугольного сечения, необходимо учитывать отношение высоты поперечного сечения к поперечной длине пролета y->p. при расчете статически неопределимой рамы с большим значением указанного отношения!- t — >продольные и поперечные силы также становятся значительными, ошибка, вызванная пренебрежением интегралом 401specially для высокой рамки. Заметим, что в конструкции реальных балок, рам и арок соотношение — ■обычно меньше, чем-jy. Поэтому при определении смещения по общей формуле Мора вполне допустимо сохранение
- интеграла с учетом только изгибающего момента. Чтобы определить смещение, постройте график изгибающего момента(например, фиг. 402)в основной системе задается нагрузка(состояние Р) и каждая единица силы отдельно: Xi=1(Состояние 1); x2—1(состояние 2);…; X p-1 (p-состояние). Вертикальная ось соответствующего графика показана, как обычно, Mr, Mi, Mg… М, п. Затем, исходя из Формулы (13.46)、 С «•••»&ПИАР — с Некоторое смещение, имеющее тот же индекс и называемое главным коэффициентом канонического уравнения, определяется как: С Очевидно, что эти шаги позитивны. Определенное смещение с неравным показателем и называемым боковым коэффициентом определяется по формуле С С Они могут быть положительными или отрицательными, а могут быть и нулевыми. Основанный на теореме взаимности смещения В
системе, состоящей из прямых элементов, удобно рассчитать смещение по методу Верещагина. Например, Статический неопределенный луч показан на рисунке. Четыреста два, Но рмср^Р=—^ — ;СЗК=~Л Противоречие 402, л » ПП. К Р а’р——— 48£J ’ ° » ~i f T * Из Формулы (14.6) x, — 4-р. В таких случаях, когда, помимо внешних нагрузок, необходимо учитывать влияние температуры, процедура расчета остается прежней. Свободный член канонического уравнения представляет собой перемещение в основной системе не только от заданной нагрузки, но и от изменения температуры: + ^12^2 + • • * + M p+AiP+D1G=……………………………………………………………………………… (14.10)) 6«] X1 4 «6/yx2+ * ’* 4 » ^X * 4 — & PR+ & PT= = 0, Где D / g-смещение основной системы в направлении силы x t, вызванное изменением температуры.
С определенными коэффициентами 6^и свободными членами DGR и D^g, из системы линейных уравнений Людмила Фирмаль
(14.10) находим дополнительное неизвестное значение усилия X, если x2,…XL. затем обычным способом строим график элементов системы с внутренними силами/V, Q, M. иногда удобно построить график путем сложения графика M R plot M i9L42, M P9 с предварительно умноженным значением X it y y. ^2″* * p* Л1=MjXi+м2^2 + ••• + м-р; м=QiXj+QzX2+ * • * +qpj успешно Н=Н jXj-Джей/V2X2 4″••* — [Н П. Важно отметить, что в возможных вариантах базовой системы буквенная форма нормального уравнения не изменяется. Меняется только геометрический смысл ненужных неизвестных и перемещений. Например, если выбрать в качестве ненужных неизвестные внутренние силы в любом сечении, то коэффициенты канонического уравнения будут равны соответствующей силе сечения в направлении ненужной неизвестной силы. Для риса. 404 показаны три градуса постоянной плоской рамы (а) и два варианта основной системы
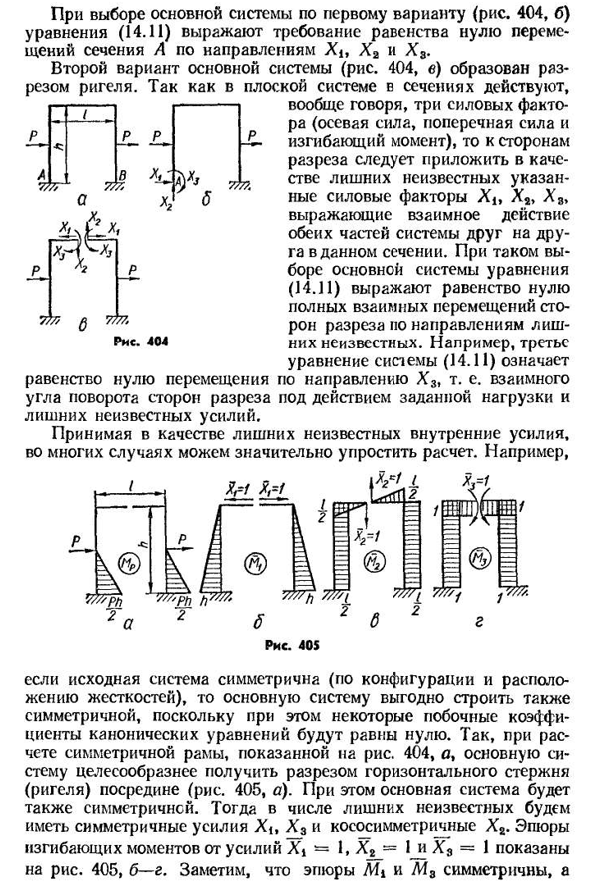
(6 и Б). Для любой трехградусной статической неопределенной системы нормальное уравнение принимает вид 8cx1+6(2×2)-$13×3 4D / R=0; B2 (Xf4-622X2 4-623X3 4-D2P=0;631^14″632×2 4″633×3 4-DZR=0. (14.11) 403 путем выбора основной системы согласно первому варианту(фиг. 404, б) уравнение (14.11) выражает требование о том, что оно равно нулевому смещению сечения а в направлении х х 2 и Х 3. Второй вариант основной системы(рис. 404, в) образовано поперечным сечением поперечины. Вообще говоря, поскольку в плоской системе в разрезе имеются три силовых коэффициента (осевая сила, боковая сила и изгибающий момент), то на кромках разреза обозначается ненужная неизвестная сила, при выборе такой базовой системы уравнение(14.11) обнуляет общее взаимное
равенство сторон разреза в направлении дополнительного неизвестного числа перемещений. Например, третье уравнение системы (14.11) представляет собой взаимное вращение сторон разреза под действием нулевого движения в направлении X3, то есть заданной нагрузки и ненужной неизвестной силы. Принимая ненужные неизвестные внутренние усилия часто может значительно упростить расчеты. Например, Рис четыреста пять Когда начальная система симметрична(конфигурация и положение жесткости), основная система строит симметричную систему, потому что некоторые боковые коэффициенты канонического уравнения становятся равными нулю, что показано на рисунке при расчете
рамки симметрии. 404, а основную систему целесообразнее получить разрезом горизонтального стержня (перекладины) в центре(рис. 405, а). В этом случае основная система также будет симметричной. Затем, в дополнительных неизвестных, мы получаем симметричные силы xy X3 и кососимметричные x2. На рисунке показана фигура изгибающего момента от силы X4-1, x2=Ijh X3=1. 405, b-G. заметим, что графики Mi и M3 симметричны, и участок l4a является кососимметричным. Умножение симметричного графика на перекошенный симметричный график приводит к нулю. Определим смещение B12=B21. Используя метод Верещагина, вы можете использовать 8″ — e g(-4—t+ 4 — — 4 — ) = 0 — < N / 2 ) Точно так же 23, 32-0. Таким образом, система уравнений(14.11) упрощается и принимает вид +«Л4*=0; 4 «^2R=0;(14.13) » z L+A33X3+DZR=0. Если заданная нагрузка P косо симметрична(рис. 404, а), то график l4r
также косо симметричен(рис. 405, а) и переместить D1R = DZR= = 0. Тогда из первого и третьего уравнений (14.13) следует, что симметричная сила в точке разреза равна нулю: ХВ=0;Х3=0. Обратите внимание, что если нагрузка симметрична, то график Mr также симметричен и D2P=0. Тогда из второго уравнения (14.13) следует, что кососимметричная сила x2=0. Например 65. График коэффициента силы на элементах каркаса показан на рисунке. 406, а. рама нагружена равномерно распределенной нагрузкой q, приложенной к горизонтальной перекладине (перекладине). Легко видеть, что система не определена статически дважды. Для риса. 406,6—g указывает на несколько возможных вариантов эквивалентной системы. Для гонки- Рис четыреста шесть Давайте рассмотрим варианты, показанные на рисунке. 406,6. Чтобы определить две дополнительные неизвестные силы и XA, мы используем
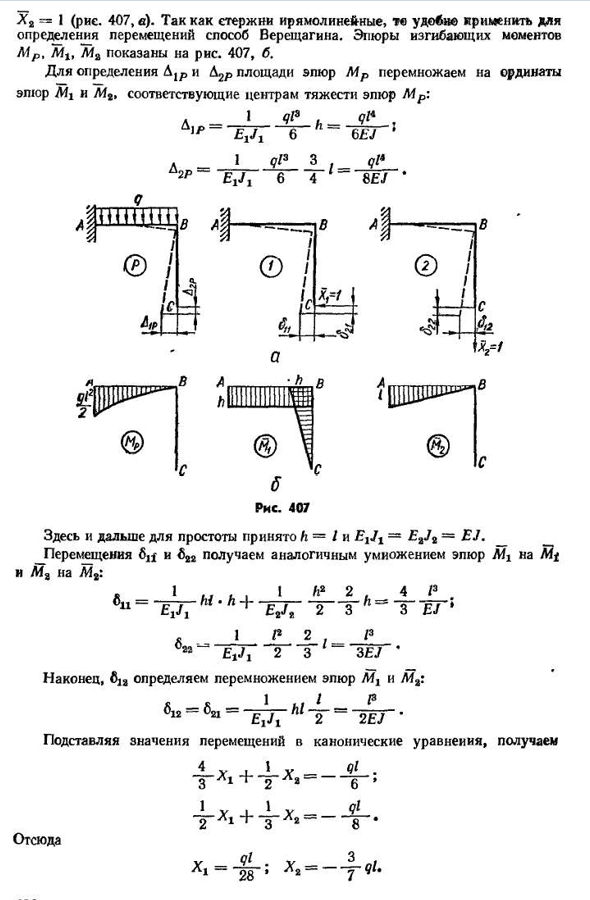
каноническое уравнение (14.8″:+612ha » B D / p=0;^2iXj+622X2+ — d / p) для определения смещения данной нагрузки отдельно., 405X2=1 (Рис. 407, в). Так как стержень прямой, то его удобно менять, чтобы определить движение по закону Верещагина. Фигура изгибающего момента АФА показана на рисунке. 407, б. Чтобы определить площадь D и D2p участка, умножьте центроид участка на соответствующий участок и вертикальную ось L / 2. Один. И H~I и E1J1=E2J2 = E j принимаются здесь и используются, чтобы сделать его еще проще. Смещения 6^и B22 получены умножением эпюры Afj на L42 M/n MA: < * 11= ’м’+ Один. ^2^2 И2 2(4/3 2 3 3£ / 1×1P2,/z22E iJi2 3 3 3 3EJ4 наконец, Dja определяется умножением графика Afj на Afa: R1s,
I P ~ 2 1~ » E G’g n T~ ~ 2 2E-величина смещения канонического И так оно и есть. Знак формулы 406X2 «минус» является первым выбранным направлением этой силы (рис. 406, Б) должно быть изменено на противоположное. Принимая во внимание эквивалентную систему под действием сил X^и X2, наблюдаемых при данной нагрузке, то есть базовую систему, статически определимую, рассматривается конечный процесс коэффициента внутренней силы. На рисунке показана конечная фигура изгибающего момента, боковых и осевых сил. 403. Выберите прямоугольное поперечное сечение стержня каркаса q= * I TC/m, I — = 2m, затем материал стержня ST2, (a]=1400kgf/cm2,[t]=900kgf / cm*. Отношение высоты поперечного сечения a к ширине B равно 2: 1. Как видно из диаграммы внутренних
усилий(рис. 408), в опасном поперечном сечении Чшкс= = 43-103К г с. с М.; QMaKc=X=1143кгс; Поскольку осевое усилие пренебрежимо мало, размеры сечения выбираются только из условий прочности на изгиб:= = MC.— 43 * 103 3 q3[a] −1400′ Как 6 ’12′ Затем, округляя, получаем 12 * 30. 6cm7. 2 см; b=~= = 3,6 см; W=31. 1cm3. Максимальное нормальное напряжение на площади поперечного сечения определяется как сумма напряжений от действия изгибающего момента и осевой силы: ^max,/V / 43 000 71,5,9, » max — — — — — — th/ — +T= \ — 3M-+7,2•3,6 кгс / см=<138°+H2 Максимальное касательное напряжение t max=4 ″ — Q f K — =2 3 7,243,6 кгс / см2=6 5, 5к г с / см<9 0 0К^ / ^с- Пример 66, вычислить однопролетную рамку (рис. 409 нагруженный с силой P горизонтальной в середине левой полки). Чтобы облегчить вычисление, предположим, что h=1; El J1=£2J2=E3J3=E J9 Система, которая представляет собой один замкнутый контур 407, является
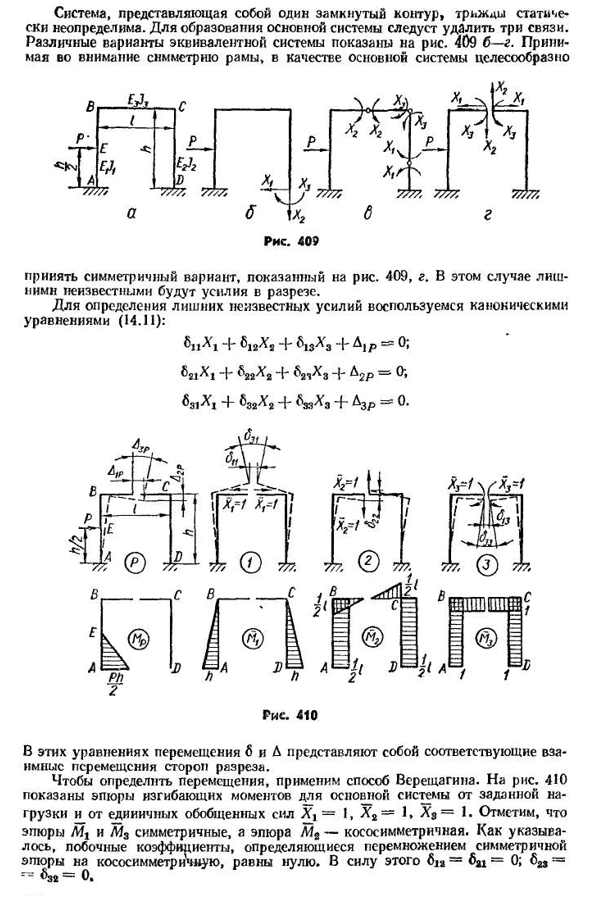
трижды статической неопределенной. Три ссылки должны быть удалены. Различные варианты системы эквивалентности показаны на рисунке. 409b-G. учитывая симметрию рамы, как основной системы, целесообразно Рис четыреста девять Как показано на рисунке, примите симметричную форму. 409, г. В этом случае лишние неизвестные будут усилия разделе. Для определения избыточной неизвестной силы используется каноническое уравнение (14.11): +^12^2+ » Б Л]Р== = О» ^21’^1 ″ Я «^22^2N ’ ^2 3^3+^2R Рие четыреста В этих уравнениях перемещения 6 и A представляют соответствующие взаимные перемещения стороны разреза. Для определения движения применяют метод Верещагина. Для риса. На рис. 410 показан график изгибающего момента основной системы от заданной нагрузки и единичных обобщенных сил Xj=1,
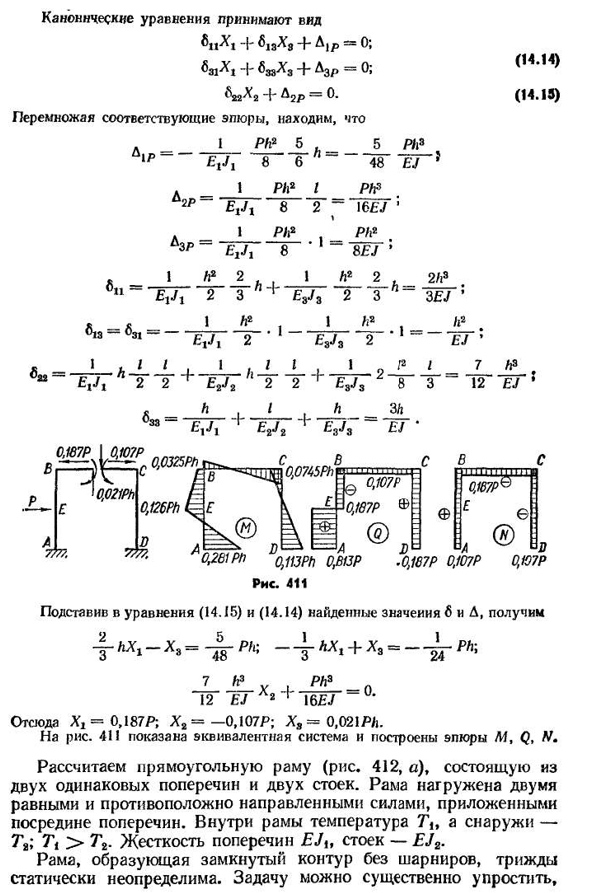
B B участки Mi и M3 симметричны, а коэффициент определяется умножением симметричного участка на косой симметричный участок в сторону нуля, как показано на рис.410. Для этого 61A=631=0;623= — B32=0. Уравнение канона 408 принимает вид +^13^3 + Ajp= » W L+^38^3+&WR= (14.14) ^22^2 + ^2P=0*(14.13) Если вы умножите соответствующий участок、 л __1Ph2 5. 5Ph3iP е т Дж Т8 6ч ~ таможня 48t Г’ Один Ph2PH1I>я Р Е в л Т2 8~И6£и J’ Один Я РН2, РН2 3Р-ЭГ С8 8EJ’ l1L2 2,, 1L2 2t2L3n «E1L2 3» * ’ £SJ3 2 3 3EJ ’L6, 3l1L2, L2 631-Et J t2′ £8J3 2’EJ ’ x_I u i, I, i,\P I7tp, 22Ev! x2 2+£2J2 2 2 2E3J3 2 8 3-12£J1x h1h ZL33 -£, -/, E2J2E3Ja-EJ • Рис четыреста одиннадцать Если присвоить выражения (14.15) и (14.14)найденным значениям 6 и D, то получится 4-M1-x, 4 — и C_4-LX,+X. — ^ — Нет. Семь. Двенадцать. ft3y Ph3EJ2«R16 на£Дж; Х I=0,1 8 7р; Х2=-0.107 П; хз=0,0 2 1П/Дж. Для риса. 411 показывает
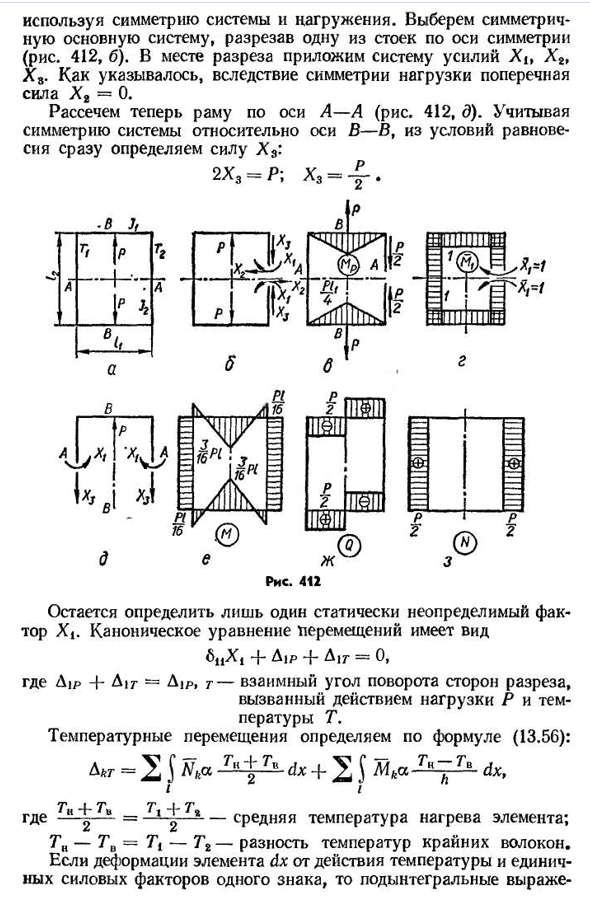
эквивалентную систему и строит графики L4, Q, V. Вычислите рамку прямоугольника(рис. 412, А) состоит из двух одинаковых поперечин и двух стоек. Рама нагружается двумя равными и противоположно направленными силами, приложенными к середине перекладины. Внутри рамы температура титана и снаружи T2; l>l-JIT полка в поперечине e-ej2 жесткость. Рама, образующая замкнутый контур без шарнира, трижды статически неопределима. Задачи могут быть значительно упрощены, 4W÷симметрия системы и нагрузки. Выберите базовую систему симметрии, разрезав одну из стоек вдоль оси симметрии(рис. 412, б). Примените систему сил x t, x2, X3 в месте разреза. Как показано, для симметрии нагрузки поперечная сила x2=0. Теперь разрезаем каркас по оси а-а(рис. 412, б). Учитывая симметрию системы относительно оси B-B, сразу определим силу X s из условий
равновесия: 2×3=P’, X3=4′ В п $ Л1 TlTrJ < URL-адрес п 1gptpivm Пятьдесят. 1.Один. ysh1l1n В W7 Один. Л. К. Остается определить только один статический неопределенный фактор XY-каноническое выражение перемещения, вид^CX{+Ai√4 «~O», где D1P4-воздух=D|p, g-нагрузка P и температура T=D / p. Температурное смещение определяется по формуле (13.56): D=2J Nka G,-(dx+2J m ka dx, — t — = — 1 — ^—C-экстремальная температура нагрева элемента. Tn-T=7\ — Tg-разность температур экстремального волокна. Если деформация элемента dx от действия температуры и единичных силовых коэффициентов одного знака, то подынтегральная функция Но результаты положительные. Если температура постоянна на графике, то=2{Nka I+a2k z2k / m dxj — =a^(здесь N k I+Qk-T-» — T°y) lk=pWftdx — площадь участка для определения смещения, P 412, e, a). Сюжет-ноль.
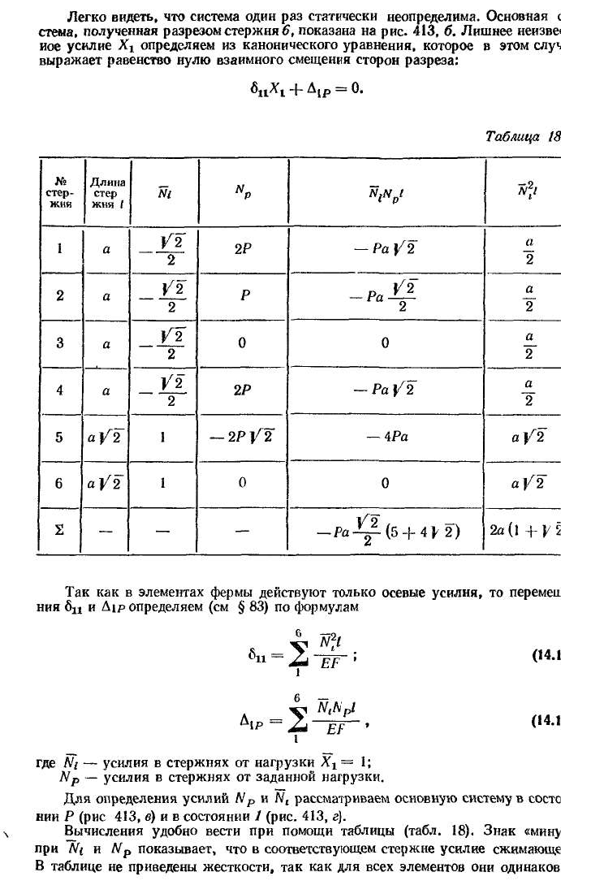
Используя метод Верещагина, мы выясняем Л—А — Ш » • ИЖ ° ~е Т8~4EJt • ч= — 2а(л+Л2). В правой части Зжс можно проверить знак» минус » и одинарный, чтобы под рамой 7>7а отечественные текстильные элементы стали длиннее(рис. 412, а) — сжатие. В дальнейшем, И так оно и есть., Для Lt=Z2-I Рис: сорок три Для риса. В случае 412\ — T2-дан график E-z коэффициента внутренней силы O, P=/=0. 67, например. Рассчитайте ферму, показанную на рисунке. 413, и в предположении, что все полюсы изготовлены из одного и того же материала и имеют одинаковое поперечное сечение, полюсы 5 и 6 не имеют общих узлов. Легко видеть, что система 411 не однажды определена статически. Основная ц Стея, полученная при разрезании стержня 6, показана на рисунке. 413, б. избыточная нелинейная сила X d определяется в этом случае из канонического уравнения,
представляющего собой равенство нулей взаимных перемещений сторон сечения: =0. Таблица 18 №. Стержень. Длина стержня 1 «Р Ж 2! Один. На П2 Два. 2Р — РА u2. А2 Два. Но 2/2 Два. Р -?■С Два.» Три. Но 1^2 Два. Ноль. Ноль. г 4а К2 Два. 2Р-Р а|^2а Тонны 5a^2 1-2R/2-4RA a/2 6A V2 V2 1 0 0a]«2 С — — — — П а — ^(5 — | — 4 F2) 2A(1+F2 Поскольку на элемент фермы действует только осевая сила, переменные DP и Aip определяются по формуле (см.§ 83). Шесть. =2 Один. EF9 (14.1 б Н^Пи эф’ (14.1 Один. Где Ni-сила в стержне от нагрузки X r=1, Np-сила в стержне от данной нагрузки. Для определения сил Np и Nt рассмотрим основные системы состояний P(рис. 413, Б) и состояние 1 (Рис. 413, г). х Удобно производить расчеты с помощью таблиц (вкладок). 18). Символы «mine» и A/p указывают на то, что соответствующая сила сжатия стержня в таблице одинакова для всех элементов, поэтому жесткость не задается 412 способами, Я d — = — tyg (5+4^,; 2O(1+^2) ФВ Подставляя эти значения в канонические уравнения, можно увидеть 5 + 4 / 2 2(2-hV2) P&1.56 p.
Смотрите также:
| Дифференциальное уравнение изогнутой оси | Влияние высоких температур на механические свойства металлов. |
| Расчет простых статически неопределимых балок | Явление ползучести и релаксации |

