Оглавление:




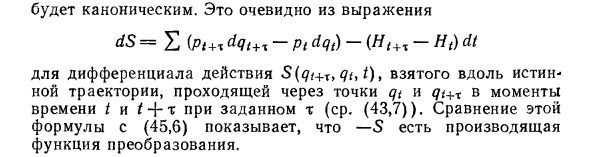

Канонические преобразования в физике
- Регулярное преобразование. Выбор обобщенной координаты q Условие — может использоваться любое однозначно определенное значение Делит положение системы в пространстве. Формат уравнения Лагранжа (2.6) не зависит от этого выбора, В некотором смысле уравнение Лагранжа инвариантно относительно преобразования из координат gi, q2, ….
Другие независимые величины Qi, C? 2> ••• Новая координата Q является функцией старой координаты q, и их выбор разрешен. Говоря о трансформации форм Qi = Qi (q, t) (45,1) (Их иногда называют точечными преобразованиями.) С лагранжевыми уравнениями для преобразования (45.1)
Однако последнее фактически допускает гораздо более широкий класс преобразований Людмила Фирмаль
Конечно, сохраните их форму (40.4) и уравнение Гамильтона. . Эта ситуация является гамильтоновым методом Отношение между p-импульсом и q регулирует роль независимой переменной равноправного узла.
Таким образом, вы можете расширить концепцию трансформации, чтобы включить трансформацию Новая переменная P из всех 25 независимых переменных p и q И Q по формуле Qi = Qi (P, q, t), Pi = Pi (p, q, t). (45,2) Такое расширение класса приемлемых преобразований является одним из основных преимуществ гамильтоновой методологии.
- Однако при любом преобразовании формы никогда (45.2) Уравнения движения сохраняют свою нормальную форму. Здесь мы выводим условия, которым должно удовлетворять преобразование, чтобы уравнения движения для новых переменных P и Q имели вид А ДН ‘• ДН’, л л = Нет ■ p <= ~ w, <45’3) Некоторые новые гамильтоновы функции Hf (P, Q).
В таких Конверсия является особенно важным так называемым стандартом. Формула регулярного преобразования может быть получена следующим образом. В конце § 43 было показано, что уравнение Гамильтона выводится из принципа минимального действия, выраженного в виде S J (52 пи дки-хдт) = 0 (45,4) (Кроме того, все координаты и импульс меняются независимо).
Однако их подынтегральные функции являются произвольными функциями Людмила Фирмаль
Чтобы новые переменные P и Q удовлетворяли уравнению Гамильтона, Принцип минимального действия 6 Дж [52 пи dQi-H’dt) = 0 (45,5) Однако два принципа (45.4) и (45.5) эквивалентны только друг другу. F k Ордината, импульс и время.
При изменении константы разница между двумя интегралами становится небольшой (разница в значении F в пределах интегрального предела). так так 52 Pi dqi-n dt = 52 Pi dQi-H’dt + dF Преобразование, которое соответствует этому требованию, называется стандартом х).
Все канонические преобразования характеризуются функцией P, называемой функцией преобразования генератора. Перепишите соотношение результата к форме dF = 52Pi dqi -5 2 Pi dQi + (I’-I) dt, (45,6) Мы видим это 3 F TU tt 1 tt I (LK * 7 \ «= P’ = -Щ’Я = Я + Ж; <45’7> Предполагается, что функция генератора задана как функция от старых и новых координат (и времени): F = F (q, Q, t).
Для заданной функции F выражение (45.7) устанавливает связь Он также дает выражение для новой гамильтоновой функции между старой (p, q) и новой (P, Q) переменными. Иногда полезно представить функцию генератора, используя старую координату q вместо переменных q и Q В этом случае для получения формулы канонического преобразования необходимо сгенерировать соотношение (45.6).
Соответствующее преобразование Лежандра. Другими словами, переписать его в следующем формате d (F + ‘iPi Qi) = Y, Pi dqi + ЈQi dPi + (#’ — H) dt. Представление под дифференциальным символом слева Уравнение, представленное переменными g и P, является функцией нового поколения.
Выражается как Φ (q, P, Ј), d) n = S ‘d = Нет.’ n = n + t (45’8> Точно так же мы можем перейти к формуле канонического преобразования, выраженной через производящие функции в зависимости от переменных p и Q или p и P. Обратите внимание на связь между новым гамильтонианом и старым гамильтонианом Функции всегда выражаются одинаково: разница Hr-H — частная производная по времени функции генератора.
В частности, если последний не зависит от времени, Hr = N. То есть в этом случае новый Функция Гамильтона — это величина p, q, Он представлен новыми переменными P и Q. Широта канонических преобразований лишает понятия обобщенных координат и их исходного импульса в гамильтоновом методе.
Преобразование (45.2) связывает величины P и Q с обоими координатами q и импульсом p, поэтому переменная Q больше не имеет смысла для чисто пространственных координат. разница Между обеими группами переменных в основном возникает проблема именования.
Эта ситуация очень четко показана, например, преобразованием Qi = Pi, Pi = —qi 2). Очевидно, что без изменения канонической формы уравнения это просто приводит к взаимному переименованию координат и импульса. Учитывая эту терминологию, переменные p и q Метод Милтона часто называют каноническим сопряженным.
Каноническое сопряженное условие По силе пуассоновской скобки. Для этого сначала докажем общую теорему об инвариантности скобок Пуассона для канонических преобразований. {fg} Пусть p и q — скобки Пуассона для / и g. Производная группы — это переменные p, q и {fg} p и Q — дифференцируемые скобки Пуассона одинакового количества С каноническими переменными P, Q {fg} p, q = {fg} p, Q • (45-9)
Эта связь может быть подтверждена напрямую Расчет с использованием обычной формулы преобразования. Однако вы можете опустить вычисления, используя следующие выводы: Во-первых, в канонической трансформации (45.7) или (45.8) время служит параметром.
Таким образом, Докажите теорему (45.9) для величин, которые не зависят явно Время, это верно для общего случая. Здесь мы рассматриваем величину g как гамильтониан чисто формальным образом. Некоторые фиктивные системные функции. Тогда, согласно уравнению (42.1), {fg} p, q = —df / dt.
Однако дифференциал df / dt представляет собой величину, которая зависит только от характеристик движения (фиктивная система), а не от выбора переменных. Следовательно, скобка Пуассона {/ g} Из обычных переменных Для других. Из уравнения (42.13) и теоремы (45.9) {QiQk} p, q = 0, {PiPk} p, q = 0, {PiQk} p, q = & ik- (45.10) Это условия, записанные с помощью скобок Пуассона, которым должны удовлетворять новые переменные, чтобы преобразования p, q-> P, Q были каноническими.
Изменения в p и q Движение можно рассматривать как каноническое преобразование. Смысл этого предложения заключается в следующем: Дай мне Значение стандартной переменной QtiPt-Time Ј, a qt + t, pt + t-значение в другой момент t + t. Некоторые функции бывшего Интервал t) в качестве параметра: Qt + r = q (qt, Pt, t, r), Pt + t = p (qt, pt, t, t)
Если мы рассмотрим эти выражения как преобразования из переменных qt и Pt в переменные qt + m и Pt + h, это преобразование является стандартным. Это ясно из формулы dS = Y, {pt + T dqt + m-Pt dqi) — (от Ht + m до Ht) dt Действие, предпринятое по истинной траектории, проходящей через точки qt и qt + h в заданные моменты времени t и t + m / 5 (<& + m, <&, Ј) производной (см. (43.7)) , Сравнение этого уравнения с (45.6) показывает, что -S является функцией преобразования генератора.
Смотрите также:
| Действие как функция координат в физике | Теорема Лиувилля в физике |
| Принцип Мопертюи в физике | Уравнение Гамильтона-Якоби |
Если вам потребуется помощь по физике вы всегда можете написать мне в whatsapp.

