Оглавление:
Задача №1.3.16.
Канат длиной 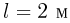 переброшен через блок. В начальный момент канат покоится и по обе стороны блока свешиваются равные его отрезки.
переброшен через блок. В начальный момент канат покоится и по обе стороны блока свешиваются равные его отрезки.
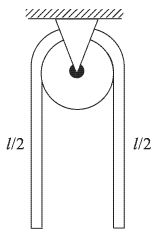
Затем, в результате незначительного толчка равновесие каната нарушается и он приходит в движение. Какова будет скорость каната V в тот момент, когда с одной стороны блока будет свешиваться отрезок каната длиной 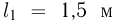 ? Массой блока и его размерами пренебречь, энергию толчка и трение в блоке не учитывать, ускорение свободного падения принять
? Массой блока и его размерами пренебречь, энергию толчка и трение в блоке не учитывать, ускорение свободного падения принять 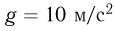 .
.
Решение:
Когда один из концов каната начнет перевешивать другой, канат придет в движение, причем его ускорение будет все время увеличиваться. В самом деле, поскольку по мере движения будет возрастать масса одной из свешивающихся частей каната и уменьшаться масса другой, будет соответственно увеличиваться сила, сообщающая канату ускорение. Поэтому попытка применить для решения задачи законы динамики обречена на неудачу, так как без привлечения высшей математики мы не сможем по переменному ускорению найти скорость тела. Но использование закона сохранения механической энергии позволит легко получить ответ.
Примем за уровень отсчета потенциальной энергии каната центр блока, обозначим через т массу каната. В начальном состоянии каната, изображенном на рисунке штриховой линией, по обе стороны от блока свешиваются одинаковые части каната длиной 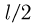 каждая (по условию задачи длиной отрезка каната, лежащего на блоке, можно пренебречь). Центры тяжести каждой из половин каната (обозначены на рисунке жирными точками) находятся на расстоянии
каждая (по условию задачи длиной отрезка каната, лежащего на блоке, можно пренебречь). Центры тяжести каждой из половин каната (обозначены на рисунке жирными точками) находятся на расстоянии 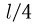 от уровня отсчета потенциальной энергии, масса каждой из половин равна
от уровня отсчета потенциальной энергии, масса каждой из половин равна 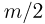 .
.
Следовательно, начальная потенциальная энергия каната равна:
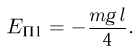
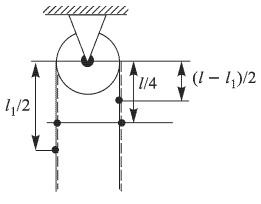
В конечном состоянии каната, изображенном на рисунке сплошными линиями, слева от блока свешивается отрезок каната длиной 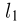 и массой
и массой 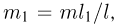 центр тяжести которого находится на расстоянии
центр тяжести которого находится на расстоянии 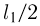 от уровня отсчета потенциальной энергии, справа от блока свешивается отрезок каната длиной
от уровня отсчета потенциальной энергии, справа от блока свешивается отрезок каната длиной 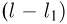 и массой
и массой 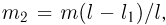 центр тяжести которого находится на расстоянии
центр тяжести которого находится на расстоянии 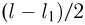 от уровня отсчета потенциальной энергии. В соответствии с этим, конечная потенциальная энергия каната равна:
от уровня отсчета потенциальной энергии. В соответствии с этим, конечная потенциальная энергия каната равна:
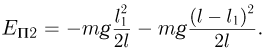
По закону сохранения механической энергии:
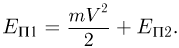
Объединяя записанные выражения, после несложных преобразований получаем ответ:
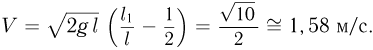
Эти задачи взяты со страницы решения задач по физической механике:
Решение задач по физической механике
Возможно эти задачи вам будут полезны:

