Калориметрическое определение энтропии химического соединения.

Калориметрическое определение энтропии химического соединения.

• Калориметрия энтропии КСИИМНЫХ соединений Рассмотрим 1 компонентную систему, которую мы хотим определить молярной энтропией калорически.Из основного уравнения(3.5） (9.3） Видно, что термодинамика позволяет вычислить не абсолютное значение энтропии, а только ее change.In для того чтобы приписать энтропии определенное значение, необходимо ввести условие, определяющее ноль энтропии.Условия определения нулевой энтропии различных веществ

Поэтому энтропию большинства кристаллических материалов можно считать равной нулю при абсолютной нулевой температуре. Есть исключения из этого общего правила, такие как CO (P. 197). В кристалле CO молекула может находиться в состоянии с несколькими различными ориентациями, даже при самой низкой температуре, достигнутой экспериментально.Энтропия стеклянных и аморфных твердых тел также не равна нулю при 0°К.

Однако гелий находится в жидком состоянии при этой температуре и давлении 1 атм, а энтропия гелия при 0 ° к равна нулю. Тот факт, что энтропия большинства веществ может быть установлена на ноль при 0°к, считается содержанием Нернста theorem.It не используется, но мы будем углубляться дальше в этот вопрос.

Однако как бы ни формулировалась теорема Нернста, необходимо помнить, что пределы ее применимости должны быть исследованы в методе статистической механики 3. Людмила Фирмаль

Интеграл от абсолютного нуля до температуры t(9.3)、 (9.4） Поскольку абсолютный ноль не может быть достигнут, этот Интеграл фактически является т. С / 1С) [Дж /) ‘ С интегральным пределом| 1-.. как T * — > 0 т. * Если предположить, что теорема Нернста применима к рассматриваемому соединению、 С(0)= 0 (9.5） И затем (9.6） 5 = $ Поскольку S является функцией состояния, путь, по которому выполняется интеграция, не имеет значения.Однако в общем случае при температуре T вещество находится в ином физическом состоянии, чем 0°K, поэтому путь интегрирования может содержать более 1 фазового перехода.Метод интеграции описан ниже.

В качестве примера выбирают вещества, которые являются жидкими при температуре T и давлении p. температура плавления вещества при заданном давлении равна Tf. Если температура 1 моля рассматриваемого вещества повышается при постоянном давлении от 0 до Tf, то система является однородной и однофазной, поэтому d (/будет равен нулю (см. главу III,§4), А D / будет равен нулю. гр гр. c’aq + dQ ‘ с использованием cPdT = $ — РГ. (9.7）

Где cmp-молярная теплоемкость твердого тела при постоянном давлении.Вещество плавится при температуре Tf.At при этом температура и давление Р, твердой и жидкой фаз находятся в равновесии, поскольку A = 0, d (/=0). в то же время Когда вещество расплавляется на 1 моль, оно становится= 1, а теплота поглощения равна молярной теплоте плавления а / / г вещества.Соответствующий вклад в энтропию Д / 7г / Т /. (9.8） Между Tf и T мы снова рассматриваем однородную 1-компонентную систему, и изменение энтропии при нагревании от T /до T равно Т. 5-т■ » и*. (9-9)） Т. Ф Где cp-молярная теплоемкость жидкости.

• Таким образом, энтропия жидкости будет: т. *(9.10） Tf. Аналогично, если вещество при заданной температуре и давлении является газом, то необходимо учитывать энтропию испарения Где cmp-молярная теплоемкость твердого тела при постоянном давлении.Вещество плавится при температуре Tf.At при этом температура и давление Р, твердой и жидкой фаз находятся в равновесии, поскольку A = 0, d (/=0). в то же время Когда вещество расплавляется на 1 моль, оно становится= 1, а теплота поглощения равна молярной теплоте плавления а / / г вещества.

Соответствующий вклад в энтропию Д / 7г / Т /. (9.8） Между Tf и T мы снова рассматриваем однородную 1-компонентную систему, и изменение энтропии при нагревании от T /до T равно Т. 5-т■ » и. (9-9)） Т. Ф Где cp-молярная теплоемкость жидкости. Таким образом, энтропия жидкости будет: т. **(9.10） Tf. Аналогично, если вещество при заданной температуре и давлении является газом, то необходимо учитывать энтропию испарения

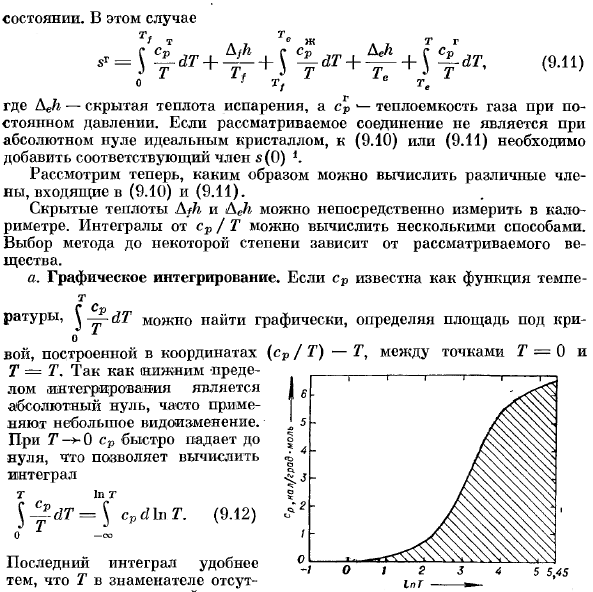
Л Х / Т. <р л Здесь Аджи-это скрытая теплота испарения, а также теплоемкость газа при постоянном давлении.Если рассматриваемое соединение не является идеальным Кристаллом с абсолютным нулем, то соответствующий член s (0)следует добавить к (9.10) или (9.11 Теперь рассмотрим, как вычислить различные термины (9.10) и (9.11). Скрытая теплота WC и Аджи может быть измерена непосредственно с помощью калориметра. Интеграл cp / T может быть рассчитан несколькими способами.Выбор того или иного метода зависит от рассматриваемого вещества. A. графическая интеграция. если cp известен как функция tempe-t С водой Соотношение,^ dT можно найти на графике, определить площадь ниже Вой построен по координатам (cp / T) — T между точками T = 0 и T-T. нижняя граница

Интеграла равна / 6 абсолютной zero.In во многих случаях используются незначительные изменения. При T 0 cp сразу падает до нуля, что позволяет вычислить Интеграл t в t. 5 5.45 Государства.В этом случае (9.11） №.ДТ= с (9.12）0.434 t 2J2 7.39 20.1 54.6 / 48.4 234 есть 7 *и- Отношения Т точнее.Графическое определение энтропии в качестве примера Применение этого метода к твердой ртути、

Последний Интеграл более удобен тем, что T не находится в знаменателе. Это верно;это делает графический. Людмила Фирмаль

На рисунке показана зависимость cp в твердой ртути 2 от hi T. A. численный метод.Если молярную теплоемкость cp можно определить как ряд возрастаний мощности T, то Интеграл легко вычисляется.Например、 СР = а + вт + ст * — К. И затем… Б(Т-т0)+±с(Т * — Т °、 СР =(а-F — БТ) СР°Ф Где A и B-константы, а cf° — теплоемкость алифатических соединений, выбранных в качестве стандарта качества. Таким образом, энтропию Бутана можно найти путем суммирования следующих величин (кал / град моль). 7.78 + 0.7 20.44±0.2: 1.95 0.14 0°~(57°K, экстраполяция 67°-131.1 ° K, кристаллическая графическая интеграция Плавления 1044.3 / 134.1 134.1°-272.5°к, жидкость Испарение 5324 / 272.5 272.5°-298.1°К (среднее<^ = 21.6） Неидеальная компенсация Общая энтропия идеального газа при 1 атм и 298,1°к 74, G9±1 (1 ^ Кил / ГПД моль. Вешалка. 8.

Смотрите также:

Предмет термодинамика

Разложение гексана.	Приближенные расчеты, основанные на теореме Нернста
Тепловая теорема нернста. Постановка задачи.	Идеальные газы. Уравнение состояния идеального газа.