Оглавление:






Как применять экономико-математические методы на практике
- Как применить экономику Актуальный математический метод Иметь дело с конкретной практической экономикой Задачи можно рекомендовать в следующем порядке: 1. Разъяснить проблему — ее экономические последствия. здесь Мы ставим цель для решения. 2. Оценить экономическую ситуацию. Положитесь на достижение поставленных целей. 3.
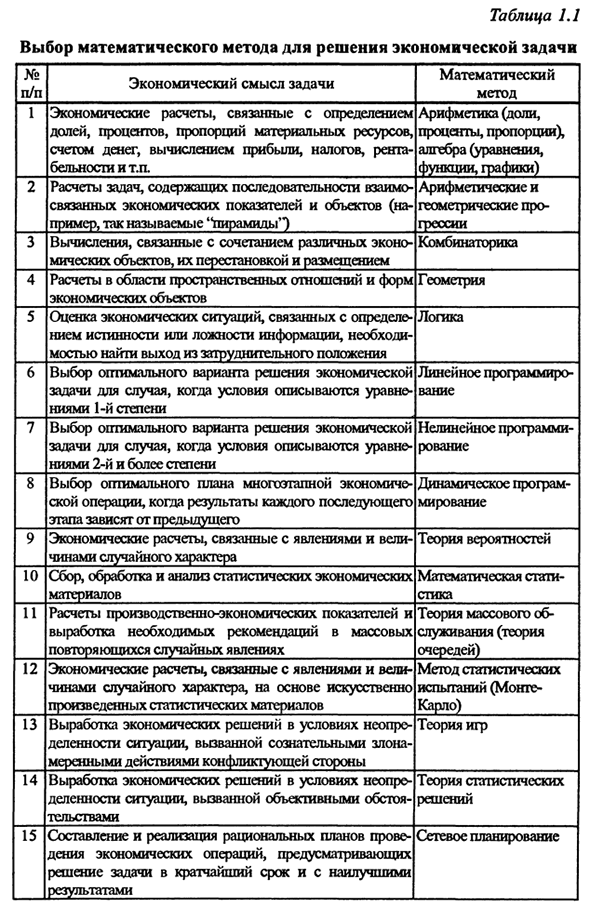
- Выберите числовой индикатор Достижение целей отличается в первую очередь. 4. Создать математическую модель работы. Установить количественную зависимость выбранных показателей Условие задачи. Смотрите таблицу для этого. 1.1 выберите Подходящие экономико-математические методы. 5. Обнаружено с использованием математических моделей.
Решать задачи методами экономической математики. Людмила Фирмаль
6. Проверьте правильность найденного решения. Лучшие практические соображения Экономико-математические методы на конкретных примерах. в В качестве первого примера этого возьмем пример 1 из введения. Итак по порядку: 1. Экономический смысл проблемы Похудения из-за высыхания у нас нет Прямые данные о потере веса продукта.
Целью решения является Косвенно определить, насколько вес был уменьшен из-за усадки Данные о сокращении продукта Жидкость. 2. Потеря веса зависит от изменения количества Жидкость, которая испаряется во время процесса сушки Уменьшите пропорцию продуктов. 3. Основными показателями похудения являются Абсолютное изменение, а не процентное изменение Жидкость.
Об изменениях удельного содержания жидкости Процент не означает, что вес продукта изменится на столько же Соотношение. 4. Математические модели должны устанавливать зависимости Абсолютное изменение веса продукта при усадке из-за изменения Процент воды. Наша задача — определить Проценты и пропорции как экономическая математика В методе рекомендуется выбирать арифметику и алгебру (см. Таблицу 1.1).
Выбор математических методов для решения экономических задач P / P 1 2 3 4 5 6 7 8 9 10 11 12 13 14 115 Экономический смысл задачи Экономические расчеты, связанные с решением Запас, процент, соотношение материальных ресурсов, Денежный счет, расчет прибыли, налог, Рентабельность и т. Д. Расчет заданий с последовательностями.
Взаимосвязанные экономические показатели и объекты (Например, так называемая «пирамида») Расчеты, связанные с различными комбинациями Хозяйственные объекты, их перестановка и размещение Расчеты в области пространственных отношений и форм Хозяйственный объект Из экономических условий, связанных с Судите правду или ложь информации, Нужно найти выход Выбор лучшего решения для экономики.
Задача, когда условие описано Линейное уравнение Выбор лучшего решения для экономики Задача, когда условие описано Квадратное уравнение Выбор лучшего многоступенчатого плана Каждый последующий результат Предыдущий этап Экономические расчеты, связанные с этим явлением и Случайная величина Сбор, обработка и анализ статистической экономики материал.
Расчет производственно-экономических показателей Создайте необходимые рекомендации вместе Регулярные случайные события Экономические расчеты, связанные с этим явлением и Искусственная случайная величина Статистические данные созданы Разработка экономических решений в условиях Неопределенность из-за сознания.
Вредоносное поведение сторон в споре Разработка экономических решений в условиях Неопределенность ситуации обусловлена объективными факторами ситуация Сформулировать и реализовать рациональный план Осуществление хозяйственной деятельности Решите проблему как можно скорее результат математика способ Арифметика (акции, Проценты, проценты) Алгебра (уравнение, Функция, графика) Арифметика и геометрический Advance.
Комбинаторика Геометрия 1 Логика 1 линейный программирование Нелинейное программирование тор динамический программирование Теория вероятностей Математическая статья-1 Палка 1 Массовая теория об-1 Сервис (Теория Выброс) Статистический метод 1 Тест (Монте Карло) Теория игр 1 Теория (лшистические 1 Из решения.
- Планирование сети Согласно алгебраическим правилам, Желаемый вес продукта при измерении второго содержания от χ Создать текучие и четкие уравнения. Математическая модель задачи: = 96% =. () 100 Вт Где 1 тонна — масса сухого остатка неиспаренной части Один и тот же продукт в первом и втором измерениях. Этот вес Определяется по результатам первого измерения содержания жидкости: 99% от 100 т до 100 т = 1 т 5.
Решение уравнения () дает: х = 100А = 25 т 4 6. Проверьте правильность решения. измерение 1 день второй Сухой остаток % 1 4 Вес, т 1 1 жидкость % 99 96 Вес, т 99 24 общая сумма % 100 100 Вес, т 100 25 Надо было доказать. В рассматриваемом примере, как и во многих других случаях Практические экономические вопросы, не нужно производить Оптимизация.
Вам просто нужно правильно рассчитать, что вам нужно Индикатор — получи единственно возможное решение. Людмила Фирмаль
В следующем примере требуется оптимизация. Это Введение часть примера 2. Перейдем к процедуре расчета. 1. Экономический смысл задачи — найти подделку Алмаз с минимальными затратами на взвешивание. Поэтому цель Решение: определение минимального времени взвешивания, Достаточно, чтобы обнаружить подделку. 2.
Количество измерений связано с обеими величинами Исследуйте алмазы и в порядке разделения на части Альтернативное взвешивание. 3. Потому что мы берем на себя вес чашки, Взвешивание должно быть сделано путем размещения различных количеств Камень по шкале.
Когда есть равное количество камня Обе чашки не сбалансированы, так что подделка Один из камней исключен из взвешивания. если Поскольку нагрузка на одну чашку легче, чем на другую чашку, Есть поддельные камни. Самый простой способ поиска — положить в одну чашку Положите несколько камней, а остальные на другой 26 бриллиантов. Это требует максимально возможного числа. Взвешивание -26.
Однако нас не интересует максимальное значение, но мы заинтересованы в минимальном значении. так Такой бюст (называется непрерывным при изучении работы Или «слепой») явно нам не подходит. Вы должны искать путь Приводит к менее рациональным вариантам Взвешивание.
Поэтому достижение цели Выбор разделения таких камней при взвешивании Количество взвешиваний сведено к минимуму. Основные показатели, от которых зависят результаты Целью является минимальное количество взвешиваний Приводит к решению проблем-поддельные определения Минимальная стоимость 4.
Математическая модель проблемы должна быть актуальной Минимальное количество взвешиваний и общее количество камней Количество камней в каждой группе при разделении. Аналогичная модель может быть построена с использованием одного Метод оптимизации линейного программирования (см. §1) глава 3) Установить правила направления, т.е. Разумное перечисление вариантов.
Для этой проблемы суть перечисления направлений: Разделите камень на три одинаковые части и разберите их Можно определить с помощью одного взвешивания на весах Какая из трех частей является стразами. тогда Часть, где обнаруживается подделка, снова делится на три части. До трех последних взвешиваются. Там нет трех камней.
Взвешивание стало понятно Указывает, какой камень подделка. Такое направление дробления Значительно уменьшите количество необходимых взвешиваний. здесь В примере нужны только 3. Посмотрите на язык математики: необходимый минимум Количество взвешиваний (Vмин) составляет Очевидное соотношение:
ВШИ 1 раз N = 3 ^ 3 = 3B-, откуда * Vn = 3, () Где N — количество исследуемых объектов. Это математическая модель проблемы. 5. Выполните численные расчеты. Подставляя в формулу () N = 27, N / 27 = 3 Вы можете видеть, что минимальная сумма необходима Взвешивание 3. 6.
Расчет можно легко проверить, выполнив мысленный эксперимент. Первое взвешивание. На шкале 9 камней. Определите, какие 9 являются поддельными. Второе взвешивание. На шкале три камня. Определить тройную подделку. Третье взвешивание. Один камень на каждую шкалу. Я нашел фальшивый бриллиант. Надо было доказать.
Смотрите также:
| Какие бывают экономические методы и что они могут | Дроби, доли, пропорции и основные действия арифметики и алгебры |
| Что означают слова «правильное», «оптимальное» решение | Простые и сложные проценты |

