К середине троса подвешен груз массой

Пример решения задачи №71.

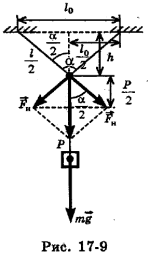
К середине троса подвешен груз массой m = 50 кг (рис. 17-9). Угол, образованный половинками троса, 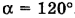. Найти силу натяжения 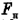каждой половинки троса. Чему равно удлинение троса 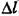, если в нерастянутом состоянии его длина м? Чему равно провисание троса h?

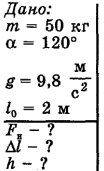
Решение:

К грузу приложена сила тяжести 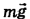, а к тросу — вес груза 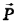. Поскольку все тела покоятся, вес груза равен силе тяжести:

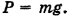
С другой стороны, вес груза 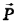есть векторная сумма двух сил натяжения половинок троса, поэтому вес является диагональю ромба, сторонами которого служат силы натяжения.

Поскольку угол а между векторами равен углу между половинками троса как вертикальные углы, угол между векторами равен .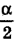

Треугольник, в котором вектор 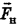является гипотенузой, а половинка веса 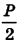— катетом, прямоугольный с углом 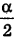, прилежащим к катету 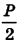, поэтому 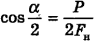, откуда 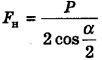или

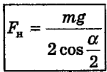
Изменение длины троса 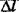равно разности длин l в растянутом и 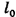в нерастянутом состояниях: .

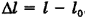В линейном прямоугольном треугольнике с гипотенузой 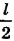и катетами 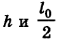угол, прилежащий к катету h, тоже равен 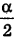, поэтому 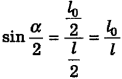, откуда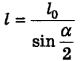

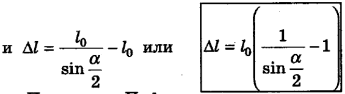
По теореме Пифагора

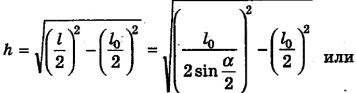
Произведем вычисления:

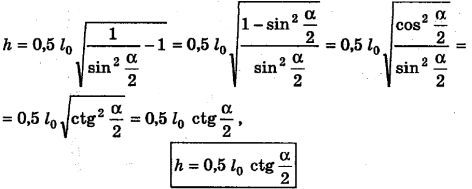
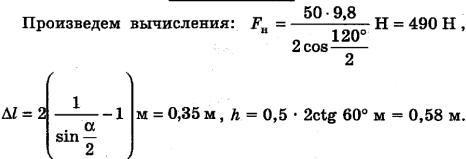
Примечание. Для уменьшения количества индексов здесь и далее одинаковые по модулю векторы сил натяжения мы обозначаем одинаково.

Ответ: .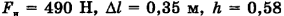

Эта задача взята со страницы подробного решения задач по физике, там теория и задачи по всем темам физики, можете посмотреть:

Физика — задачи с решениями и примерами

Возможно вам будут полезны ещё вот эти задачи:

Пример решения задачи №69. Однородный диск радиусом R = 0,2 м и массой m = 5 кг вращается вокруг оси, проходящей через его центр перпендикулярно плоскости диска. Зависимость угла поворота диска от времени дается уравнением , где . Вращению диска противодействует тормозящий момент сил трения . Определить величину касательной силы F, приложенной к ободу диска.

Пример решения задачи №70. При помощи укосины длиной м и растяжки длиной м подвешен груз весом Р = 3 кН (рис. 17-8). Расстояние между точками крепления укосины и растяжки к столбу м. Найти силы , с которыми груз действует на укосину и растяжку.

Пример решения задачи №73. К канату, концы которого закреплены на одной высоте, подвешены два груза массами m в 2 кг каждый. Точки подвеса грузов расположены на расстояниях r = 0,1 м от точек закрепления каната (рис. 17-10). Вследствие растяжения провисание каната составило h = 20 см. Найти силы натяжения участков каната.

Пример решения задачи №74. Определить давление р воды на стенку цилиндрического сосуда с диаметром основания D = 20 см на расстоянии l = 5 см от дна. Объем воды в сосуде V = 10 л, плотность воды