Измерение интенсивности множественной связи
Выше мы показали, что при проведении социально-экономических исследований часто изучаются связи между более чем двумя явлениями. Для оценки интенсивности такой связи используется коэффициент множественной корреляции (совокупный коэффициент корреляции), который характеризует тесноту связи одной из переменных с совокупностью других.
В качестве оценки интенсивности связи между результативным признаком 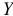 и совокупностью факторных признаков
и совокупностью факторных признаков
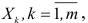
используется величина
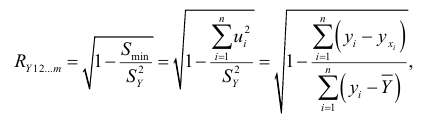
где 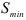 — наименьшее значение суммы
— наименьшее значение суммы
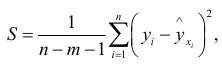
которая характеризует соответствие регрессии опытным данным, т.е. рассеяние значений 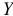 , которое возникает из-за случайностей и изменчивости прочих неучтенных факторов. Из формулы (2.10) видно, что чем меньше значение
, которое возникает из-за случайностей и изменчивости прочих неучтенных факторов. Из формулы (2.10) видно, что чем меньше значение 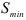 , тем меньше опытные данные
, тем меньше опытные данные 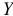 отклоняются от значений регрессии
отклоняются от значений регрессии
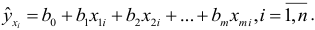
Величина 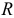 , вычисляемая по формуле (2.10), называется коэффициентом множественной корреляции (совокупным коэффициентом корреляции).
, вычисляемая по формуле (2.10), называется коэффициентом множественной корреляции (совокупным коэффициентом корреляции).
Средняя квадратичная ошибка коэффициента множественной корреляции определяется по формуле
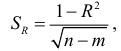
где 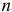 -чиcло наблюдений;
-чиcло наблюдений; 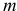 -число параметров уравнения регрессии.
-число параметров уравнения регрессии.
Используя значения параметров 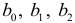 уравнения (2.4), найденных
уравнения (2.4), найденных
при решении системы нормальных уравнений (2.5), формулу (2.10) преобразуем к виду
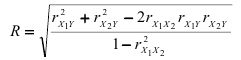
(см. [2, § 9.7]), где 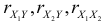 коэффициенты парной корреляции между переменными
коэффициенты парной корреляции между переменными
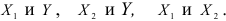
Коэффициент множественной корреляции удовлетворяет следующим свойствам:
1) его значения удовлетворяют неравенству 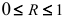 ;
;
2) если 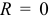 , то результативный признак
, то результативный признак 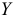 и факторные признаки не могут быть связаны линейной регрессионной зависимостью, хотя нелинейная зависимость может существовать;
и факторные признаки не могут быть связаны линейной регрессионной зависимостью, хотя нелинейная зависимость может существовать;
3) если 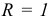 , то результативный признак
, то результативный признак 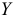 и факторные
и факторные 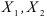 признаки связаны линейной функциональной зависимостью.
признаки связаны линейной функциональной зависимостью.
Из формулы (2.11) следует также, что если 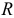 стремится к единице, то теснота линейной корреляционной зависимости между переменными
стремится к единице, то теснота линейной корреляционной зависимости между переменными 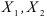 и
и 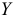 увеличивается, так как
увеличивается, так как 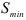 стремится при этом к нулю, т.е. опытные данные меньше отклоняются от значений регрессии.
стремится при этом к нулю, т.е. опытные данные меньше отклоняются от значений регрессии.
Об уровне тесноты множественной корреляционной связи между факторными признаками и результативным судят по значению множественного коэффициента корреляции 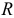 . Различают слабую
. Различают слабую 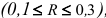 , умеренную
, умеренную 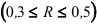 , заметную
, заметную 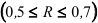 , тесную
, тесную 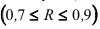 и весьма тесную
и весьма тесную 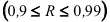 корреляционную связь.
корреляционную связь.
Отметим также, что с помощью коэффициента множественной корреляции нельзя сделать вывод о том, положительна или отрицательна корреляция между переменными. Только если все парные коэффициенты корреляции имеют один знак, можно установить характер связи между 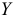 и
и 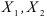 .
.
Из формулы (2.11) следует, что если коэффициент парной корреляции 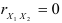 , т.е. если
, т.е. если 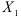 и
и 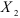 некоррелированы, то
некоррелированы, то 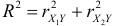 .
.
Это значит, что квадрат интенсивности связи между 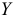 и
и 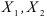 равен сумме квадратов интенсивности связи между
равен сумме квадратов интенсивности связи между 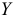 и
и 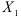 ,
, 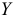 и
и 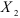 .
.
Коэффициент множественной корреляции можно вычислить через коэффициенты парной корреляции по формуле:
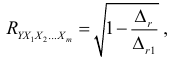
где

определитель матрицы парных коэффициентов корреляции,

определитель матрицы межфакторной корреляции.
Связь коэффициента множественной корреляции с нормированными коэффициентами регрессии 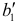 и
и 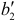 выражается формулой
выражается формулой
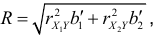
которая обобщается на случай любого конечного числа факторных признаков,
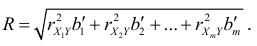
Как и в случае простой линейной регрессии, для установления того, какая часть общей дисперсии может быть объяснена зависимостью переменной 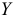 от переменных
от переменных 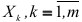 , вычисляют коэффициент множественной детерминации
, вычисляют коэффициент множественной детерминации
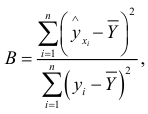
где
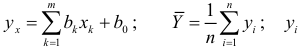
опытные данные. Его свойства и формула аналогичны свойствам и формуле простой линейной регрессии. Если 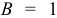 , то между
, то между 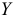 и
и 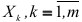 , существует линейная функциональная зависимость; если же
, существует линейная функциональная зависимость; если же 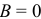 , то линейная зависимость отсутствует.
, то линейная зависимость отсутствует.
При пошаговом построении уравнения регрессии важно отметить изменение множественного коэффициента детерминации. Если при введении новых факторов в уравнение регрессии множественный коэффициент детерминации увеличивается, то вводимые факторы существенны. В противном случае вводимые факторы несущественны и их можно исключить из уравнения регрессии.
Если уравнение множественной регрессии содержит только два факторных признака 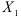 и
и 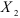 то его можно представить в виде
то его можно представить в виде
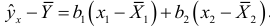
Возведем в квадрат обе части данного равенства и просуммируем все отклонения. Тогда, так как
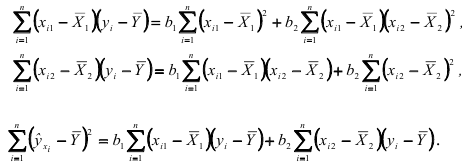
Подставив этот результат в формулу коэффициента множественной детерминации 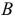 , приведем ее к виду
, приведем ее к виду
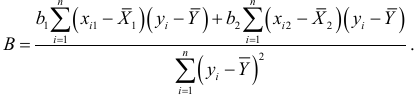
Итак, мы определили способы оценки тесноты связи одной переменной (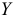 ) с совокупностью переменных
) с совокупностью переменных 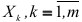 , включенных в анализ социально-экономических явлений. При этом следует отметить, что если переменные
, включенных в анализ социально-экономических явлений. При этом следует отметить, что если переменные 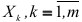 , коррелируют друг с другом, то на значение коэффициента парной корреляции между
, коррелируют друг с другом, то на значение коэффициента парной корреляции между 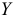 и
и 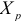 частично сказывается влияние других переменных. Вполне возможно, что корреляция между
частично сказывается влияние других переменных. Вполне возможно, что корреляция между 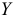 и
и 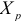 не прямая, а косвенная, возникающая вследствие воздействия других переменных
не прямая, а косвенная, возникающая вследствие воздействия других переменных 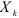 на
на 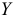 . Поэтому для определения интенсивности связи между
. Поэтому для определения интенсивности связи между 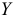 и
и 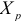 следует зафиксировать или исключить влияние других переменных
следует зафиксировать или исключить влияние других переменных 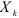 .
.
Интенсивность такой связи определяется с помощью коэффициентов частной корреляции. Исключенные переменные могут закрепляться как на средних уровнях, так и на уровнях, выбранных в соответствии с интересующими нас участками изменения переменных, между которыми определяется связь в чистой форме.
Изучим частную корреляцию в случае взаимосвязи трех переменных. Определим коэффициенты частной корреляции между переменными 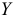 и
и 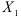 , при исключении влияния
, при исключении влияния 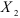 , а также частной корреляции между переменными
, а также частной корреляции между переменными 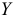 и
и 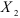 при исключении влияния
при исключении влияния 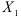 :
:
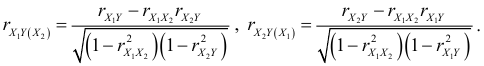
Как видно из приведенных формул, вычисление коэффициентов частной корреляции сводится к нахождению коэффициентов парной корреляции. Из формул (2.12) следует, что если 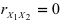 (переменные
(переменные 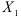 и
и 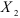 не коррелированы), то
не коррелированы), то 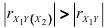 и
и 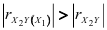 если же
если же 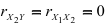 , то
, то 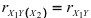 . Это означает, что с уменьшением взаимосвязи между факторами
. Это означает, что с уменьшением взаимосвязи между факторами 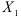 и
и 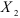 коэффициент частной корреляции по сравнению с соответствующим коэффициентом парной корреляции не убывает, причем увеличение коэффициентов частной корреляции тем сильнее, чем больше
коэффициент частной корреляции по сравнению с соответствующим коэффициентом парной корреляции не убывает, причем увеличение коэффициентов частной корреляции тем сильнее, чем больше 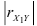 или
или 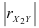 .
.
Кроме того, при 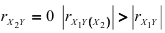 , а при
, а при 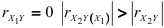 если же
если же 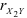 и
и 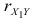 имеют противоположные знаки, то всегда
имеют противоположные знаки, то всегда 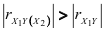 . Отметим, что коэффициент множественной корреляции также связан с частными коэффициентами корреляции по формуле
. Отметим, что коэффициент множественной корреляции также связан с частными коэффициентами корреляции по формуле
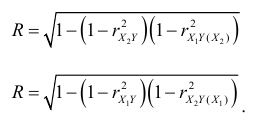
Обобщим формулы (2.12) на любое число факторных признаков. Для этого воспользуемся формулами, связывающими коэффициенты частной и парной корреляций с коэффициентами частной регрессии:
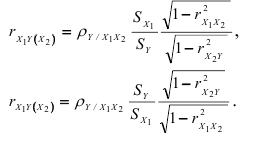
Перемножив правые и левые части приведенных формул, получим:
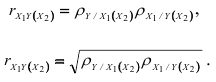
Обобщая формулу (2.13), можно записать:
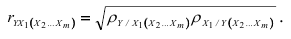
Аналогично можно обобщить и формулы (2.12):
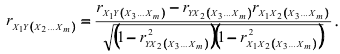
Как видно из формулы (2.14), вычисление коэффициентов частной корреляции порядка 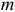 сводится к вычислению коэффициентов частной корреляции порядка
сводится к вычислению коэффициентов частной корреляции порядка 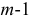 . Поэтому применение формулы (2.14) предполагает знание коэффициентов парной корреляции, что позволяет вычислять коэффициенты частной корреляции, которые в свою очередь дают возможность вычислять коэффициенты частной корреляции более высокого порядка.
. Поэтому применение формулы (2.14) предполагает знание коэффициентов парной корреляции, что позволяет вычислять коэффициенты частной корреляции, которые в свою очередь дают возможность вычислять коэффициенты частной корреляции более высокого порядка.
В множественном регрессионном анализе определяют часть из тех изменений, которые в данном явлении зависят от одного факторного признака при исключении влияния остальных факторных признаков, рассматриваемых в регрессии. Для этого используется коэффициент частной детерминации.
Остановимся на случае линейной зависимости результативного признака 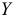 от факторных признаков
от факторных признаков 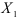 и
и 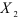 .
.
Для оценки части вариации 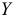 , объясняемой вариацией фактора
, объясняемой вариацией фактора 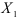 , при исключении влияния
, при исключении влияния 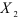 , определим формулы коэффициента частной детерминации
, определим формулы коэффициента частной детерминации 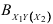 по данным, из которых исключены значения фактора
по данным, из которых исключены значения фактора 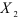 :
:
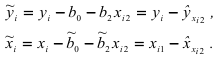
Используя формулу
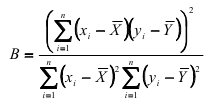
и учитывая, что
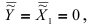
получаем выражение коэффициента частной детерминации:
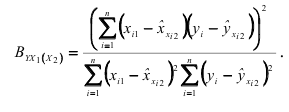
Выполнив элементарные преобразования, приведем это выражение к виду
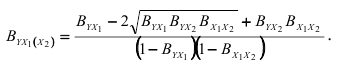
Из формулы (2.15) следует, что коэффициент частной детерминации вычисляется по коэффициентам парной детерминации. Эта формула позволяет устанавливать часть вариации, обусловленной зависимостью результативного признака 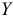 от фактора
от фактора 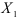 при исключении влияния
при исключении влияния 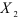 .
.
Укажем формулы, связывающие коэффициенты множественной и частной корреляций, регрессии и детерминации. Между коэффициентами множественной корреляции 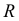 и детерминации
и детерминации 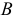 существует следующее соотношение:
существует следующее соотношение:
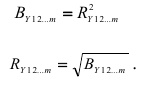
Такие же соотношения справедливы и для коэффициентов частной корреляции и частной детерминации. Например,
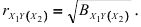
Коэффициент множественной детерминации равен сумме коэффициентов парной детерминации, если переменные 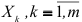 попарно не коррелированы,
попарно не коррелированы,
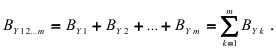
Кроме того, справедливо следующее соотношение между коэффициентами частной детерминации и регрессии: