Оглавление:





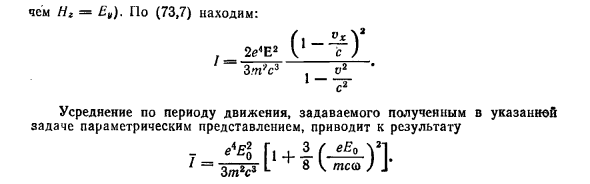

Излучение быстро движущегося заряда
- Излучение быстро движущегося заряда. Тогда заряженные частицы Скорость не маленькая по сравнению со скоростью света. Формула §67, оцененная в предположении v <C c, в данном случае не применима напрямую.
Тем не менее, вы можете рассмотреть частицы в системе отсчета, которые в настоящее время являются стационарными. В этой системе отсчета четко применяется приведенная выше формула (это привлекает внимание к тому факту, что это может быть сделано только с одной движущейся частицей.
показанной системе отсчета частица излучает энергию в течение времени Людмила Фирмаль
Для множества частиц, вообще говоря, все они Ни одна система отсчета не является стационарной одновременно). Таким образом, в dt. d s = ^ w2dt (73,1) Где w — ускорение частицы в той же системе (согласно уравнению (67.9)). Суммарные импульсы, излучаемые им в рассматриваемой системе отсчета, равны нулю dP = 0. (73,2)
Фактически импульсное излучение определяется как интеграл плотности потока импульсов в поле излучения на замкнутой поверхности, окружающей частицу. Однако из-за симметрии дипольного излучения импульсы, унесенные в противоположном направлении, имеют одинаковую величину и противоположные направления.
- Следовательно, указанный интеграл исчезает так же, как и ноль. Перепишите, чтобы перейти на любую справочную систему Четырехмерные формулы (73.1) и (73.2). Легко увидеть «4-импульсное излучение» dPl dpi = — ^ dx * = —- tfds. (73,3) 3 с дс д с 3 с дс дс Фактически, в системе отсчета, где частица неподвижна, пространственная составляющая 4 скорости u равна нулю, дук дук w2 1T ^ a a ——— = -поэтому пространственная составляющая a ± J дс дс с4 ’
Временные вещи дают равенство (73.1). Общее излучение 4 импульса при прохождении частиц Результирующее электромагнитное поле равно интегралу уравнения (73.3). DR * = dxi (73,4) 3 секунды J ds ds Перепишите эту формулу в другую форму, чтобы выразить 4 ускорения Дул / дс с тензором внешнего электромагнитного поля с помощью Общее уравнение движения (23.4): Клук ^ 771 я t s- = -FHu. И дс
Компонент времени уравнения Людмила Фирмаль
Тогда вы получите AP1 = второй 3 м В j {F klul) {Fkmum) dx \ (73,5) (73.4) или (73.5) дает слово Высвобождение энергии КАК. Если вы выражаете 4-мерную величину с 3-мерной величиной, это делается следующим образом. о A <y = ^ (W 5) 3c3 J (1-w 2 / s) — объектно-ориентированное (W = ускорение v-частиц) или через внешнее электричество
И магнитное поле: 7 {E +; [vH]} 2-1 (E v) 2 A ^ = / / A- / = ‘<73’7> -оо Уравнение для полного излучения импульса отличается на дополнительный множитель v под знаком интеграла. Из уравнения (73.7) видно, что оно близко к следующей скорости. В случае света полное излучение энергии в единицу времени зависит в основном от скорости как (1-v2 / c2) ~ \ i.
Другими словами, он пропорционален квадрату энергии движущихся частиц. Единственное исключение — движение в электрическом поле, параллельном направлению электрического поля. В этом случае коэффициент (1 — v2 / s?) В знаменателе оно уменьшается на тот же коэффициент, что и числитель, а излучение не зависит от энергии частицы.
Наконец, мы обсудим проблему углового распределения. Излучение от быстро движущихся частиц. Для решения этой проблемы удобно использовать формулу Лиенара-Вихерта в поле (63.8), (63.9). На больших расстояниях необходимо сохранять только формулу с нижним порядком 1 / R (второй член в формуле (63.8)).
Введение вектора направления единицы n Излучение (R = PD), получить уравнение = _e _ [«[(» -v / c) w]] = c2 I (1-n v / c) 3 ‘L J’ V} Здесь все величины в правой части уравнения берутся в момент задержки t ‘= t-R / c. Интенсивность излучения телесного угла составляет = = -E 2R2. Откройте квадрат E2, 4 7 г = _ e ^ _Γ2 (nw) (vw) w 2 _ (l- ^ 2 / c2) (nw) 2 \ 47Gs3 [с (1-вн / с) 5 (1-вн / с) 4 (1-вн / с) 6 Дж (73,9)
При определении общего углового распределения Необходимо интегрировать интенсивность во времени, излучение в течение времени, которое проходит заряд. Должен помнить Интегрируемое выражение является функцией, поэтому необходимо Написать dt = 0 dt ‘= (l- ™) dt’ (73.10) (См. (63.6)), то интегрирование выполняется напрямую На самом деле по DTF.
Следовательно, существует следующая формула для суммарного излучения на элемент телесного угла do. = l do f (2 («wKvw> w- _ a-a dy, 47gs J [c (l-vn / c) (1-vn / c) (1-vn / c) J (73,11) Как видно из (73.9), угловое распределение излучения в общем случае довольно сложное. Гиперрелятивистский случай (1-v / c 1) имеет особенности Если в знаменателе существует большая разница 1-v н / с Разные члены этого выражения.
Другими словами, интенсивность увеличивается в узком угловом диапазоне, где разница 1-vn / c мала. Покажите букву под небольшим углом между n и v, 11 —- v a cos in ^ 11 —— v- -I — Q-2; с с 2 Эта разница мала 1-v / c) для b ~ y / l-v / c, или же ~ Y1-Ј. (73,12) Поэтому суперрелятивистские частицы излучают в направлении их движения, главным образом в угловом диапазоне (73.12).
Вокруг скорости. Также для любой скорости и ускорения У частицы всегда есть два направления, в которых интенсивность излучения исчезает. Это направления, в которых вектор n-v / c параллелен вектору w. Таким образом, le (73.8) исчезает (см. также вопрос 2 в конце раздела).
Наконец, напишите более простое выражение. Прогулка в двух особых случаях (73,9). Если скорость частицы и ускорение параллельны, H = c2R (1-v н / с) 3 И сила d l = — ^ j-w * s ™ 2 (> do. (73.13) 47G (1- (v / c) COS 0) Естественно симметрично вокруг направления соединения v и w исчезают в направлении, противоположном направлению вдоль (b = 0) (‘9 = 7 г) скорость.
В гиперрелятивистском случае интенсивность как функция от in имеет двойной резкий максимум в области. (73.12) «Окунитесь» в ноль с β = 0. Если скорость и ускорение перпендикулярны друг другу, С (73,9) 2 2 7 часов дл = —- г 47G с (1-v2 / s2) cos2 sin2 (p (1- (v / c) cos O) 4 (1- (v / c) COS0) 6 До, (73,14) Где b — это угол между n и v, а <p — азимут. Угол вектора n между плоскостью, проходящей через v и w.
Это Интенсивность только симметрична относительно плоскости vw Исчезают в двух направлениях на этом самолете, Сформируйте скорость под углом = arccos (v / c). Задача 1. Определить суммарное излучение релятивистских частиц по заряду ei. Летите на расстоянии удара p в кулоновом поле с фиксированным центром (потенциал ip = / g). Решения.
При прохождении через поле релятивистские частицы почти не отклоняются 1). Поэтому в (73.7) можно рассмотреть постоянную скорости v. В зависимости от поля в терминах частиц B2G _ B2G Е g- (p2 + L2) 3/2 ’ Где x = vt, y = p. (73.7) выполнить интегрирование по времени, Мы получаем = 7r ^ e2 4s2-y2 12 м2c3p3v c2-v2 2. Определите интенсивно направление исчезновения Излучение движущихся частиц. Решения.
Из геометрической структуры (рисунок 15) мы видим, что требуемое направление n находится в плоскости, которая проходит через. Вырежьте и определите v и w, сформируйте направление w и угол% От отношений грех *: ■ сма, Где а — угол между v и w. 3. Определить интенсивность заряженного излучения Неподвижная частица, которая движется в поле плоско поляризованных электромагнитных волн.
Решения. По результатам части проблемы 3§48 ца движется по кругу, каждая скорость Момент времени, параллельный и перпендикулярный полю H Поле Э. ее кинетическая энергия = c y p 2 + ha2 c2 = cj 15 -v2 / c2 (Обозначение проблемы указано). Используйте формулу (73.7), чтобы найти силу.
Радиационная мощность: 1 = 2e4 E 2_ 2e4Eg с / в-1 с т 33 т2с3 1 + / EP \ 21 \ mcoj ‘\ 4. То же самое относится и к области линейной поляризации. Решения. В соответствии с результатом § 48 вопрос 2 вызовет движение В плоскости xy, проходящей через направление распространения волны (Ось X) и направление поля E (ось y), поле H ориентировано вдоль оси z (и Hz = Ey). По (73,7) 2e4E 2 (1-vx / cf Zt2s3 1-v2 / s2 Усреднение по периоду упражнений, заданному параметрическим представлением, полученным с указанной задачей, приводит к результату Я = 3 тонны 1 + -3 / EP \ 21 \ mcoj ‘\
Смотрите также:
| Квадрупольное и магнитно-дипольное излучения | Магнито-тормозное излучение |
| Поле излучения на близких расстояниях | Торможение излучением |

