Изгиб с растяжением (сжатием)
Изгиб с осевым растяжением (сжатием) прямого бруса. В общем случае на брус могут действовать как поперечные, так и продольные нагрузки (рис. 2.52, а). Такое нагружение приводит к появлению в поперечных сечениях изгибающих моментов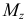 
и 
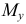, поперечных сил 
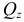и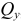 
, а также продольной силы 
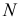(рис. 2.52, б). Здесь имеет место сочетание косого изгиба с осевым растяжением.
Продольная сила 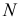изменит напряжения в каждой точке сечения на величину
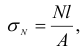
где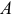 
— площадь поперечного сечения.
Учитывая указанное обстоятельство, а также формулу (2.98), получаем следующее выражение для определения нормального напряжения в произвольной точке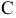 
сечения:
Изгибающие моменты, продольную силу, а также координаты точки, в которой определяют напряжения, необходимо подставлять в зависимость (2.107) со своими знаками.
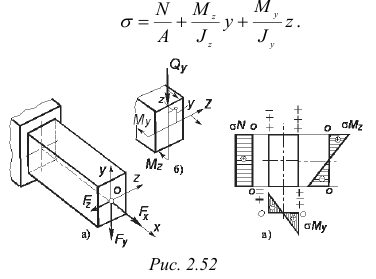
Так как напряженное состояние в опасной точке можно считать линейным (не учитывается влияние касательных напряжений), то условие прочности имеет следующий вид:
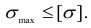
Если сечение имеет две оси симметрии и выступающие углы, то опасной будет одна из угловых точек. Напряжение в этой точке определяется либо по формуле
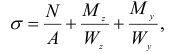
либо по формуле (2.107). Знаки перед слагаемыми в правой части зависимости (2.109) устанавливают путем анализа распределения напряжений по поперечному сечению бруса (рис. 2.52, в).
Внецентренное растяжение (сжатие) прямого бруса. Внецентренное растяжение (сжатие) характеризуется наличием силы, линия действия которой параллельна оси бруса, но не совпадает с ней (рис. 2.53, а).
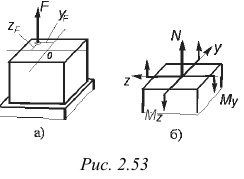
Координаты точки приложения силы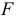 
обозначим через 
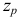и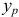 
. Отметим, что направления координатных осе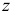й 
и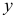 
всегда следует выбирать такими, чтобы 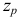и 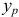были положительными.
Применив метод сечений, найдем, что в любом поперечном сечении бруса действуют изгибающие моменты
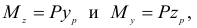
а также продольная сила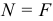 
(рис. 2.53, б). Нетрудно заметить, что здесь, как и в рассмотренном выше случае, имеет место совместное действие косого изгиба с осевым растяжением (сжатием). А потому формула для определения напряжения в произвольной точке сечения с координатам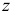и и 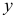будет аналогична (2.107), т. е.
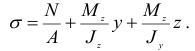
Для сечения с двумя осями симметрии максимальные напряжения определяют по формуле (2.109).
Преобразуем выражение (2.110), подставляя вместо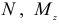 
и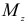 
их значения:
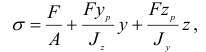
или
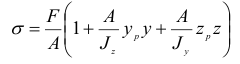
Так как отношения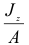 
и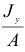 
представляют собой квадраты радиусов инерции сечения относительно осе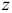й 
и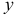 
соответственно, то, обозначив их через 
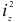и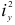 
, имеем
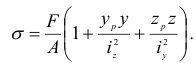
Распространяя полученную зависимость на случай действия сжимающей силы 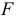представим формулу (2.111) в ее общем виде:
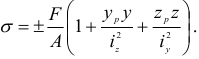
Подчеркнем еще раз, что знак перед правой частью уравнения (2.112) определяется характером действующей силы: при растяжении ставится знак плюс, при сжатии — минус. Координаты 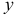и 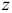произвольной точки подставляют со своими знаками.
Положение опасной точки сечения можно найти, построив вначале нейтральную линию. Уравнение нейтральной линии получим, положив в формуле (2.112)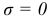 
и обозначив координаты точек на этой лини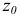и 
и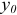 
. Тогда, учитывая, что 
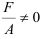, имеем
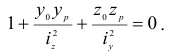
Из полученного уравнения следует, что нейтральная линия никогда не проходит через начало координат, отсекая на осях 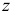и 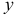отрезки, равные соответственно
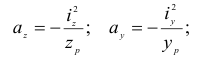
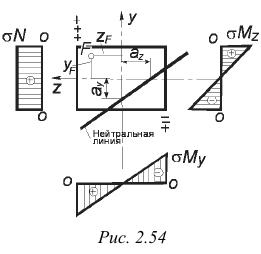
Примерное положение нейтральной линии для рассмотренного случая внецентренного растяжения бруса показано на рис. 2.54. Из этого же рисунка видно, что в растянутой и сжатой зонах сечения находятся наиболее напряженные точки и 
(в точке -максимальное растягивающее напряжение, в точке 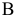— максимальное напряжение сжатия). Полезно запомнить, что точка с наибольшим по абсолютному значению напряжением всегда расположена в одном квадранте с точкой приложения силы 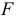, а знак напряжения в этой точке соответствует характеру действующей силы. Условие прочности записывается так:
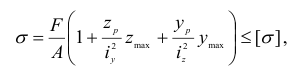
Здесь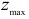 
и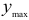 
— координаты точки, наиболее удаленной от нейтральной линии.
Эта теория взята со страницы лекций по предмету «прикладная механика»:
Возможно эти страницы вам будут полезны:
| Теория прочности. Основные понятия |
| Косой изгиб: определение, пример, формулы |
| Видимые местные напряжения |
| Изгиб с кручением: определение и формулы |
