Изгиб с кручением
При изгибе с кручением в поперечных сечениях стержня появляются изгибающий и крутящий моменты. На кручение с изгибом работают элементы пространственных конструкций, валы машин, винтовые пружины и др.
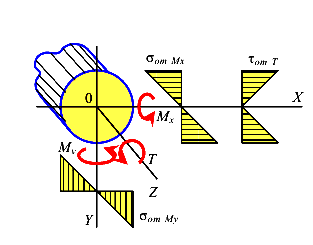
Рассмотрим стержень круглого сечения. Учитывая принцип независимости действия сил, напряжения в произвольной точке сечения равны сумме напряжений от кручения и от изгиба
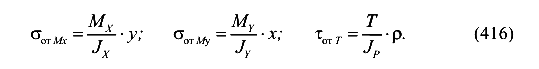
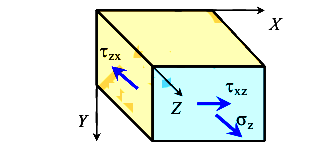
Анализ эпюр показывает, что опасная точка, обозначим ее буквой S, располагается на контуре сечения. Выделим около точки S элементарный параллелепипед (рис. 127).
круглого сечения
Очевидно, что выделенный элемент находится в условиях плоского напряженного состояния, так как площадки с нормалью У свободны от напряжений. Поэтому главные напряжения могут быть вычислены по известной формуле
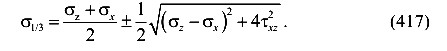
Так как 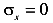 , имеем
, имеем
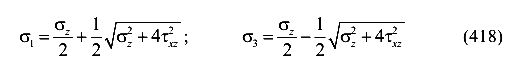
По 3-й теории прочности условие наступления предельного состояния имеет вид

Подставим выражения для напряжений (418) в условие прочности
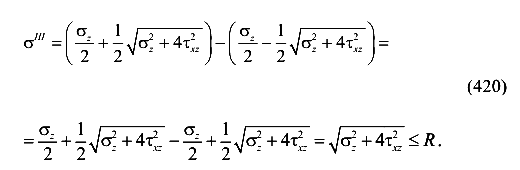
Подставим выражения (416) для напряжений в опасной точке S
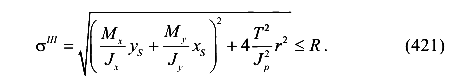
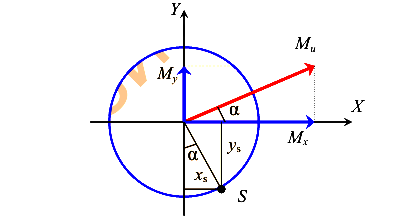
Установим связь между моментами и координатами точки S. Для этого используем элементы векторной алгебры (рис. 128).
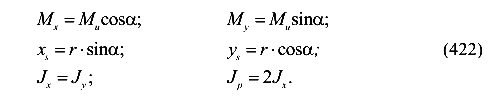
После подстановки (422) в выражение (421) получим
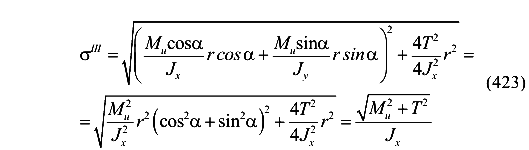
И, окончательно, для третьей теории прочности имеем

где
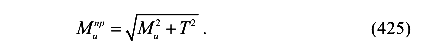
По четвертой теории прочности имеем (без вывода)

где
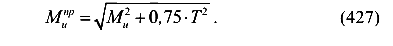
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:
| Порядок расчета внецентренно сжатой колонны |
| Изгиб с растяжением или сжатием |
| Расчет пространственного ломаного стержни |
| Устойчивость сжатых стержней |

