Изгиб с кручением
В конструкциях различных механизмов очень часто встречаются детали, работающие на совместное действие изгиба и кручения. Характерным примером таких деталей являются валы самых разнообразных устройств.
Силы, которые передаются на вал механизма, в общем случае приводят к появлению в поперечных сечениях вала крутящего момента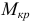 
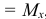, изгибающих моментов 
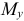и 
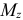; а также поперечных сил 
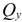и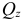 
. Под действием указанных силовых факторов в сечениях возникают нормальные (от изгиба) и касательные (от изгиба и кручения) напряжения. Величиной касательных напряжений от изгиба обычно пренебрегают, поскольку она незначительна по сравнению с величиной касательных напряжений от кручения. Поэтому рассматривают фактически сочетание кручения с чистым изгибом.
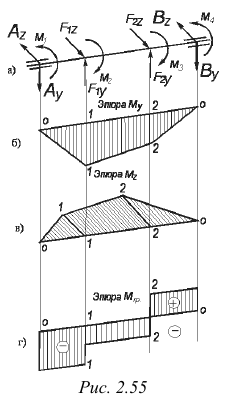
Рассмотрим вал круглого поперечного сечения (рис. 2.55, а). Используя принцип независимости действия сил, строим эпюры изгибающих моментов от нагрузок, действующих в вертикальной и горизонтальной плоскостях (рис. 2.55, б и б), а также эпюру крутящих моментов (рис. 2.55, г). Сопоставляя полученные эпюры, находим, что опасными являются сечения 1-1 и 2-2.
В каждом сечении круглого вала имеет место прямой изгиб от действия результирующего изгибающего момента.
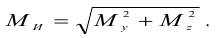
Нормальные напряжения от этого момента достигают наибольших значений в крайних волокнах вала и определяются по формуле
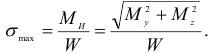
В любой точке контура поперечного сечения вала действуют также максимальные касательные напряжения от кручения, связанные с величиной крутящего момента соотношением
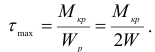
В формулах (2.115) и (2.116)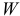 
— осевой момент сопротивления сечения вала.
Найдем наиболее напряженные точки в одном из опасных сечений вала (например, в сечении 1-1). Такими точками, очевидно, являются точк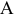и 
и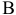 
, наиболее удаленные от нейтральной линии (рис. 2.56).
Положение нейтральной линии в данном случае найти нетрудно. Воспользовавшись формулой (2.101) и имея в виду, что для круглого сечения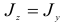 
, получим 
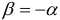, где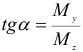 
.
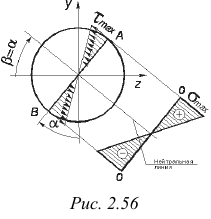
На рис. 2.56 показаны суммарная эпюра нормальных напряжений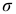 
от действия результирующего изгибающего момента 
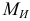и эпюра касательных напряжений 
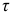от кручения. Исследуем напряженное состояние в одной из опасных точек сечения (например, в точке ).
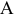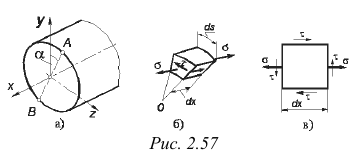
В окрестности точки 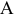(рис. 2.57, а) выделим элементарный объем (рис. 2.57, б). По четырем его граням ; действуют касательные напряжения 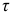, а по двум граням, параллельным плоскости поперечного сечения, — также нормальные напряжения 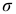(в данном случае — растягивающие). Остальные грани от напряжений свободны. Таким образом, при изгибе с кручением элемент в опасной точке находится в плоском напряженном состоянии (рис. 2.57, в).
Для определения величин главных напряжений применяют зависимость (2.25), а прочность вала в опасном сечении проверяют по формулам приемлемых теорий прочности.
Воспользуемся, например, условием прочности (2.96), исходя из третьей теории:
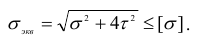
Подставив в это условие выражения (2.115) и (2.116) для напряжени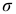й и 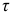, получим
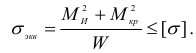
Если исходить из четвертой теории прочности, то согласно условию (2.96)
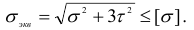
Осуществив подстановки, аналогичные предыдущим, имеем
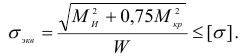
Условия прочности (2.117) и (2.118) можно заменить одной формулой
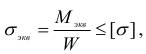
где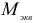 
— эквивалентный (приведенный) момент. Для третьей теории прочности
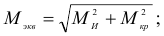
для четвертой теории прочности
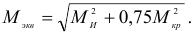
Заметим, что все приведенные формулы применимы и для расчета валов кольцевого сечения.
При проверочных расчетах, когда диаметр вала известен, коэффициент запаса прочности
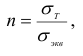
где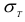 
— предел текучести.
По третьей теории прочности значение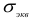 
определяется выражением (2.94). Для этого случая
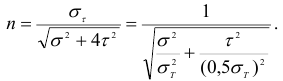
В соответствии с третьей теорией
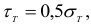
поэтому
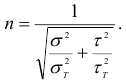
Формула (2.121) после преобразований принимает вид
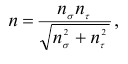
где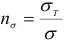 
— коэффициент запаса прочности по нормальным напряжениям; 
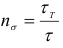— коэффициент запаса прочности по касательным напряжениям.
Следует отметить, что зависимости (2.121) и (2.122) остаются в силе и для четвертой теории прочности, только здесь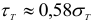 
.
Эта теория взята со страницы лекций по предмету «прикладная механика»:
Возможно эти страницы вам будут полезны:
| Косой изгиб: определение, пример, формулы |
| Изгиб с растяжением (сжатием) |
| Концентрация напряжений определение и формулы |
| Видимые местные напряжения |
