Оглавление:




Изгиб кривого бруса
- Изгиб кривой рельса. Если ось стержня изогнута, но размер поперечного сечения меньше радиуса кривизны, можно использовать ту же формулу, что и для прямого стержня. Если размер сечения сопоставим с радиусом кривизны, то влияние кривизны сильно повлияет на распределение напряжений. Когда
мы рассматриваем задачу изгиба стержня значительной кривизны, то специальный расчет, что ось представляет собой дугу окружности, поперечное сечение симметрично относительно плоскости оси, а изгибающая сила действует в этой плоскости, основан на 1
гипотезе. Плоский участок, перпендикулярный оси стержня, остается плоским Людмила Фирмаль
и перпендикулярным кривой оси после деформации. 2. Ось проходит через центр кривизны, а цилиндрическая плоскость, перпендикулярная плоскости оси стержня, является свободной от напряжений. Первая гипотеза справедлива именно в случае чистого изгиба, то есть когда он изгибается парой сил. Вторая
гипотеза предполагает, что круговые волокна, которые стержни могут мысленно разделить, имеют 246 изгибающих напряжений. IX Не взаимодействуйте друг с другом. Это явно невозможно: растянутые и изогнутые волокна находятся в равновесии только из-за реакции соседних волокон, которую можно сравнить с той, что показана на рисунке. 168-веревка, наброшенная на цилиндр сверху.
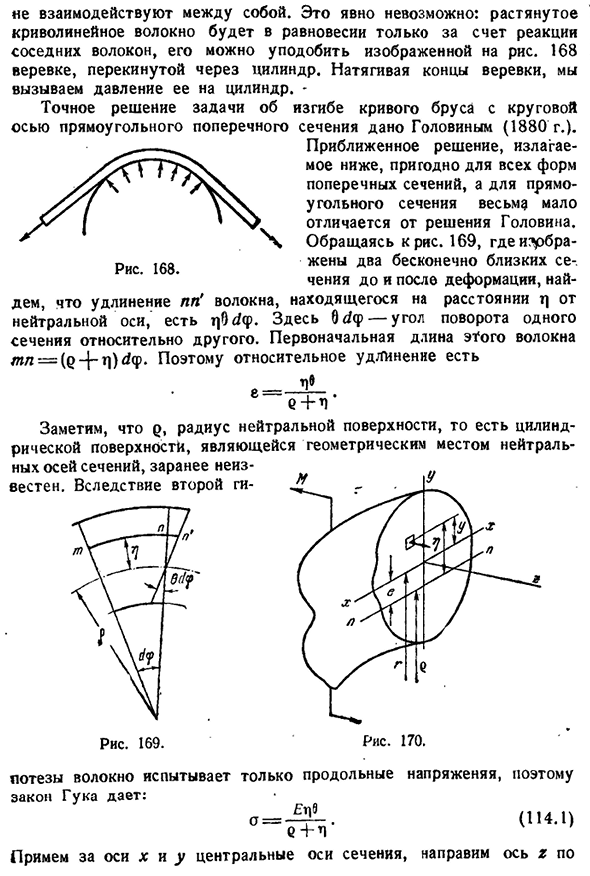
- Если вы потянете за конец веревки, на цилиндр будет давить давление. — Точное решение задачи изгиба криволинейных балок с круговой осью прямоугольного сечения дано Головиным (1880). _ Приведенное ниже приближенное решение подходит для всех форм поперечного сечения, а прямоугольное сечение мало отличается от решения Головина. ’ Обратимся к рис. 169, где показаны два
бесконечно близких участка до и после деформации, протягиваем волокно PP на расстояние q от одного волокна нейтральной оси q8dq, где 0dtp-угол поворота участка относительно другого. Это/Yal=(e-}-t]) ^ f исходной длины. Так же как и расширение ми== Л? _ # С+Л Следует отметить, что Q, радиус нейтральной поверхности, то есть кристаллической поверхности, является геометрическим положением нейтральной оси сечения, заранее не известным.
Для второго ги- Цилиндр- Волокна испытывают в туалете только Людмила Фирмаль
продольную деформацию, которую дает закон крючка: Так… £г]9 СТ » с+ * г Возьмите центральные оси x и y и укажите на ось z (114.1)§ 114] изгиб изогнутой балки 247 Когда поперечное сечение сделано, формула проекции для оси g (все силы на рисунке) сделана. 170). В случае силы мы получаем: чистый изгиб здесь включает только внутреннюю сторону Дж Д ф=0. Г И так оно и есть. (114.2} Формула (114.2) поможет в дальнейшем найти расположение нейтральной оси. Обратите внимание, что на данный момент, если Q больше размера
секции, значение g игнорируется в знаменателе: Итак, в этом случае нейтральная ось проходит через центр тяжести. В общем случае нейтральная ось смещена относительно центра тяжести. Теперь составим уравнение момента на нейтральной оси. Получаем: M-J r|d f=O. (114.3} Ф Но Второй Интеграл равен нулю по формуле (114.2), а первый Интеграл-статический момент площади поперечного сечения относительно нейтральной оси: Или] D F=EP. Принимая это во внимание, получим из уравнения (114.3) Если я подставлю значение e9n выражение (114.1) найдено, я получу его? М и Е? С+П’ (114.4} Это основная формула для нахождения нормального напряжения при чистом изгибе гибочной балки.
Если изгиб производится силой, которая вызывает тангенциальное напряжение при растяжении или сжатии сечения, то уравнение (114.4) является наиболее важным*248 изгибающее напряжение (глава IX). » Часть стресса. График распределения напряжений в разрезе представляет собой гиперболу, а не прямую линию, как стержень с прямой осью. Чтобы воспользоваться формулой (114.4), нам не хватает одного: мы все еще не знаем положения нейтральной оси
Смотрите также:
| Несущая способность внецентренно сжатого стержня | Нахождение нейтральной осн в кривом стержне |
| Расчет составных балок | Дифференциальное уравнение изогнутой оси |

