Оглавление:






Изгиб балок, материал которых не следует закону гука
- Изгиб балок, которые не подчиняются законам их материала крючьями Предыдущие расчеты на прочность и жесткость при изгибе были основаны на гипотезе закона крюка и плоского сечения с одинаковым модулем упругости при растяжении и сжатии., Закон крюка действует до тех пор, пока напряжение не превышает определенного значения, называемого пределом пропорциональности, и в некоторых случаях прочность рассчитывается при более высоком напряжении с учетом пластической деформации кроме того, зависимость напряжения
и деформации во многих материалах нелинейна в диапазоне упругости. В некоторых материалах модуль упругости растяжения и сжатия отличается в соответствии с законом крюка. Таким образом, недавний расчет Во всех этих случаях 325прочность приобретает все большее значение. Прочностные расчеты, учитывающие пластическую деформацию, рассматриваются в Главе 18. Показано, что зависимость между напряжением и деформацией различна при растяжении и сжатии. © © © г, Б, Триста дюжин риса Также рассмотрим случай при изгибе с различными упругими модулями для растяжения и сжатия. Эксперимент показывает,
что в этих случаях гипотеза плоского поперечного сечения справедлива. Людмила Фирмаль
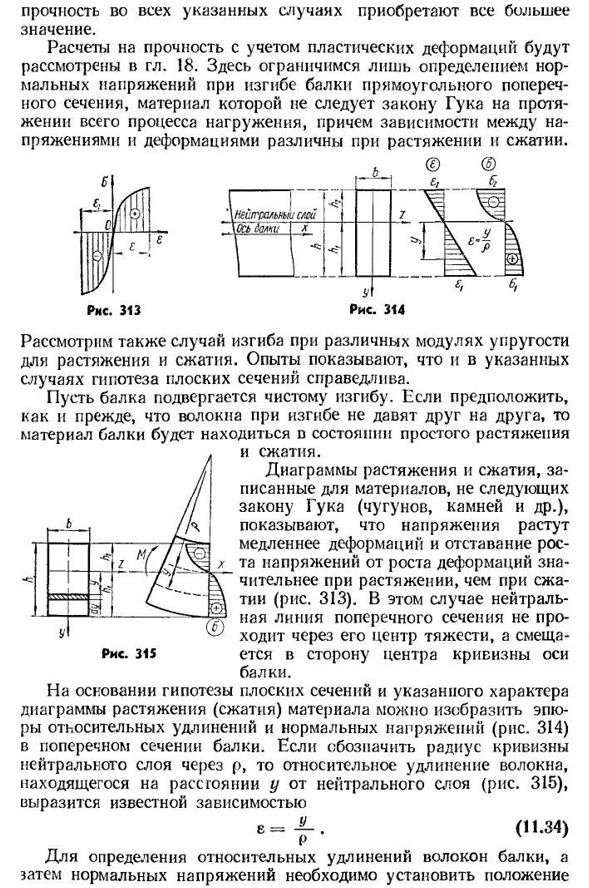
Аккуратно согните балку. Как и прежде, предполагая, что волокна в изгибе не прижимаются друг к другу, материал балок будет находиться в состоянии простого растяжения и сжатия. Диаграммы растяжения и сжатия, записанные для материалов, не подчиняющихся законам крюка (чугун, камень и др.). Это означает, что напряжение становится медленнее, чем деформация, показано, что задержка роста напряжения за счет роста деформации больше при растяжении, чем при сжатии. 313). В этом случае нейтральная линия поперечного сечения смещается не через его центр тяжести, а в сторону центра кривизны оси балки. Основываясь на гипотезах
плоских сечений и заданных свойствах диаграмм растяжения (сжатия) материала, можно изобразить график относительного удлинения и нормального напряжения(рис. 314) в поперечном сечении балки. Если обозначить радиус кривизны нейтрального слоя через p, то относительное удлинение волокон находится на некотором расстоянии от нейтрального слоя(рис. 315) представлена известной зависимостью e=f. (H. 34)необходимо определить относительное удлинение пучка волокна и затем
- установить нормальное давление, положение 326 сечение нейтральной оси, связь между радиусом кривизны нейтрального слоя и деформацией и напряжением представлена аналитически или графически. Нарисуйте поперечное сечение балки перпендикулярно ее оси. При изгибе балки с помощью пары сил внутренние упругие силы поперечного сечения также должны быть сопряжены, и поэтому требуется проекция вертикальной силы на ось x (рис. 315) равно нулю, а их моменты относительно нейтральной оси z равны изгибающему моменту. Таким образом, мы получаем следующее S X=f odF=O F в МГ=(oydF-м ф Каждый б я opdy-\ря) Kdy(’ Два уравнения статики: =0. (11.35 утра) =0;(11.36) (11.37)) Начиная с DF-bdy, Отчет в. ) (bi h\b и opydy+j Gcnydy) во многих материалах соотношение между напряжением и деформацией при растяжении и сжатии может быть
выражено с достаточной точностью степенным законом Р^ре^СД — ^СЖ » (11.38) Где/?РД СД, P и T значение ep=LRO характеризует физические свойства материала. Учитывая уравнение относительной деформации (11.34), из зависимости (11.38), оно представляет нормальное напряжение следующим образом: т. rn Л Тонны ■(11.39) О Р Эти зависимости и уравнения (11.36) и(11.37) позволяют определить положение нейтральной оси, величину радиуса кривизны, а также напряжения ОП и ОСЖ. Подставляя выражение (11.39)в выражение (11.36), вы получаете следующее выражение р ч’ «л»» Отчет 1-0. И после завершения интеграции, мы имеем Я /г. ———— г-г. 1tn4-1 п П+1 / Г2=0. (11.40 утра) 327 тогда, если мы заменим выражение (11.39) на выражение (11.37)、 =М, — ОО ’ на И после интеграции, мы получаем Имея в виду Hi4-L2=/g, находим p и L2 из уравнений (11.40) и (11.41), затем уравнение (11.39) —
напряжение или hi, osj. Можно также решить обратную задачу, что максимально допустимый изгибающий момент определяется допустимым Людмила Фирмаль
растягивающим напряжением|или 1 или сжатием 1ocj1. Для решения этой задачи используются формулы (hi и h2) для расчета расстояния от нейтрального слоя hi и hi балки в h, предела прочности на растяжение в крайних волокнах балки и расстояния от нейтрального слоя.). (11.42) Исходя из этих формул (11.40) и (11.41), представим в следующем виде: GP (11.43)) (11.44) Кроме того, из выражения (11.42) это выглядит следующим образом (11.45)) Уравнение Hi+h2 — = h в дополнение к последним трем уравнениям, для вычисления допустимых значений положения нейтральной оси от допустимого напряжения[A4]или 1£R. график нормальных напряжений сечения балки в этом случае показан на рисунке. 316. Для волокон, находящихся на расстоянии y, от нейтрального слоя в зоне натяжения N происходит сжатие Я осдж — Из равенства (11.36), это выглядит так (11.46) (11.47) Подставляя эту формулу (11.46)
вместо Or и osj, вы получаете (11.48)) Куда деваться после консолидации и сокращения Или Рассматривая hi+h2= * =L, находим / hg£Р(11.50)Б~+■В (11.49) Один. 2Р Таким образом, определяется положение нейтрального SSI. Теперь мы находим напряжение в крайних волокнах пучка в области удлинения или в области сжатия asj. Из диаграммы напряжений полное напряжение Nv в зоне растяжения и сила сжатия в зоне сжатия поперечного сечения получены по следующему уравнению: (11.51)) 2/2 Эти силы действуют на расстоянии g-fti и h2 от нейтрального слоя. Поскольку сила в поперечном сечении сводится к паре сил, L7r=L/SJ. Изгибающий момент можно записать в виде пары моментов силы, равной
напряжению 329 пар плеч-к-плеча прочности на сжатие: 2 фута; M=Ncxt — ^ — h. Даны формулы(11.51) и (11.50)、 VEP+ / E FW Л4=о VBH ’ ч=°п^2. Три. > (11.52) (11.53)) Откуда з м°р » Wz2 Используя эти уравнения, можно получить максимальные растягивающие и сжимающие напряжения, обусловленные изгибом, если известно отношение модуля упругости. Приведем формулу (11.53) в несколько ином виде. По формуле(11.50)、 ^2 _ _ _ г П Введя это соотношение в Формулу (11.53)、 Регистрация Е Р з м Р » bh2(■+(11.54) АГВ °C W~bh2 (*+o-(11.55)) В таком виде формула удобна для расчета напряжений, когда относительная деформация измеряется в крайних волокнах балки с помощью тензометрического датчика.
Смотрите также:
| Касательные напряжения при изгибе балок тонкостенного профиля. центр изгиба | Сложный и косой изгиб |
| Основы расчета балок на упругом основании | Изгиб с растяжением (сжатием) |

