Оглавление:




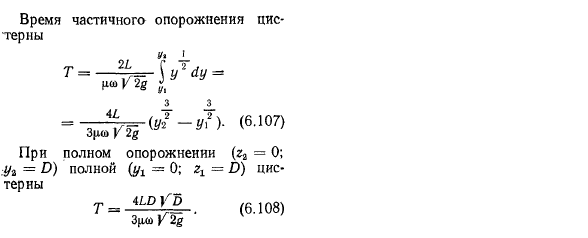

Истечение жидкости при переменном напоре
Истечение жидкости при переменном напоре. Рассмотрим наиболее распространенную проблему-отток жидкости при переменном давлении из сосуда любой формы поперечного сечения (Фf sot!).И наличие переменного потока жидкости в контейнере (UV 0) (рис.6.16). В общем случае непрерывное уравнение движения (уравнение равновесия жидкости) для этой задачи можно описать следующим образом: No. pr = Нет. Ист + ГОСТ. (6.62) За бесконечно короткий промежуток времени<11 в сосуд поступило определенное количество жидкости (приток). Шлр = уд.1. (6.63).
В этот же период из емкости вытекает определенное количество жидкости (объем стока) shNST = он,(6.64) Где 0-скорость потока. Разница между этими объемами составит оставшуюся сумму Ш0 «^Шпр-Шк». (6.65)) Объем остатка можно представить как произведение площади поперечного сечения емкости J и приращения уровня жидкости в ней (то есть приращения давления) dg. Где r-переменное давление жидкости в контейнере. И затем… 。 。 № 0 ″ =Шг. (6.66) Подставляя результаты, полученные в (6.65), мы получаем дифференциальные уравнения неразрывности для движения в случае жидкости, которая присутствует для течения при переменном давлении. η= y <11-Cl1. (6.67).
Расчетный напор при истечении под уровень представляет собой разность гидростатических напоров по обе стороны стенки, т.е. скорость и расход не зависят от высоты расположения отверстия. Людмила Фирмаль
- А потом это продолжается. ^ =(6-68) У нас есть главная зависимость Подача жидкости от отверстий и сопл должных к переменному давлению и присутсвию influx. To действительно, используя вышеприведенные зависимости, нужно знать, как изменяется скорость течения притока и характер изменения площади поперечного сечения сосуда по его высоте с течением времени. Если площадь отверстия равна ω, а расход притока равен y = const, то давление, при котором расход потока равен постоянному расходу притока.
Если фактическое давление в контейнере в любой точке равно r, то расход при 2 <Н равен C)■ < y, и уровень жидкости в контейнере увеличивается до тех пор, пока он не станет равен H\; 2>Н, а расход q уменьшается до тех пор, пока жидкость в контейнере не станет равна N. Определите расход при определенном давлении в конкретный момент по следующей формуле д = = РЮО!/2§ 2, (6.70) Это верно в случае оттока при постоянном давлении, и если подставить уравнение y и C в (6.68) и интегрировать его, то можно заметить время T, когда уровень жидкости в сосуде изменяется от 2]до 2a. распространенные случаи утечки жидкости при наличии 116.
- Постоянный приток Т = {2Я… г. ГСП. ’gmt РГГМУ здоровья-к?’ (6.71)) При изменении давления, коэффициента сжатия струи е и частично коэффициента скорости cf. So, в общем случае коэффициент потока равен p = /(g).Однако, когда жидкость с низкой вязкостью, такая как вода, истекает, коэффициент расхода изменяется незначительно. Учитывая, что в некоторых расчетах пределы изменения давления обычно не столь велики, в таблице фактически приведены средние экспериментальные значения коэффициента расхода с достаточной точностью, поэтому можно считать Р = const.
Затем время, в течение которого уровень жидкости в контейнере изменяется от g1 до g2 Т. 1. РШ П2§ 0 < Ар ООН-у-г (6.72) Обратите внимание, что если сильно вязкая жидкость вытекает, изменение p не может быть проигнорировано. Для того, чтобы фактически использовать зависимости (6.71) и (6.72), необходимо знать= = /<sup class=»reg»>®</sup>. Рассмотрим частный случай истечения жидкости при постоянном расходе из цилиндрического или призматического сосуда с вертикальной осью, когда площадь поперечного сечения сосуда равна= = sop. (Рис. 6.17).
Ввести новые переменные для интеграции (6.72) г = ООН-ви(6.73) И затем… 4 года—2-g=, (6.74) Или Ю. Г.-Г Г 2 ю. (6.75) Но -гг-р = г-ООН! (6.76) Для этого АГ = 2 (у-УН) Лу. (6.77)) Пределы интеграции с новыми параметрами г ^ ООН-Ыб(6-78) у = УН-Уч. (6.79) Замените переменную на следующую y * _ т. 20. да./ к-\ г-ООН \ ПУ \ yy2g(6.81) РШ У2.§ Мы можем заменить пределы интеграции、 Т =% =■[ООН-УГ2-ООН + РШ У2.§ + UG1-UN 1p (UN-U72)+ + UN1n (ООН〜обновление 71)\. (6 82) 11? Наконец, время, в течение которого уровень жидкости в сосуде изменяется от начального давления g1 до конечного g2 Т. 20 ц) в Уу-у Г2 + + г н Г-н-г г±УН— г Г2 (6.83).
Таким образом, время полного опорожнения резервуара в два раза больше времени истечения того же объема жидкости при постоянном напоре. Людмила Фирмаль
- Это уравнение равно = = const!, П= сопи! Он может быть применен к: y = заморозить! Причем это касается как снижения, так и повышения уровня жидкости в контейнере. На практике часто возникают проблемы, связанные с эвакуацией кровеносных сосудов. Решая их, отметим, что пустота может быть только при отсутствии притока, то есть при 7 = 0, а следовательно, только при H = 0. Следовательно, частичное время опорожнения призматического или цилиндрического сосуда с вертикальной осью (6,80) H = 0 Т =21Γ (в ^ вю), (6.84).
И время до полного опустошения(ha = 0) Жидкость и?! он течет в 2 раза быстрее, чем при его полном опорожнении с изменением уровня (давления) от yy до 0. Рассмотрим еще один очень важный для практики случай, когда отток переменного давления происходит не в атмосфере, а происходит из одного квадратного цилиндра (цилиндра с вертикальной осью) в другой, то есть под переменным уровнем. В этом случае (рис. 6.18) в течение времени нахождения ка в сосуде а уровень жидкости в сосуде в уменьшается на величину а и увеличивается на величину n2.As в результате изменения уровня жидкости в этих сосудах за рассматриваемый период времени.
Смотрите также:
Возможно эти страницы вам будут полезны:

