Оглавление:






Истечение газа из резервуара неограниченной емкости
- Представьте, что газ течет через коническое сопло в резервуаре, который достаточно велик по размеру (рис.10.4). Параметры газа в баке показаны в p, 0c 7. Значения этих параметров из-за размера резервуара не должны меняться в течение времени. Предполагается, что начальная скорость газа в баке равна нулю (ω,= 0). Температура, удельный объем, давление и скорость на выходе (срезе) сопла обозначаются T, V, p, it. Давление внешней среды, в которой происходит отток обозначается РГ. Так называемый расчетный режим течения p = p, то есть давление на выходе из сопла должно быть равно давлению окружающей среды во время течения.
Если в рассматриваемом случае отток газа является обратимым и адиабатическим, то из формул (10.18) и (10.21) Когда газ вытекает из резервуара, получается максимальный расход газа. Его величина определяется давлением на сопле outlet. To определите максимальный расход, получите производную 1-го порядка выражения в скобках и установите ее в ноль Из последнего выражения Отношение давления p / p]называется критическим и обозначается 0cr. Соответствует критическому давлению выхода сопла Критический коэффициент давления зависит только от физических свойств газа, точнее его адиабатического индекса. k = 1.4 p » p = 0.528 для 2-атомного газа.
В каждой аэродинамической трубе существует турбулентность, создаваемая в потоке воздуха воздуходувкой. Людмила Фирмаль
Подставляя максимальный расход для Формулы 2-го потока, можно увидеть следующее: 6Т, х = Заключите выражение в скобки Преобразования, находим в. Величина максимального расхода соответствует критической скорости aivr. Критическая скорость возникает только тогда, когда перепад давления равен следующему Др = Р₁-р₁ф=Р₁ (1-РКР).
Подставляя ПЦР значение формулы (10.23) в уравнение расхода, получаем: (10.25)) Поэтому критическая скорость конкретного рабочего тела зависит от величины параметров начального состояния. Критический расход является максимальным Максимальная скорость истечения газа через сходящееся сопло при определенном начальном состоянии газа. Критическая скорость равна Поток оболочки равен скорости звука, то есть локальной скорости звука, в выходном сечении сопла. Отношения критического раздела Затем подставьте эти значения в выражение (10.25), чтобы получить их после преобразования ) ’ = а.
Скорость звука — это скорость распространения мельчайших возмущений в сплошной среде, которая зависит от упругих свойств и плотности среды. Звуковые волны практически не обмениваются теплом между частью, через которую проходят звуковые волны, и остальной частью газа, так что состояние изменяется без подачи или удаления тепла в адиабатическом состоянии. Из-за небольших изменений в состоянии газа в волнах разрежения и сжатия, действие внутреннего трения очень мало, а распространение звука reversible. It можно считать а). Скорость распространения звука определяется по формуле круга- Где P-давление среды, Н! m * \ p-плотность среды, кг / м*.
- Значения скорости звука различных газов приведены в таблице. 10-1. Таблица 10-1 скорость звука в Газе при 15°C ….. г.. — л. Водород…. 1.66 1000 воздух сухой. 1.4 347 Кислород. 。 1 * 4 1320 углекислый газ. 。 1.4 342 323 1.31 273 С Р = 1 / о Затем_ а =] /Кри. Для идеального газа, pV = IT on-UKNT. так как a = V-kNT, каждая секция сопла должна иметь свою собственную локальную скорость звука, которая определяется значениями P и o в этом случае section.
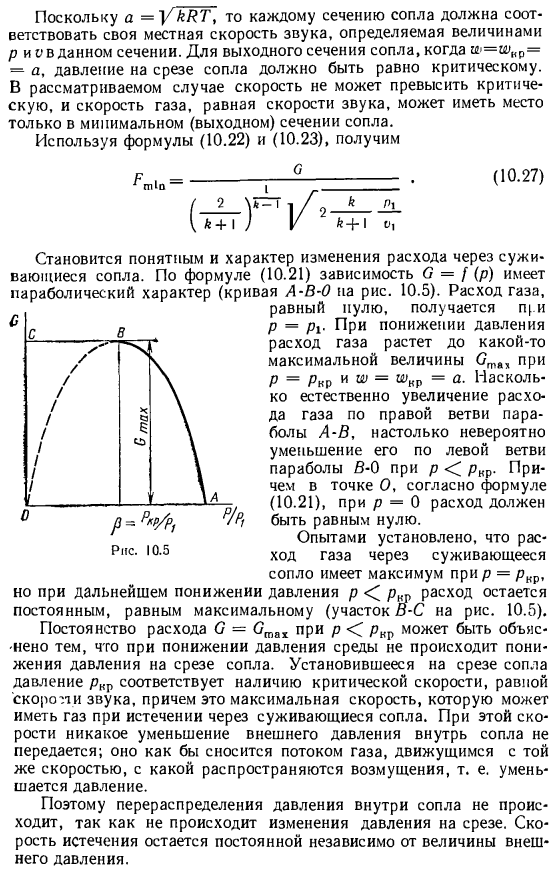
In вВыходное сечение сопла, если a> =И1вр = = a, то давление на выходе из сопла должно быть равно критическому. Если рассматриваемая скорость не может превышать критической скорости, то и скорость газа, равная скорости звука, возникает только в минимальном (выходном) сечении сопла. Используйте выражения (10.22) и (10.23), чтобы получить: Становится понятным и характер изменения расхода через сопло. Согласно формуле(10.21), зависимость O = [(p) обладает свойством параболы (кривая n» n -, n o — «» …Рисунок A-B-0 10.5). при o = P1 мы получаем газовый поток, равный пуле. При падении давления поток газа увеличивается до максимальных значений St> to = / > bp и a> = svr = A.
Первая часть струйки дыма представляет собой ламинарную форму потока, а вторая — турбулентную. Людмила Фирмаль
Насколько естественным является увеличение потока газа вдоль правой ветви параболы AB, настолько уменьшение потока газа вдоль левой ветви параболы B-0 при p , дополнение, точка O. In в соответствии с формулой (10.21), при Р = 0 расход должен быть равен нулю. Эксперименты показали, что поток газа через сужающее сопло максимизируется при p = pbp, но при дальнейшем понижении давления p расход остается постоянным, равным максимуму(BC На рис.10.5).Инвариантность потока O = p можно объяснить тем, что давление на выходе из сопла не уменьшается, даже если давление среды уменьшается. Давление pkr, установленное на выходе из сопла, соответствует наличию критической скорости, равной скорости звука.
Это максимальная скорость, которую газ может иметь при прохождении через сходящийся nozzle. At этот тариф, падение в внешнем давлении не передан к nozzle. It это как если бы возмущение несло газовый поток, движущийся с той же скоростью, с какой он распространяется. То есть давление будет снижаться. Поэтому перераспределения давления внутри сопла не происходит, так как не происходит изменения давления на срезе. Расход остается постоянным независимо от величины внешнего давления.
Теперь давайте проанализируем изменение состояния газа в сопле, когда газ течет от входа к выходу. Газ идеален, то есть в соответствии с уравнением Клапейрона, и его течение предполагается изоэнтропийным. Уравнение изоэнтропийного течения газа в сопле может быть записано в дифференциальной форме. Радиоуправляемый) = Со Форма после дифференциации &&1> 4-ich1P = Oo. Если разделить обе части на rchi、 Из Формулы (10.13) (10.30) Уравнение (10.28)、 — Скорость звука Замена значения В этом уравнении、 Для того чтобы понизить скорость звука, сопло Жизнь в направлении движения газа. Если скорость потока больше скорости звука a ’- u / ’ O, сопло должно расширяться в направлении газа.
Смотрите также:
| Располагаемая работа газа в потоке | Расширяющиеся сопла |
| Скорость истечения и расход газа | Истечение при наличии трения |

