Задача №40.
Исследовать условия равновесия тяжелой материальной точки, на которую наложены связи
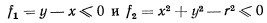
(здесь предполагается, что ось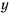 
направлена вертикально вверх, а ось 
— горизонтальна).
Решение:
Уравнение равновесия получает вид
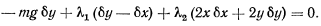
Приравнивая нулю коэффициенты пр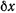и 
и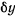 
, получим
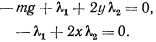
Присоединяя к этим уравнениям еще уравнения связи, будем иметь
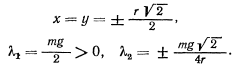
Но так как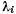 
в положении равновесия должны быть все отрицательными, мы приходим к заключению, что материальная точка не может находиться в равновесии при действии обеих связей.
Предположим теперь, что одна из связей, скажем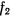 
, освобождена и на точку в положении равновесия действует только одна связь 
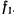. Получаемые при этих условиях уравнения равновесия
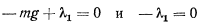
оказываются противоречивыми, следовательно, такого положения равновесия не существует.
Остается рассмотреть случай, когда освобожденной оказывается связь 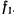. Уравнения равновесия тогда получают вид
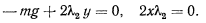
Эти уравнения имеют решение
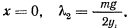
Отрицательное значение для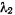 
получается только в том случае, когда 
, поэтому будем иметь для положения равновесия следующие значения
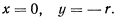
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
