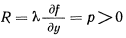Задача №39.
Исследовать условия равновесия материальной точки, находящейся под действием силы тяжести, на гладкой горизонтальной плоскости.
Решение:
Горизонтальная плоскость может рассматриваться как односторонняя связь, которая допускает отрыв точки от плоскости вверх. Поэтому, если ось 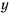 направить вертикально вверх, условие связи запишется в виде
направить вертикально вверх, условие связи запишется в виде
а основное уравнение равновесия
Отсюда имеем 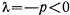 и, следовательно, равновесие точки не зависит от ее положения на плоскости.
и, следовательно, равновесие точки не зависит от ее положения на плоскости.
Метод Лагранжа дает возможность определять и реакции связей. В рассматриваемом случае реакция будет равна
и, следовательно, направлена вертикально вверх.
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
| Задача №37. Рассмотрим задачу о равновесии системы, состоящей из шарнирного четырехзвенника , к шарниру которого приложена вертикальная сила , а звено жестко связано с диском, центр которого находится в точке . К диску в точке по касательной приложена горизонтальная сила . Размеры в положении равновесия системы указаны на чертеже. Пренебрегая весом стержней и диска, а также трением в шарнирах, определить соотношение между величинами и в положении равновесия, указанном на чертеже (рис. 30). |
| Задача №38. Пусть имеется однородный стержень длины , опирающийся одним из своих концов на криволинейную направляющую, имеющую форму окружности радиуса (см. рис.31). Пусть этот стержень касается некоторой точки окружности, находящейся в конце горизонтального диаметра. Определить, пренебрегая трением, положение равновесия стержня и исследовать его на устойчивость. |
| Задача №40. Исследовать условия равновесия тяжелой материальной точки, на которую наложены связи (здесь предполагается, что ось направлена вертикально вверх, а ось — горизонтальна). |
| Задача №41. Материальная точка с массой m находится в равновесии внутри трехосного эллипсоида с полуосями и . На точку действуют силы: сила тяжести, параллельная оси , и сила отталкивания от оси , пропорциональная расстоянию точки от этой оси. Найти положение равновесия точки. |

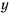 направить вертикально вверх, условие связи запишется в виде
направить вертикально вверх, условие связи запишется в виде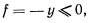
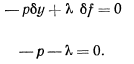
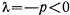 и, следовательно, равновесие точки не зависит от ее положения на плоскости.
и, следовательно, равновесие точки не зависит от ее положения на плоскости.