Оглавление:






Исследование вынужденных колебаний
- Амплитуда и фазовый сдвиг вынужденных колебаний A и e за счет (46) не зависят от начальной фазы 8 возмущения. Например, при их расчете можно предположить, что 8 = tr / 2 + e. Если возмущение является константой, равной амплитуде H, то правая часть уравнения (44) также будет постоянной, и в качестве конкретного решения неоднородного уравнения q2 принимают постоянное значение статического смещения q2 = h / k2 Я могу Проверка подтверждает, что это значение q2 удовлетворяет уравнению (44).
Рассматривая (46) как частный случай, соответствующий p = 0 и 8 = — + e, вычисление q2 из (45) согласуется с 2 = (Я) /, = Po = A0 = h / k2 вы. Статическое смещение. Поэтому A0 ~ h / k2 можно рассматривать как «амплитуду» вынужденной вибрации под действием постоянной возмущающей силы. Сопоставьте наибольшее значение гармонической возмущающей силы с модулем. Значение A / Ao называется коэффициентом динамичности. Динамический коэффициент характеризует относительную величину амплитуды вынужденных колебаний.
Возможные перемещения в точке или в точках линии соприкосновения равны нулю в каждый момент времени, так как равны нулю скорости в точках соприкосновения, как и для закрепленных точек. Людмила Фирмаль
Другими словами, он показывает, во сколько раз амплитуда вынужденных колебаний под действием гармонической возмущающей силы отличается от статического смещения. Это вызывает постоянную возмущающую силу с величиной, равной максимальному значению гармонической силы. Это исследование показывает, что динамический коэффициент может быть значительно больше 1, если сопротивление достаточно мало. Изучите динамический коэффициент. Найдите, когда взяты максимальные и минимальные значения, когда они имеют тенденцию быть равными нулю и так далее.
Учитывая значения A и Ao, после преобразования: Вот некоторые обозначения. z = p / k — коэффициент расстройки или относительная частота возмущающей силы. h = n / k — коэффициент относительного демпфирования. Динамический коэффициент зависит от параметров z и b. Изучите изменение в ответ на изменение z для фиксированного значения b. Из (47) динамический коэффициент стремится к нулю при z-> oo и относительном коэффициенте ослабления b. В результате, если коэффициент k очень мал по сравнению с p (z = p / k- * co), амплитуда вынужденной вибрации A стремится к нулю.
В этом случае эффекты высокочастотных помех не распознаются вибрационной системой и не нарушают естественный режим вибрации, который затухает под воздействием сопротивления линейной системы. Это свойство вынужденной вибрации фактически широко используется при транспортировке товаров, которые не могут противостоять ударам. На транспортном транспортном средстве нагрузка подвешена такой пружиной, поэтому частота естественной вибрации мала по сравнению с частотой силы возмущения (удар от рельсового сочленения автомобиля, разгрузка автомобильной дороги).
Воздействие от регулярности, вибрации самолета от работающего двигателя и т. Д.). ) Использование пружин в разных видах транспорта основано на одинаковых характеристиках вынужденной вибрации. Для дальнейшего исследования динамических коэффициентов введем функцию f (z) = (l-z2) 2 + 4b2z2. Это зависит от z и параметра b. тогда ■ Очевидно, что когда / (z) достигает максимального значения, A / Ao становится минимальным значением, и наоборот.
Вычислить производную по z, чтобы определить экстремальное значение / (z). / ‘(Z) = -4z (l-z2) + 8Z> 2z = -4z (l-2Z> 2-z2); / «(z) = -4z (l-z2) + 8z2 + 8Z> 2 = 8z2-4 (1-2b2-z2). Функция / (z) достигает предельного значения значения z, где f ‘(z) = 0. Получить два значения из этого условия для z. Относительная частота является положительным значением и равна нулю для постоянной возмущающей силы, поэтому 1-2L2> 0. Следовательно, L 0, поэтому f (z) имеет минимальное значение, а динамический коэффициент имеет максимальное значение.
- Для значения b для I-2 /> 2 = 0 (/> = ^ / 2/2) Zj = z2 = 0 и f (z) = 0. В дополнительных исследованиях третьей и четвертой производных f (z) в этом случае минимальна при z = 0. Динамический коэффициент имеет максимум, а f (z) не имеет другого экстремального значения. Если 1–2 /> 2 <0, z2 чисто мнимый. Это можно интерпретировать как отсутствие другого значения z, кроме z = 0. Когда z = 0, / (z) достигает крайнего значения. Минимальное значение достигается при z = 0 / (z), а коэффициент динамичности достигает максимального значения. При увеличении z динамический коэффициент 1-2h2 ^ 0 монотонно уменьшается от максимального значения z = 0 до нуля при z-> oo.
Результаты исследования динамического коэффициента представлены в виде так называемой резонансной кривой или зависимости A / Ao от z для различных значений амплитудно-частотных характеристик системы (рис. 124, а), относительного коэффициента демпфирования b вы. Если /> = 0, использовались результаты, полученные без сопротивления. Это исследование может сделать дополнительные выводы о влиянии линейного сопротивления на вынужденную вибрацию.
Силами реакций связей в этом случае являются внутренние силы, для которых было доказано, что сумма элементарных работ этих сил на любых элементарных перемещениях точек тела равна нулю. Людмила Фирмаль
Следовательно, максимальное значение коэффициента динамичности и, следовательно, максимальное значение амплитуды вынужденного колебания не является резонансным, когда r = 1 (p = A), но возникает при значении z = z2 = -2b2, которое меньше 1. Чтобы получить значение Максимальная амплитуда Am должна быть заменена в уравнении (47) на z2 =, / 1-2b2, что соответствует критическому значению круговой частоты силы возмущения Для h меньше единицы, ^ max «^ o / (2 ) — Амплитуда вынужденной вибрации при резонансе Лр „получается из (47) при r = 1. yari = l / (2lL) = l0 / (a ») 2-P2) 2 + 4 ”2P2 s / (l-z2) 2 + 4b1z2.
Для безразмерных (относительных) амплитуд, которые являются аналогами коэффициентов динамизма, A / h0 = z2 / y / (\ -z2) 2 + 4b2z2. Граф A / h0 облегчается введением вспомогательной переменной zt = -. Зависимость A / h0 от zt согласуется с зависимостью A / Ao от zt. График уже построен (рис. 124, а). Чтобы перейти от z к z в точке A / h0, необходимо учитывать, что z, = cc становится z = 0, z, = 0 в z-oo и z, = 1 в z = 1. На рисунке 124.6 показана амплитудно-частотная характеристика системы в этом случае. Величина h0 больше не является статическим смещением Ao. Изучите влияние линейного сопротивления на сдвиг фаз. Согласно (46) tGE = 2np / (k2-p2) = 2bz / (\ -z2), 0 <ε <1. (46 ‘) Тангенс сдвига фазы e выражается в виде простой зависимости от z.
Используя монотонность изменения тангенса как функцию изменения аргумента, легко построить зависимость £ от z от различных фиксированных значений b. Если сопротивления нет, e = 0, если z l, подготовьте необходимые данные. Из (46 ‘), если z = 0 tan £ = O, c = 0 получается с учетом значения, когда сопротивление отсутствует (e изменяется монотонно и непрерывно в соответствии с b). Для z = l, tge = oo, поэтому e = l / 2, а также отсутствие сопротивления. Для z- »oo, tgE- * 0 это -». Это соответствует. Учитывая монотонность касательной, получается результат e. z = 0, £ = 0; 0 <z <l, 0 <e <l / 2; z = 1. е = 1/2; 1 <z <oo, l / 2 <e <1r.
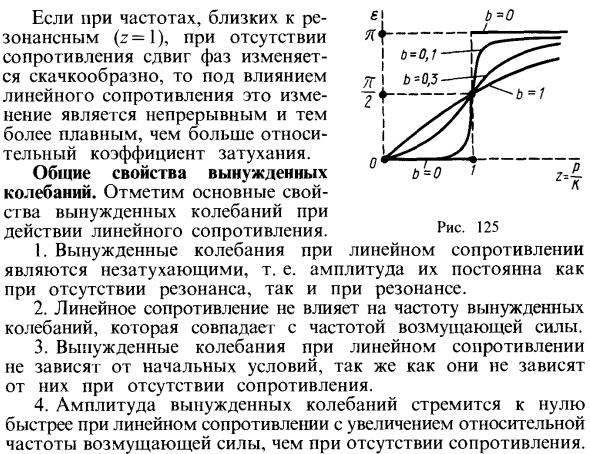
С помощью этих данных вы можете построить график фазового сдвига (частотно-фазовые характеристики системы) как функцию относительной частоты возмущающей силы для фиксированного значения относительного коэффициента демпфирования (Рисунок 125). Поскольку тангенс фазового сдвига не зависит от h, частотно-фазовые характеристики системы не зависят от метода гармонического возбуждения. То же самое для динамических и кинематических возбуждений. Исследования фазового сдвига показывают, что фазовый сдвиг в резонансе не зависит от линейного сопротивления. равно л / 2.
Линейное сопротивление На частотах, близких к резонансным (z = 1), в отсутствие сопротивления фазовый сдвиг изменяется ступенчато, и под воздействием линейного сопротивления это изменение является непрерывным и чем плавнее, тем больше относительный коэффициент демпфирования. , Общие характеристики вынужденной вибрации. Обратите внимание на основные характеристики вынужденной вибрации под действием линейного сопротивления. Принудительная вибрация в 1.
Другими словами, амплитуда постоянна как при отсутствии резонанса, так и при резонансе. 2. Линейное сопротивление не влияет на частоту вынужденных колебаний. Это согласуется с частотой возмущающей силы. 3. Вынужденная вибрация линейного сопротивления не зависит от начальных условий, так как она не зависит от отсутствия сопротивления. 4. Амплитуда вынужденной вибрации имеет тенденцию быть быстрее в нуле с линейным сопротивлением, поскольку относительная частота возмущающей силы увеличивается, чем без сопротивления.
Смотрите также:
Задачи по теоретической механике
| Дифференциальное уравнение вынужденных колебаний и его интегрирование | Основы виброзащиты |
| Основные свойства вынужденных колебаний | Математический и физический маятники |

