Оглавление:









Исследование уравнений сохранения методами теории подобия и анализа размерностей. Задачи
- Высотная зависимость атмосферного давления. Р. расположенный на южном берегу озера Верхнее (183,6 и ВАД) на реке тоннаж (1stv, Мичиган, США), портативный барометр показывает давление 750 мм рт. ст. Искусство. Используя уравнение движения, мы оцениваем барометрическое давление правительственного пика (616,6 над уровнем моря) вблизи поки. 9.81 м / С⁸; при расчете изменения этой величины в height необходимо игнорировать. Ответ: 712 мм рт. Искусство. 3-2.
Определение вязкости с помощью вискозиметра Куатта-Гатчека или вискозиметра Макмайкла. Измерьте вязкость раствора сахарозы в вискозе Pi^ ⁶ ⁶Luetta-Gatchek. In в неподвижных внутренних цилиндрах устройства имеются концентрические цилиндры диаметром 4,5 см, эффективная длина которых равна Внешний цилиндр вращается под действием известного крутящего момента, а вязкость исследуемой жидкости определяется путем измерения угловой скорости вращения, установленной в ходе эксперимента. Вязкость раствора сахарозы составляет 60 мас.%.%При 20°C составляет около 57 cP, а плотность-около 1,28 г-см.
Последние могут быть снова выражены условно в безразмерном виде: с индексом 0, обозначающим условия на достаточном расстоянии от цилиндра. Людмила Фирмаль
В результате предварительных испытаний выясняется, что важен «конечный эффект«.Поэтому было решено откалибровать вискозиметр / раствор сахарозы, который был протестирован путем проведения измерений с несколькими известными растворами с почти одинаковой вязкостью. Если надежное измерение крутящего момента возможно в течение 100 дней-см, а угловая скорость найдена с точностью 0,5%, то во время калибровки определяют крутящий момент, добавляемый к внешнему цилиндру. Какова требуемая угловая скорость? 3-3.Применение уравнения Навье-Стокса в постановке простой задачи.
Используйте уравнение Навье — Стокса (p = const1), чтобы получить дифференциальное уравнение распределения скорости.1) когда изотермическая пленка жидкости вытекает (см. раздел 2.2). 2) 2-фазный поток в горизонтальном зазоре(см. раздел 2.5). 3) осевое течение в кольцевом зазоре с подвижной границей (см. задачу 2-7). 3-4.Распределение скорости вискозиметра Штормера. Этот вискозиметр состоит из 2 концентрических цилиндров, внутренний цилиндр вращается, внешний цилиндр остается неподвижным.
Вязкость определяют путем измерения скорости вращения внутреннего цилиндра под действием известного крутящего момента. Устройство аналогично вискозиметру Couette-Gat-check, который рассматривался в разделе 3.5. Получить формулу распределения скорости для данного типа устройства^ Характеристики жидкости. ^ r из определяющего уравнения движения、 Он построен на основе динамической вязкости p (уравнение несжимаемой жидкости (P-d), стр. 871.Следуйте уравнению неразрывности несжимаемой жидкости (v-c)= 0.Вы должны использовать это отношение. а) упростить уравнение (Ya) tx(см. стр. 90) м.= = = =- 2П -^- От скорости 3-6. 2. распределение скорости между двумя вращающимися цилиндрами.
Найти ЕС между 2 коаксиальными цилиндрами, имеющими радиус и и xЯ и вращающимися с угловой скоростью о и соответственно соответственно. Предположим, что пространство между цилиндрами заполнено несжимаемой изотермической жидкостью, которая движется слоями. Элементы объема, движущегося вместе с жидкостью, то есть уравнения (3.17) и (3.19), эквивалентны. 3-8.Уравнение неразрывности цилиндрических координат а) выводит уравнение неразрывности цилиндрических координат и создает массовый баланс элементов фиксированного объема gDGDYDg. б) получить уравнение неразрывности в координатах цилиндра и угля путем замены координат re-variable. In вывод, следующее соотношение приемлемо без доказательств.
Доказать справедливость данного выражения 3-9; радиальная система сепаратора утечки состоит из следующего: U расхода потока в системе между радиусом r₂ (см. Рисунок 3-7). а) напишите УР. Активный——-. В случае пунктов «в», «с». Между 2 параллельными дисками. Часть SMA состоит из 2 круговых дисков, во время которых происходит радиальное: перепад давления Dr И поток является стабильным ламинарным потоком. Рассматривается только область G1 3 в r r мы предполагаем, что поток происходит радиально (ev = 0).
Как использовать уравнение неразрывности、 Ю вода ЛР | Н РЧ (3.126) Где p = hcr-функция только координаты 2, но почему a>не зависит от r? в) если не игнорировать нелинейный член (то есть член, содержащий pa), то можно видеть, что выражение (3.126) не имеет решения. Отказ от этого термина соответствует предположению о «ползучем потоке», сделанному в разделе 2. при выводе закона Стокса, обтекающего сферу.
- Если нелинейный член опущен, уравнение движения может быть интегрировано. Скорость (3.127) (3.128) (3.129) 4пб 3I1n ^- (Схема) распределение давления p (g) Действие 。Нулевой объем Тзд = т » х (3.130) * * Местных * также в системе координат.) ’3-11.Применение теории подобия и размерного анализа Метод формы. При изучении поведения неньютоновских жидкостей И анализ «MeT⁰D°B ^» будет рассмотрен уравнение движения. Покажи мне. Т М1 Н-1М(Р + Дм) — Оствальда-Вейля[Формула^ Х⁾ — О ^(xvLx). — Она жесткая, АОЛ.- Равный рекорд Нет 1Ф°Р Т «’» Ха Замечание. П Тензор t symmetry. In прямоугольное УТИ (рис. 3-9), 4 тангенса нанора I, перпендикулярные оси, образуют пару сил.
Написание выражений уязвимости и действий ech в результате Размер элемента, чтобы стремиться (Отмечать Другие ортогоны Цифры 3-9.Объемный элемент, размер Г^ 1; 1×3131⁾ Если Дю да, Каса-и 3 показаны Стресс, действующий на речь. Держал В плоскости плоскости, вертикальный анализ формально был коронной осью r. момент силы вычисляется. Однако в этом случае она прослеживается относительно проходящей оси. Обратите внимание, что точка разреза не Ньютона равна 0.
Рассматривая снова поток, обтекающий круглый цилиндр, нам придется иметь дело не только с полями скорости, давления и температуры, но также с полями плотности, вязкости и теплопроводности. Людмила Фирмаль
Будучи физическим, он не точно описывает поведение реальной жидкости. 3-12.Радиальный поток между концентрическими сферами. Рассмотрим изотермический поток несжимаемой жидкости, которая движется радиально между двумя концентрическими пористыми оболочками в форме сферы (рис.3-10).Предположим, что поток является устойчивым ламинарным потоком, без учета конечного эффекта, а также отметим, что здесь скорость твердой поверхности равна нулю r31>,=φ(3.132) Где F-константа. б) используя уравнения движения, выясните, что распределение давления таких систем описывается следующим соотношением: Тринадцать г- || = пр1 (3.134) Поиск с помощью c) отображение по формуле (1U-d) на стр.
Радиальное распределение давления P = * «» г)в связи с этим опишите формулы t, tvv и tvt Задача. Какое из перечисленных нормальных напряжений является сжимаемостью? Что означает ваш физический^ Ответ? Я Л » ’Х e) сжимаемый и & /равный Напряжение растяжения, ОК — / ’ л. \ ___ / / Влияет на внутренний/ / / V」 И каждый из них、// // \\ «Между» Химическая несжимаемая жидкость, 2-H / teadD~~) » | { Зажатый между 2 пористыми cy и \ \ 7?- м а) уравнение K /(yU heg = f (3.137) рисунок s_y.
Радиальный поток между Концентрическая пористая сфера, где w-постоянная. Б) упростите уравнение движения, чтобы получить следующее уравнение распределения давления в зависимости от Р: «» » > ^ г — 5г -«’» > c) найти выражение, интегрируя выражение LR / Lg из точки » b» Р-рь = | р»> | g_ya [1-(Ас] (3.140) 3-14. 2. ползучий поток между двумя концентрическими сферами. Через пространство между двумя концентрическими сферами протекает высоковязкая жидкость (рис.3-11).Представляет скорость потока как функцию разности давлений, приложенных к системе. Не рассматривая конечный эффект, установите 1>₉= 1> in(r 0) и V,=Л= 0. а) используйте уравнение неразрывности, чтобы указать, что e, yn 0 = u.
Где u (0-функция в r, которую необходимо определить. Б) записать выражение 0-й составляющей уравнения движения примитивно малым настолько, чтобы все члены в левой части этого уравнения могли быть ignored.
Также показано, что это выражение сводится к следующему виду B-часть d) Показать、 в) разделить предыдущие отношения d) используя результаты, вы можете найти ваше потребление Зло「」 3-15.Выражение компонента напряжений по компоненте расхода и физико-химическим свойствам неньютоновской жидкости. а) проверить правильность формулы (3.77) на основе формулы (2.48). D * b) используя формулу (3.79)、 Е11 -、 Это соответствует формуле (3.88). c)для неньютоновских жидкостей, подчиняющихся закону экспоненты, используйте результат в пункте «b»для получения аналога уравнения Райнера- 3-16.Вывод уравнения движения Неподвижные элементы объема C имеют конечный объем и поверхность 5C.
Опишите 2-й закон движения Ньютона для всего управляющего объема в соответствующем уравнении(3.10).Поскольку условия внутри этого объема нельзя считать однородными, необходимо интегрировать скорость накопления импульса и объемную силу на объеме Ve, а также конвективную силу на поверхности 5c. 3-11.Теорема ползучести о дивергенции преобразует Интеграл между 2 неподвижными поверхностями на поверхности в Интеграл объема и концентрических сфер. Окончательное выражение может быть уменьшено, скажем 3-17.Выведение распределения скоростей вискозиметра с вращающимся конусом и неподвижной пластиной путем упрощения уравнений движения.
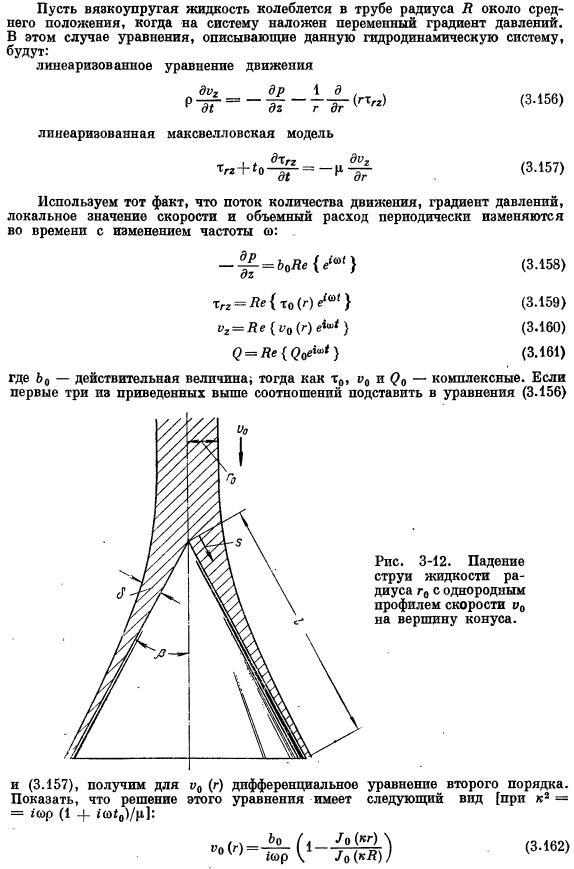
Получить B — (r, 6) формулу (3.69) иным способом, чем использовалось ранее. *В русской литературе эту теорему обычно называют теоремой Гаусса-острограцкого. — Отмечать. Эд. (20, 21], здесь U = (9), указывая на возможный нормальный дифференциал В следующих граничных условиях: Затем была получена несжимаемая жидкость [4? -[о•(V » > 1] +Ууо] = — UR + iu2o + P? 3-19.Регулярный (3.162) Расширить функции Бесселя (3.163) Линия, которая держит все Используя уравнение (3.161) и определение k, для o> 1>€1, я использую br (3.165) Обязательно интерпретируйте результаты физически. 3-20.Капля жидкости плевок cones.
Смотрите также:

