Оглавление:







Исследование уравнений сохранения методами теории подобия и анализа размерностей
- После получения уравнений сохранения неизотермической системы и демонстрации того, как решить проблему теплопередачи с помощью этих уравнений, рекомендуется легко проанализировать размеры этих уравнений. Рассмотрим его как введение к главе 13. Для простоты, следующие расчеты относятся к системам с определенными физическими характеристиками.
Такая система может быть описана следующими одновременными уравнениями, как описано выше: непрерывные уравнения (ООН)= 0 (10.105) Уравнение движения Переменный ток+ (- ВП + Р?(Вынужденная конвекция) I — £r£(Г-Го) (естественная конвекция) (10.106) Уравнение энергосбережения Серия — ^ -^ АР + ПФО (10.107) Отметим, что для унифицированного описания процесса форсированного форсирования и естественной конвекции уравнение(10.106) представлено в виде уравнения с «источником импульса».Однако, поскольку удобнее характеризовать эти 2 типа систем с различными безразмерными переменными, размерный анализ систем с принудительной и естественной конвекцией проводился раздельно.
Его результаты для чисел (Прандтля 0,5—10 можно выразить формулой В большом количестве работ расчеты распространяли на газы с переменными свойствами. Людмила Фирмаль
Температура, указанная в Формуле (10.106), принимается равной температуре окружающей среды. Для систем с принудительной конвекцией безразмерные переменные определяются как: безразмерная скорость (10.108) Безразмерное давление Безразмерное время Безразмерная температура Безразмерные координаты (10.109) (10.110) (10.111) (10.112) Где величины V, D и (1 \-Go) представляют характеристическую скорость, размер и разность температур системы, respectively. In переменная (10.108)-(10.112), уравнение сохранения принимает вид: (10.113) (10.114) (10.115) (Г * -Т *)= 0 И » «* _ в * ПФТ ⁺ *’ » Где Фр-диссипативная функция, описываемая безразмерными переменными V*, x*, y * u*.
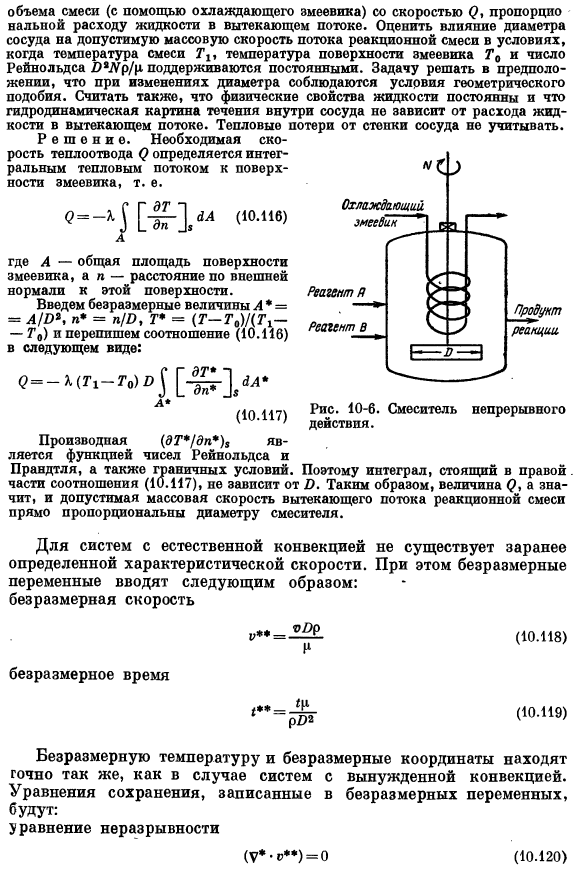
В уравнении сохранения (10.113)-(10.115) число Рейнольдса Re = Idpp /μ], fr = [72/ GDL, число Прандтля PR = [CPR /% 1 и число Бринкмана* br = (Gx— — Идти.]) Пример 10-7.Обмен шлама в контейнере с конвекцией Т агитатор. Две жидкости Поток непрерывно перемешивается 10-6.Нормальный. Путем непрерывного отвода тепла из емкости со смесителем схематично ОТС Условия эксплуатации> * Во многих текстах отношение (Br / Pr)= V * / Cₚ(Ti-To) рассматривается как одна безразмерная группа и называется числом Эккарта (Ec).ясно, что выбор независимых безразмерных групп произволен. Число Эккерта однозначно связано с числом Маха (см. выпуск 10-10).
Для систем с естественной конвекцией не существует предписанной характеристики speed. In в этом случае безразмерные переменные вводятся следующим образом: безразмерная скорость (10.118) Безразмерное время (10.119) Безразмерная температура и безразмерные координаты определяются точно так же, как и в системах с принудительной конвекцией.
- Уравнение хранения, описываемое безразмерной переменной, выглядит следующим образом: Непрерывные уравнения Уравнение движения Де * * Д | ** Gr- (10.121) Уравнение энергосбережения ДТ * 1 дл * * РГ Т » (10.122) Поэтому уравнение сохранения, описывающее систему с естественной конвекцией, содержит только 2 безразмерные группы: число Pr пландлов и число Gr = / gp2P (Г, -, Г₀)О3/И2].Заметим, что термин, описывающий вязкую диссипацию, опущен в уравнении сохранения энергии (10.122). Совер- Понятно, что процесс осуществляется в естественных условиях. Конвекция, вязкая диссипация не играют существенной роли. Где а-площадь спирали.
Индекс относится к слою жидкости и непосредственно примыкает к поверхности спирали. g-расстояние вдоль нормали этой поверхности. Перепишите выражение (10.123) для безразмерных переменных. ВОПРОС Д Д Ш 1 Х (разъем RJ-T₀) П (10.124) (10.125) (10.126) Один Об Этом Сообщил Источник The Sun. (10.127) (10.128) Как правило, можно решить уравнение (10.129) относительно Gr и получить явную формулу для искомой разности T1-Tn. Поскольку физические свойства жидкости гипотетически не зависят от температуры, число Прандтля каждой конкретной жидкости имеет постоянную величину value.
Поэтому температура газового слоя у поверхности твердого тела, обладающего нулевой скоростью, может быть либо выше, либо ниже температуры торможения потока. Людмила Фирмаль
Ввиду этого, если мы решим формулу (10.129) относительно (Г,-Г.), то получим: В главе 9 уже показано, как отображаются безразмерные группы, отображаемые в приведенном выше примере, когда дифференциальные уравнения, описывающие конкретную систему, сводятся к безразмерной форме. Проведенный выше анализ размеров был единственной целью показать, что одна и та же безразмерная группа может быть получена в рамках общих уравнений в частных производных, применимых как к изотермическим, так и к неизотермическим процессам. Размерный анализ используется в последующих главах, посвященных соотношению коэффициентов теплопередачи.
Может быть полезно рассматривать безразмерные группы как отношение между различными силами или эффектами, присутствующими в конкретной системе.* ППГ (7 ′ О-Г-и) (10.131) Молекулярная теплопроводность 。Молекулярный пепел」 Теплопроводность Итак, тот факт, что числа Рейнольдса малы、 Малое значение большего числа Бринкмана означает тепло, выделяющееся в системе в результате вязкости Молекулярный механизм теплопроводности позволяет удалять энергию из системы. Решающую роль в формировании гидродинамики играет, если соотношение Gr / Re2 велико Текущий паттерн воспроизводится путем поднятия силы.
Вопрос для обсуждения * Инерционный эффект уравнений движения выражается термином p (o-vol, форма вязкого члена представлена формулой zuo. To чтобы получить «типичную» оценку этих терминов, необходимо заменить переменные, которые их вводят, соответствующими характеристическими «масштабами» и ввести безразмерные переменные. Подробный Из этой системы? Пиар Решение ура геристи- Вам нужно получить формат D / di формата «D / D».
Смотрите также:
| Сводка уравнений сохранения | Уравнения сохранения для неизотермических систем. Задачи |
| Использование уравнений сохранения для решения задач о теплообмене | Нестационарный теплообмен в твердых телах |

