Как уже говорилось раньше, линией второго порядка называется линия, определяемая уравнением 2-й степени:
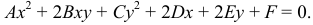
Запишем дискриминант уравнения 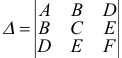 и дискриминант
и дискриминант
старших членов 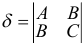 .
.
1) Если 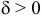 и
и 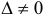 , то кривая 2-го порядка — эллипс (действительный или мнимый).
, то кривая 2-го порядка — эллипс (действительный или мнимый).
2) Если 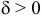 и
и 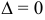 — точка.
— точка.
3) Если 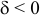 и
и 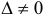 — гипербола.
— гипербола.
4) Если 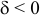 и
и 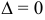 — пара пересекающихся прямых.
— пара пересекающихся прямых.
5) Если 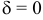 и
и 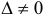 — парабола.
— парабола.
6) Если 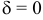 и
и 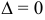 — пара параллельных прямых (действительных или мнимых).
— пара параллельных прямых (действительных или мнимых).
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Прямая линия в пространстве |
| Кривые второго порядка: эллипс, гипербола, парабола |
| Функция |
| Вычисление пределов функции |
