Оглавление:




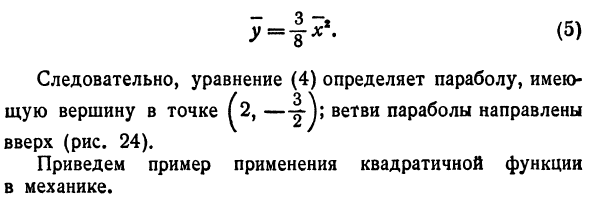
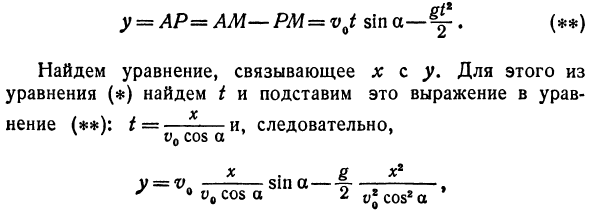




Исследование функции у = ах1 + Ьх + с
- Исследование функции y = ax1 + bx + c Функции, определяемые уравнениями y = ax + bx + c, (1) Это называется квадратичной функцией. Рассмотренная выше функция y = ax является частным случаем квадратичных функций. Наша цель — увидеть, как меняется уравнение (1) при переходе к новой координате. Получить новые оси Параллельно старой оси, т.е. ось Ox параллельна оси Ox%
Новые оси параллельны старым осям, а новый источник находится в точке (4, 1). B (4, -1), C (0, +1), D (3, -2). 2. Создайте параболу. а) Y = \ xr> б) Y = -y * 2- 3. Найдите тип и местоположение параболы y = x2-2x + 2 (сделайте так же, как в примере, показанном в тексте). 4. Найдите вершину y = -4 (x, +4 * +4) (используйте производную формулу). 5. Найдите тип и расположение параболы = -Зх1-24х — 50.
Если вам известны старые координаты, найдите координаты точек в новой системе: A (6, 2), Людмила Фирмаль
И ось Oy-ось Oy. Масштаб оси и направление совпадают со старым. Пусть координаты новой начальной точки старой системы равны x0 и y0. Замените формулу (5) вместо Формула через X и новые координаты: x-x + x0, Y ^ Y + Y — Получить == + P ^ — Решение этого уравнения для у ^ = ax * + (2ax0 + b) x + (ax1 + bx + c-y0). (2) Новые стартовые координаты в вашем распоряжении, так что вы можете выбрать для удовлетворения ваших требований 2ax0 + b = axl + bx0 + c-y0 = 0.
Эти уравнения имеют два неизвестных, x0 и yQ. Найди их: _ B_ 2a9 синица b * b2 т yo = ax0 + bx0 + c = a ^ -2- ^ + _ 4ac — b О U-4d _ / b 4ac — b \ Точка (- ^ — 1 занимает новое начало, В выражении (2) круглые скобки (2ax0 + b) и (для 😕 + — [- C- ^ yj равны нулю, что означает, что выражение (2) имеет следующий вид: у = ax2. (3)Полученное уравнение будет в форме, описанной выше.
- Таким образом, уравнение y = ax1 + bx + c для новой системы координат определяет ту же параболу, что и уравнение y = axl. Вывод: Уравнение y = ax% + bx + c определяет параболу, B_ 4 ac — b1 2 ay 4 a И филиалы Есть автобус Если a> 0, то он направлен вверх, если <0, то направлен вниз. Один и тот же вывод может быть выражен по-разному. График квадратичной функции Увеличивается, если задержка составляет> 0, уменьшается, если a <0. Эта ветвь Point bus
Пример 1. Нахождение типа и положения параболы, заданной уравнением y = jx * —Yx * Переместите начало координат в точку (x0, y0), координаты которой еще не известны. Старые координаты xy y представлены новыми x, y по формуле. х = х + х0, у = у + у0. Подстановка этих уравнений в уравнение (4) дает: s- «, / s 3 \ -, / 3 I 3 \ Y = mx + u xo-m) x + (mx ° —2x> Выберите новые начальные координаты, чтобы соблюдалось равенство. 4 около 2 ‘
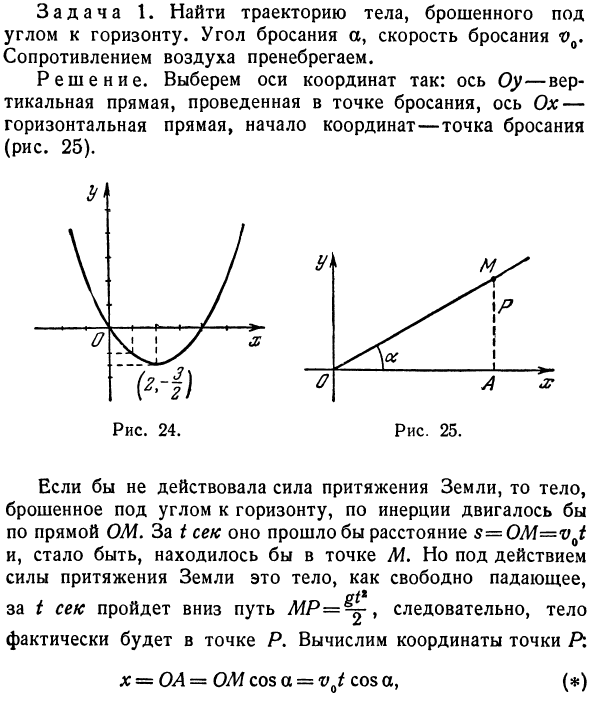
Таким образом, перемещение начала координат в точку ^ 2 превращает уравнение (4) в новое уравнение вида В результате уравнение (4) определяет параболу с вершиной в точке ^ 2. Параболическая ветвь Вверх (рисунок 24). Вот пример применения квадратичной функции в механике.
Решение полученной системы уравнений дает Lgo == 2> l-4-2, -T-2-4-8 — T- Людмила Фирмаль
Задача 1. Найти траекторию объекта, брошенного под углом к горизонту. Угол литья a, сопротивление воздуха на медленной скорости игнорируется. Решения. Оси координат выбираются следующим образом: Ось Oy — вертикальная линия, проведенная в точке приведения, ось Ox — горизонтальная линия, а начало координат — точка приведения (Рисунок 25). в Рисунок 24. Рисунок 25.
Если гравитация Земли не действует, объект, брошенный по диагонали относительно горизонта, будет двигаться по инерции вдоль прямой ОМ. За t секунд он должен был пройти расстояние s = OM = v0t, как и в точке M. Однако под действием силы тяжести Земли этот объект свободно падает, В * Поскольку путь MP = ^ -down в t секунд, объект фактически является точкой P. Рассчитаем координаты точки P. x = OA = OM cos a = v0t cos a,
y = AP = AM — PM = vQt sin a— ^. () Найдите уравнение, связывающее x и y. Для этого найдите t из выражения (*) и присвойте это выражение выражению Соотношение (): t = -и. Таким образом, 4 ‘v0 cos a •• х г х2 y-V -sina— ~ —— ^ 0 v0 cos a 2 v * C0S2 a *или () Получено уравнение траектории движения тела. Как видите, это рассматриваемая квадратичная функция. Следовательно, поскольку коэффициент x1 отрицателен, объект, который движется горизонтально в безвоздушном пространстве вдоль параболы с вершиной, расположенной выше, движется горизонтально. Какая самая высокая высота тела на земле?
Чтобы ответить на этот вопрос, вам нужно найти вершину параболы. Как и предполагалось, вершины параболы имеют координаты B 4 ac — b2 2 a> y ~~ 4 a В этой задаче a ——— ^ -, b-tga и c = 0, 2vl cos2 a Координаты вершины равны этому v \ sin2 a 2v * 0 cos2 a tg a v \ sin 2a 2g-2g ‘ tg2 a-2uj cos2 a Y-4g Здесь найдите диапазон тела, то есть абсциссу точки падения. Для этого получим следующее уравнение с уравнением () y.
Найдите два значения x: x1 = 0 и x2 = c = 2v \ sin a cos a = v \ sin 2a: первое показывает точку приведения, второе показывает желаемую абсциссу точки падения показывает вам. Все эти соображения относятся к безвоздушным пространствам. В воздухе высота и дальность значительно уменьшены. 0 xtga 2cos2 a
Смотрите также:
| Парабола | Тригонометрические функции. Радианная мера угла |
| Параллельный перенос осей координат | Показательная функция |

