Оглавление:

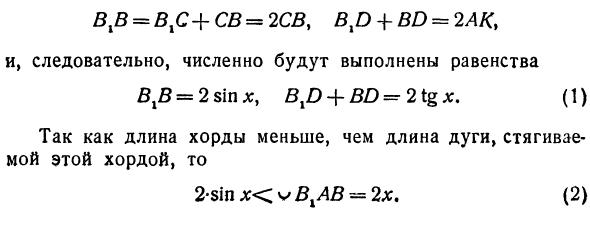

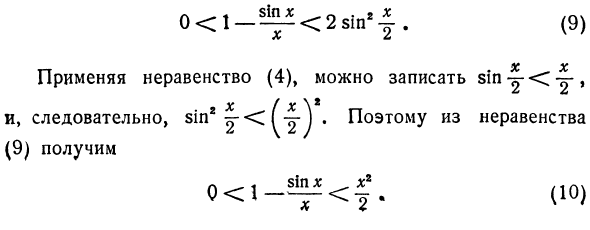


Исследование функции sin* при значениях
- Функциональное исследование Грех * По значению Независимая переменная с произвольно малым абсолютным значением Сначала запомните информацию из арифметики. а) Противоположное число — это число, деленное на это число. Например, числа Взаимное 3, 1/3, число, обратное Y2, число, обратное I, -. TS Рисунок 42. / 2 б) Если числа a и b удовлетворяют неравенству 0 y. c)
По мере уменьшения константы разница увеличивается, а вычитаемая разница уменьшается. Людмила Фирмаль
Давайте перейдем к исследованиям. Грех х Функция -. Давайте возьмем единицу радиуса круга и дугу AB над ней. Его радиус равен х (рис. 42). VCA касательная знак АК линия с АК Касательная к БД. В этом случае DSM / C = DS £> 5, /_OAK=Z.0BDr=z 90 ° »AA0B является обычным, а OA = OB˜ . BD = AK, потому что треугольники равны, то есть отрезок BD равен касательной. Поверните чертеж на 180 ° вокруг линии наружного диаметра.VHV = VgS + SV = 2 SV, BXD + BD = 2 AK> Поэтому равенство VHV = 2 см x, BXD + BD = 2 tgjc. (1) Поскольку длина шнура короче длины дуги, сжатой этим шнуром, 2-sin l: <v BHAB = 2x. (2)
Поскольку длина пунктирной линии, проведенной около дуги, больше, чем длина этой дуги, BYD + BD> v IHW или 2tg jc> 2x. (3) Из неравенства (2) О <грех л: <х. (4) Таким образом, положительный угол синуса всегда меньше, чем его аргумент. Из неравенства (3) t gx> x. (5) Объединение неравенств (4) и (5) 0 <грех х <х <тг х Или поделить на грех * 1 -> cos *. (7) х Вычтите из 1, cosjc и единиц. Я помню X ‘ Замечание в), мы 1 —1 <1—— <1 — cos *. (8) Преобразуйте это неравенство, введя синус полуширины.
- 0 <l_si ^ <2sinI |. (9) Х х Используя неравенство (4), sin y <Сy, Следовательно, s * nf («I») ‘Следовательно, из неравенства (9) 0 <1_! Ё £ <|. (10)Полученное неравенство (10) можно использовать для следующих выводов: Если х достаточно мало, он слишком мал. так Если независимая переменная х мала, 1 грех х „ Разница порядка I— заключена между нулем и малым х X2 Само значение y также мало. Этот вывод также может быть дан в следующем виде: Подойти к значению функции I-x X Принимает значения от нуля до нуля. И скажи так: функция I — ^^ х Если х стремится к нулю, это будет ноль. Слово «искать» обозначается символом.
Таким образом, предыдущий вывод можно записать в виде: -Грех х л л I — ► () x —► в условиях Людмила Фирмаль
(). X Обратите внимание, что ху равен греху х Ноль, дробь- * теряет смысл из-за деления на ноль Невозможно. Если функция I -► (), ^^ стремится объединиться, Поэтому все выводы, упомянутые в этом параграфе: Если независимая переменная стремится к нулю, функция имеет тенденцию быть одиночной. грех х, л —► Для меня, х— + 0. х
Смотрите также:
| Функция от функции, или сложная функция | Определения предела |
| Приращение функции | Свойства пределов |

