Исследование формы эллипса по его уравнению
Установим форму эллипса, пользуясь его каноническим уравнением.
1. Уравнение (11.7) содержит 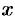 и
и 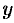 только в четных степенях, поэтому если точка
только в четных степенях, поэтому если точка 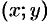 принадлежит эллипсу, то ему также принадлежат точки
принадлежит эллипсу, то ему также принадлежат точки 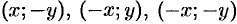 . Отсюда следует, что эллипс симметричен относительно осей
. Отсюда следует, что эллипс симметричен относительно осей 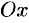 и
и 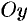 , а также относительно точки
, а также относительно точки 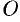 (0; 0), которую называют центром эллипса.
(0; 0), которую называют центром эллипса.
2.Найдем точки пересечения эллипса с осями координат. Положив 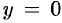 , находим две точки
, находим две точки 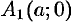 и
и 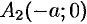 , в которых ось
, в которых ось
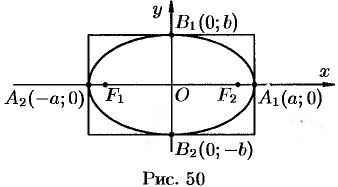
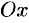 пересекает эллипс (см. рис. 50). Положив в уравнении (11.7)
пересекает эллипс (см. рис. 50). Положив в уравнении (11.7) 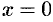 , находим точки пересечения эллипса с осью
, находим точки пересечения эллипса с осью 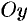 :
: 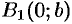 и
и 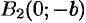 . Точки
. Точки 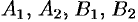 называются вершинами эллипса. Отрезки
называются вершинами эллипса. Отрезки 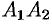 и
и 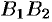 , а также их длины
, а также их длины 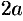 и
и 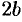 называются соответственно большой и малой осями эллипса. Числа
называются соответственно большой и малой осями эллипса. Числа 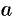 и
и 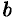 называются соответственно большой и малой полуосями эллипса.
называются соответственно большой и малой полуосями эллипса.
3. Из уравнения (11.7) следует, что каждое слагаемое в левой части не превосходит единицы, т. е. имеют место неравенства 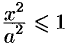 и
и 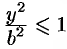 или
или 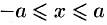 и
и 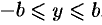 . Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми
. Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми 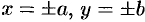 .
.
4. В уравнении (11.7) сумма неотрицательных слагаемых 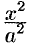 и
и 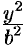 равна единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т. е. если
равна единице. Следовательно, при возрастании одного слагаемого другое будет уменьшаться, т. е. если 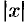 возрастает, то
возрастает, то 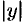 уменьшается и наоборот.
уменьшается и наоборот.
Из сказанного следует, что эллипс имеет форму, изображенную на рис. 50 (овальная замкнутая кривая).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Полярное уравнение прямой |
| Нормальное уравнение прямой |
| Дополнительные сведения об эллипсе |
| Уравнение равносторонней гиперболы, асимптотами которой служат оси координат |

