Оглавление:





Исследование автоколебаний на фазовой плоскости
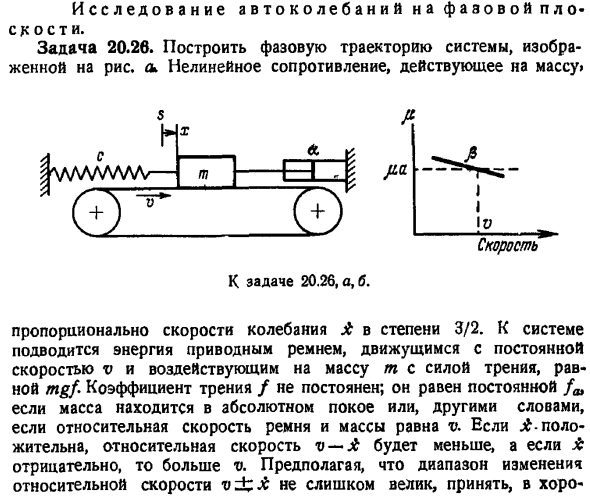
- Задача 20.26. Создайте фазовую траекторию для системы, показанной на рисунке. Нелинейное сопротивление, действующее на массу. Вопрос 20.26, а, б. Скорость колебаний пропорциональна отношению 3 2 к А. Энергия подается в систему приводным ремнем, который движется с постоянной скоростью y и действует на массу m с силой трения, равной коэффициенту трения. Если масса полностью неподвижна, то есть относительные скорости ленты и массы равны, а — положительны, то относительные скорости меньше, а если отрицательны, то больше V, то равны constant.
Короткое соответствие действительности, чтобы взять линейную зависимость коэффициента трения от D, то есть рисунок b а нет о Первоначально масса неподвижна в точке origin. At момент 0, внезапно добавился небольшой положительный импульс 0,0445 наносекунды. Решение. Опишите дифференциальное уравнение движения системы в виде Вы 4-в Х 1 2 х СХ м а 0А. 2 Если вы разделите обе стороны уравнения на m и переставите члены, вы получите а а 2-Пи х А х ой.
Для этого требуется выяснить, нет ли в твердом теле оси материальной симметрии либо плоскости материальной симметрии. Людмила Фирмаль
Эта формула ясно показывает, что линейная зависимость коэффициента трения от относительной скорости ленты и массы, принятая в задаче, приводит к появлению термина, и что динамический эффект этого термина равен эффекту отрицательного вязкого сопротивления. Если наклон П является отрицательной, демпфирующие срок п положительна, а система не автоколебание. Несколько сбоку мы предполагаем, что сопротивление системы не является мощностью 3 секунды, а пропорционально первой мощности скорости D. In в этом случае величина a-P определяет положительную или отрицательную вязкость friction.
Это указывает, является ли движение системы динамически устойчивым или неустойчивым, то есть любые небольшие возмущения исчезают, или система колеблется с непрерывно возрастающей амплитудой. Очевидно, что на практике a и P не остаются постоянными в достаточно широком диапазоне системных операций, поэтому разница между ними легко изменяется от плюса к минусу или наоборот. Учитывая это, при изучении автоколебаний следует сделать вывод о том, что нелинейные члены дифференциальных уравнений движения играют первостепенную роль и пренебрегать ими недопустимо.
Вернитесь к рассматриваемой системе и используйте Дельта-метод для решения уравнения 3.Переписан в стандартный-дель-Трум 4 Куда 6 и M P-M — pm — 5 Уравнение 4 ясно показывает, что существует среднее равновесное смещение, равное a11 системы рис. а. таким образом, поместите начало координат в начало координат x a kg в фазовой плоскости и создайте Дельта-кривую крика см. рис. с. Численное значение величины принимается следующим образом m 4.45 n, f0 0.5, s 175 n m, a 1b, 1 ssec — 2, Р 2,0 сек м.
В этих данных абсцисса среднего положения равновесия равна x — — 1,27 см. Собственная частота системы равна k 19,7 с-1, а формула для b 5 принимает вид 6 6 V 3 54t 3 2-0,98 в М. 6 При воздействии на Вену Масса, указанная в рассматриваемом условии, временно положительна L скорость равна 0,098 м с, а соответствующая координата приблизительно равна y 4 0,00497 м К — Фазовая точка A. вдали от этой точки мы строим фазовые траектории ранее рассмотренными графическими методами.
- Фазовые траектории расширяются спирально и достигают через 1 вращение точки B, 2 вращение точки C, 4 вращение точки E и небольшое вращение. После этого мы все ближе и ближе подходим к предельной траектории пунктирной линии. Разбитая дорожка показывает установившееся движение системы. Это соответствует Автоколебанию с амплитудой, равной примерно 7-кратному среднему равновесному смещению. Несмотря на то, что пересечение с координатными осями равноудалено от начала координат, эта орбита не является окружностью. Поэтому движение системы почти синусоидально. Этот фазовый след, представляющий собой установившееся автоколебание системы, называется предельным циклом.
Очень важно, чтобы траектория предельного цикла не зависела от начальных условий и последующих возмущений движения. Если начальное условие таково, что начальная точка фазы А находится вне предельного цикла, то точка фазы движется наружу по спирали, становясь все ближе к пунктирному пути. Показать me. At в первый момент к массе м прикладывают положительный импульс, который равен 1,35 нсек.
Если в твердом геле имеется ось материальной симметрии, то она является главной осью инерции твердого тела. Людмила Фирмаль
Тогда в момент времени 0 масса будет иметь положительную скорость R0 1.35 0.454 2.96 м с, а координата y0 Xa k будет V 2.96 19.7 0. 15 метров. Построить фазовые траектории этих начальных условий V О, 15, хо о. Начальная точка визуализации находится вне предельного цикла. Используйте любой шаг вдоль оси V для построения фазовой траектории. 1 первый шаг 0.1 V 0.15. 6 согласно среднему значению функции b на этом интервале является В 0.1 Д1 −1 Б г фин — 3.54 2-0.98 г л 0.035 м.
В 0.1 координата XG центр Ах Первая дуга фазовой траектории равна x1 −61 −0.035 м. от центра координаты −0.035 0 до начальной точки фазовой траектории координаты 0 0.15 начертите первую дугу с интервалом V 0.15 -. От 5 до 0,1. 2 2-й шаг 0,05 0,1. Среднее значение функции 6 на этом интервале аналогично первому шагу, 6a 0.0005.
Поскольку координата га ОГ-центр 2-й дуги га — 6а −0.0005 м, координата 2-й центр ОА −0.0005 0.От этого центра до конца первой дуги фазовой траектории нарисуйте 2-ю дугу с интервалом V 0.1 4-0. 05. 3 3-й шаг 0 0.05. Среднее значение функции 3-го интервала 6 равно 6E −0.0085 м. 3-я дуга создается таким же образом, как и предыдущая. Данные для следующего шага суммируются в таблице, которая предоставляется для проверки самостоятельной работы читателя. И так далее На рисунке d показана результирующая фазовая траектория конструкции. Эта извращенная беспомощность все больше приближается-тот же самый прогресс Цикл показан на рисунке. — бросил Джи.
Исходя из вышеизложенного, мы приходим к выводу, что поскольку предельный цикл представляет собой единственное стационарное движение системы, все точки фазы, которые не находятся на пунктирной траектории, включая промежуточную точку равновесия, представляют динамически неустойчивое состояние системы. В рассматриваемом примере орбита предельного цикла почти круговая, а стационарное движение Выпуск 20.26, г. Таким образом, это почти синусоидально, и частота самовозбуждения очень близка к k, собственной частоте системы без резистора.
Смотрите также:
Предмет теоретическая механика
| Автоколебания. Примеры автоколебательных систем | Геометрические величины, или векторы |
| Исследование автоколебаний аналитическими методами | Различные категории векторов |

