Задача 3.35.
Используя метод кусочно-линейной аппроксимации, найти максимальное значение функции
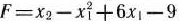
при условиях
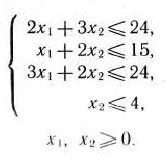
Решение:
В данном случае целевую функцию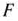 
можно представить как сумму двух функций
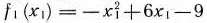
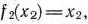
каждая из которых есть функция одной переменной. Следовательно, функция 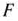является сепарабельной. Кроме того, она является погнутой (как сумма двух вогнутых функций), а область допустимых решений — выпуклой. Значит, используя метод кусочно-линейной аппроксимации, можно найти приближенно глобальный максимум целевой функции.
Здесь нелинейной функцией является только целевая функция. Значит, кусочно-линейной функцией следует заменить только ее. При этом так как функция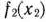 
линейная, то аппроксимировать будем функцию 
.
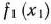На рис. 3.1, где построена область допустимых решений задачи, видно, что переменная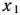 
может принимать значения в промежутке [0; 8]. Разобьем этот промежуток на восемь частей точками
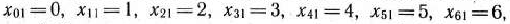
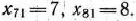
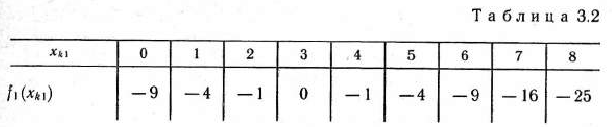
Вычислим теперь значения функции 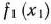в этих точках (табл. 3.2),
Используя формулы (86) и (87), находим
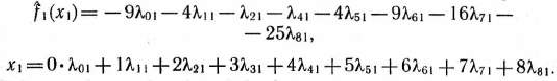
Подставляя найденные выражения 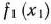и 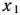в исходные данные, получим:
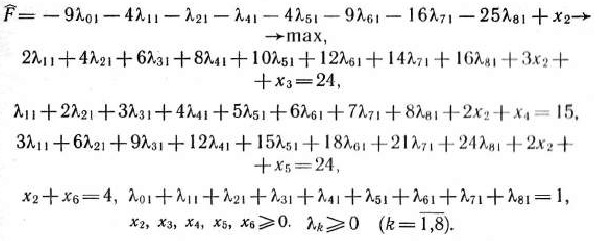
Для полученной задачи пять векторов
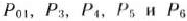
являются единичными. Значит, ее решение может Сын. найдено симплексным методом. Определяем его (табл. 3.3).
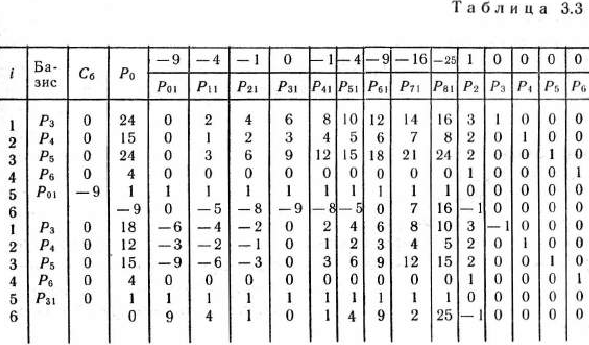
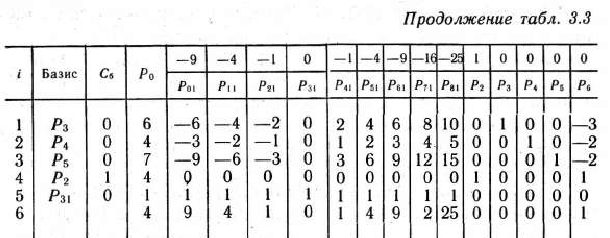
Далее, из табл. 3.3 видим, что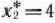 
. Значит, 
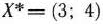является приближенным оптимальным решением, которое случайно совпало с точным решением. При данном решении 
.
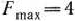Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
