Задача 2.10.
Используя метод аппроксимации Фогеля, найти опорный план транспортной задачи 2.1, исходные данные которой
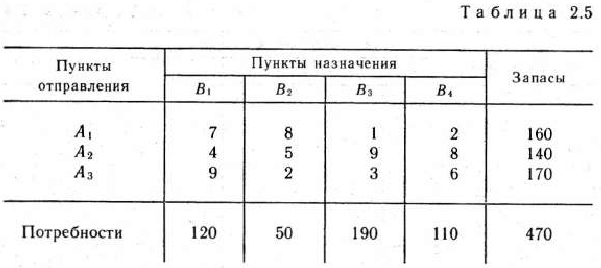
приведены в табл. 2.5 (опорный план этой задачи ранее был найден методом минимального элемента).
Решение:
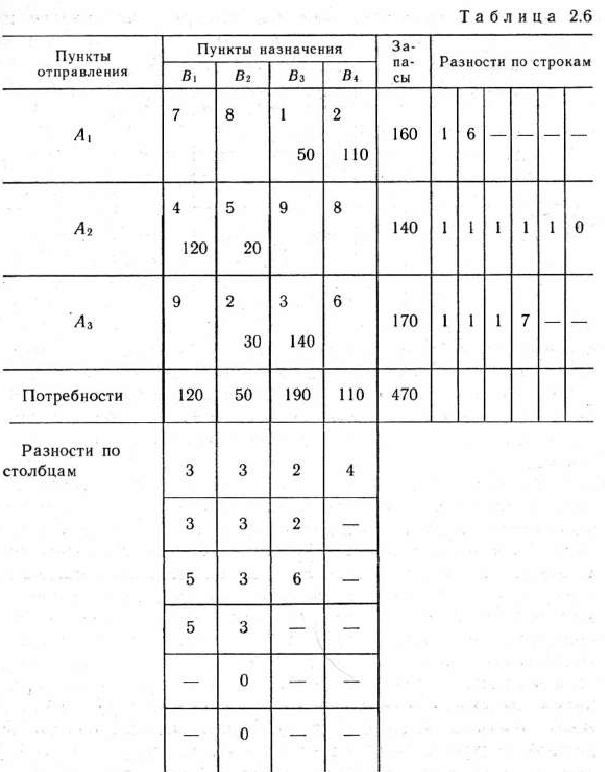
Для каждой строки и столбца таблицы условий найдем разности между двумя минимальными тарифами, записанными в данной строке или столбце, и поместим их в соответствующем дополнительном столбце или дополнительной строке табл. 2.6. Так, в строке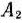 
минимальный тариф равен 4, а следующий за ним равен 5, разность между ними 5 — 4=1. Точно так же разность между минимальными элементами в столбце 
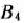равна 6 — 2=4. Вычислив все эти разности, видим, что наибольшая из них соответствует столбцу 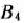. В этом столбце минимальный тариф записан в клетке, находящейся на пересечении строки 
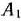и столбца 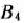. Таким образом, эту клетку следует заполнить. Заполнив ее, тем самым мы удовлетворим потребности пункта 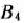. Поэтому исключим из рассмотрения столбец 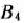и будем считать запасы пункта 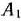равными 160—110 = 50 ед. После этого определим следующую клетку для заполнения. Снова найдем разности между оставшимися двумя минимальными тарифами в каждой из строк и столбцов и запишем их во втором дополнительном столбце и во второй дополнительной строке табл. 2.6. Как видно из этой таблицы, наибольшая указанная разность соответствует строке 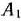. Минимальный тариф в этой строке записан в клетке, которая находится на пересечении ее с столбцом 
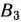. Следовательно, заполняем эту клетку. Поместив в нее число 50, тем самым предполагаем, что запасы в пункте 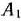полностью исчерпаны, а потребности в пункте 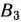стали равными 190—50 = 140 ед. Исключим из рассмотрения строку 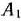и определим новую клетку для заполнения. Продолжая итерационный процесс, последовательно заполняем клетки, находящиеся на пересечении строки 
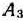и столбца 
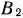, строки 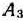и столбца 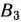, строки 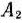и столбца 
.
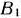строки 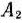и столбца 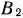. В результате получим опорный план
При этом плане общая стоимость перевозок такова:
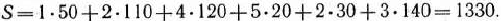
Как правило, применение метода апроксимаиии Фогеля позволяет получить либо опорный план, близкий к оптимальному, либо сам оптимальный план. Кстати, найденный выше опорный план транспортной задачи является и оптимальным.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
