Оглавление:







Использование уравнений макроскопических балансов для решения задач об установившихся течениях
- В разделе 3.5 для многих конкретных изотермических систем была упрощена система уравнений переноса импульса, на основе которой было получено дифференциальное уравнение, пригодное для расчета профилей скорости и давления. В этом разделе аналогичное упрощение сделано с уравнениями макроскопического баланса. Их цель-получить алгебру. Уравнение 7-1, описывающее гидродинамические свойства входа и выхода системы, показано на рисунке.
Представление будет далее ограничено стабильным изотермическим Снимите его с помощью электрического тока. ! Для каждой из следующих задач, че _ Явно макро уравнение 17 Общая форма берется и обсуждается скопикс баланс——; ——— g— Радель 7.1-7.3 ден — — — — — в— Оценочное значение отброшенного члена равно всем x ^ Предположения, лежащие в основе упрощения, тем самым определяя поток в трубе, внезапно определяют условия применимости end-conduitи серии результатов»^^: in ’в°вм-area».Например, «withdegree m%:°r — все приведенные примеры являются жидкими o предполагается, что incompressible. In осеннее сечение.
В приведенном уравнении р — плотность жидкости и Уо — скорость, которую имела бы жидкость, если бы не было ни одной частицы (скорость подхода). Людмила Фирмаль
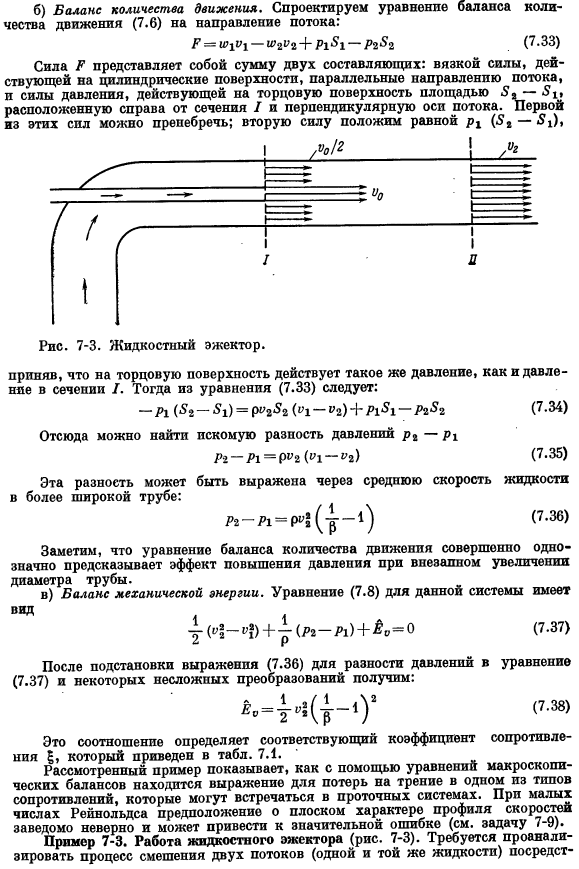
В задаче, связанной с потоком сжимаемых жидкостей и газов, необходимо учитывать теплоотдачу Обычно это очень значительный эффект. Эти задачи описаны в главе 14. Пример 7-2 повышенное давление и потери на трение из-за быстрого расширения труб. Турбулентность несжимаемой жидкости протекает по круглой трубе с площадью поперечного сечения 5.Эта труба соединена с широкой трубой сечением 8 г (рис.7-2).Использование уравнений / Г * | 7-3.Жидкостный эжектор. Такое же давление прикладывается и к поверхности лица. — П1 Нет. — 51)= ПВЗ долларов (КТ-«а)+ м> 151-группу pg3, перепада давления ПН — > 1 = ППН («1-» р) Сгоревший.
Формула «..это хорошая вещь.^Обратите внимание, что диаметр I-трубы значительно предсказывает эффект повышенного давления. в) баланс механической энергии. Уравнение (7.8) Предположим, что то же давление, что и давление в секции I, действует на торцевую поверхность. Тогда из Формулы(7.33) это выглядит так: — Р1 количество- «1)=» РМГ » («1-» ч)+ М1-Ra8g(7.34) Отсюда вы можете найти нужный перепад давления pg-p2. ПГ-Р1 = р» г («1—» г) (7.35) Эта разница может быть выражена средней скоростью движения жидкости по широкой трубе.
Количество импульса баланса, совершенно внезапное увеличение | (7.37) (7.37) и получить некоторые простые преобразования: 1 ′ 3⁸ Это соотношение определяет соответствующий коэффициент сопротивления 8. 7.1. «» Рассмотренный пример показывает, как формулу потерь на трение можно найти в 1 из видов сопротивления, которые могут возникнуть в проточной системе, используя формулу макроскопического баланса. Если число Рейнольдса мало, то предположение о плоских характеристиках профиля скорости явно неверно и может привести к серьезным ошибкам(см. выпуск 7-9). Пример 7-3 работа устройства для сброса жидкости (рис.
Вам нужно проанализировать процесс смешивания 2 потоков (одной и той же жидкости). После замены выражения (7.36) на разность q-некоторое простое преобразование, вы получаете: Уравнения баланса макросов. Поток сливается с плоскостью I, один из них движется со скоростью p at, занимает площадь поперечного сечения, равную «/ равной», а 2-й поток имеет скорость V на плоскости I, а площадь поперечного сечения с площадью » / s ^ g.
На достаточном расстоянии выбирается плоскость II (вниз по течению) от точки входа, поток в ней полностью перемешивается, а скорость жидкости практически постоянна, равна 2.Поскольку предполагается, что картина течения везде турбулентна, профиль скорости потока, сформированный после смешения с исходным потоком, на стенке Первого канала пренебрежимо мал. Государство: P1 ⁵1= p2 $ ₂ (7.39) p₂= p.
Из геометрии системы б) баланс числа движений, а проекция уравнения баланса выглядит так: В плоском виде профессиональное решение для среднего будет выглядеть так: 31.?2°) 3 P1 (7.42) (7.43) Замена этих пропорций а>,=и»,= ’/ЗрОф8, результат преобразования: После подстановки уравнения (7.41) и простого, применяем уравнение из условий материального баланса (7.44) Последняя формула определяет эффект увеличения давления смешивания 2 потоков. в) баланс механической энергии. Когда игнорировать членов Среднее соотношение составляет Вино H (NM -> 1 1T1, > ⁺г(т’,|>) _5.
- Подставляя эти выражения в уравнение (7.45) и используя соотношение (7.44), получаем: (7.48). Он начинается, и поток возникает в турбулентных потоках, которые повторились. Скромный Формула баланса массы является: Жидкостный эжектор. Однако в случае газовых эжекторов указанные результаты не являются applied. In в этом случае плотность \ 14-4 ° M состояние (°m-пример\пример 7-4.Сила, действующая на Жидкость конца колена, положение 1.1 атмосферы. Решение.
Число Рейнольдса потока в трубе диаметром 7,62 см » _ «(плотность Р = 0,962 г-см » •и в Вязе) 7-4.Реактивная сила, действие|> = 0,299 cP) равна: y⁰ — «» ход жидкости (интуитивно знают солнце-P P .4(57-10 «)-(0.962)。 _ A — ^ aa ^работает от порога-(7.62)•(0.00299) Здесь₽ — меньшее соотношение Больше. (7.50 )) По формуле (7.25) и данным, приведенным в таблице. 7.1, потеря трения ёо равна * / в данном примере、»-* /«= * /«Л-подставляя это значение в уравнение (7.50) и используя условие баланса массы (7.49), получаем: (7.51 )) Разность давлений на обоих концах колена с геометрическим коэффициентом р..
Зависимости для перепада давлений и переноса тепла в ожиженном слое определяются действительным состоянием, поэтому их весьма трудно описать. Людмила Фирмаль
Подставляя здесь формулу (7.51) для разности p₁-p, можно увидеть следующее: 5x =p45₂ (p-cos0)+(«^₂р −1 (а-1рз)+ +d5₂ (rch-soz6)= re’5; 1 +d5₂(П — 1-потому что Проекция уравнения баланса на сумму…. ..-это очень хорошо. Она записывается следующим образом (с учетом условий ω,= 0 и 5π,= 0): = «>2 ^ 2 — ₍ ₂ ₍ / −6??
Абсолютное значение силы P равно: (7.56) 1 * 1 = 1 (7-57) (7.58) Пятьдесят одни Уравнения равновесия механической энергии могут быть записаны в следующем виде, так как они не изменяются в процессе движения, которое не осуществляет работу на окружающую среду и возможности. 2а. г.
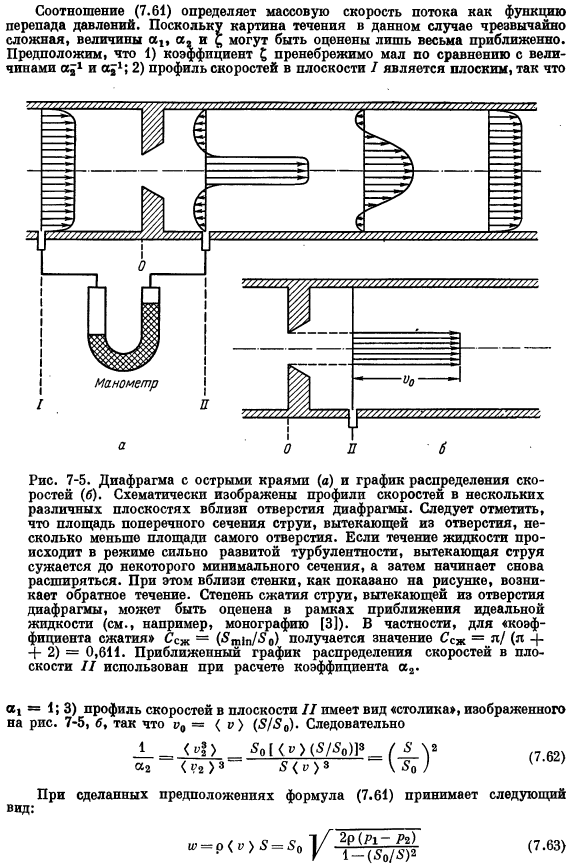
Где a и a-коэффициенты, в которых учитывается разница между величиной / .Принимая во внимание соотношение (7.59), мы можем получить выражение из выражения(7.60).И умножьте это на 5.、 (7.61) Посмотрев на расчеты, сделанные еще раз, вы легко увидите, что все эффекты, рассмотренные при решении задачи, важны. Исключение составляет сила, действующая на общую массу жидкости. Пример 7-5.Изотермический поток жидкости через диафрагму. Общий способ расчета массового расхода жидкости через трубу заключается в измерении перепада давления на «препятствии», помещенном в трубу. pipe.
Фактический измеритель диафрагмы используется, следующее уравнение выведено для скорости жидкости, проходящей через диафрагму: другие способы измерения затрат могут быть объяснены аналогичным образом. Мы рассмотрели положения испытательного клапана, соединенного с манометром. 7-5.Апертура с острыми краями (а) и график распределения скоростей (б).Схематическое изображение профиля скорости в нескольких различных плоскостях вблизи отверстия диафрагмы. Обратите внимание, что площадь поперечного сечения струи, протекающей через отверстие, немного меньше площади самого отверстия.
Если жидкость течет в сильно развитом турбулентном режиме, то проточная струя сужается до определенной минимальной площади поперечного сечения и затем начинает расширяться again. In в этом случае регургитация происходит вблизи стенки, как показано на схеме. Степень сжатия струи, протекающей через апертуру апертуры, можно оценить в рамках аппроксимации идеальной жидкости (например, см. монографию[3]).в частности, для «коэффициента сжатия» Csl =(⁵t1n /₀ 5) Величина Sez= / /(4 4- + 2)= 0.611 вы получите: примерный график распределения скоростей самолета sc был использован при расчете коэффициента sc. Перепад давления.
Фигура потока, когда задан диапазон, ранжирует a; 1 и a;1; 2) поскольку профиль скорости плоскости I является * плоским、 Эта формула определяет плотность жидкости в количестве ω, перепад давления (регистрируемый манометром) и зависимость от размеров трубы с помощью приведенного выше assumptions. In в инженерной практике в правую часть формулы (7.63) обычно вводится дополнительный коэффициент-так называемый коэффициент потока Sw’.
Смотрите также:

