Оглавление:
Использование свойств модулей
Упростить и решить некоторые из задач, содержащих модули, помогут знание и активное использование (там, где это оправданно) свойств модулей.
Отдельно можно выделить класс уравнений, в которых реализуется частный случай обращения какого-либо известного неравенства с модулями в равенство. При решении таких уравнений часто используется замена переменных, помогающая выявить, что данное уравнение есть случай обращения в равенство некоторого неравенства с модулями. Метод решения состоит в переходе к равносильному условию, принимающему форму неравенства или системы неравенств, но уже не содержащих модули (таким образом происходит избавление в задаче от модулей).
Приведём примеры равносильных преобразований, сводящих уравнение с модулем (модулями) к задаче, их не содержащей:
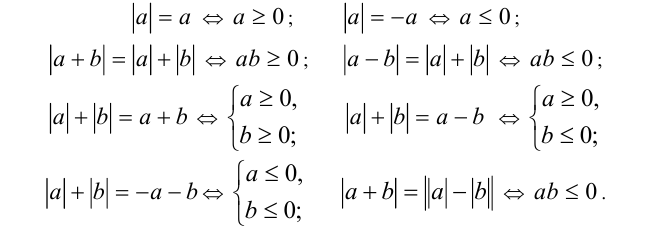
Обратимся теперь к рассмотрению задач указанного типа.
В первых трёх примерах используется свойство неотрицательности модуля: показан способ решения неравенств, в которых с одной стороны от знака неравенства находится нуль, а с другой — произведение (частное) нескольких сомножителей, один из которых имеет вид модуля некоторого выражения (следовательно, не меняет знака на ОДЗ). В этом случае рекомендуется рассмотреть два случая: когда этот сомножитель обращается в нуль, и когда он сохраняет положительный знак. В последнем случае на него можно поделить обе части неравенства, и задача упростится.
Пример №284.
Решить неравенство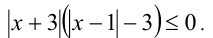 
.
Решение:
Заметим, что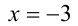 
— решение неравенства. Найдём другие решения. При 
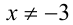сократим неравенство на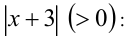 
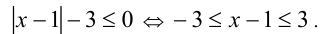Ответ: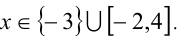 
Пример №285.
Решить неравенство
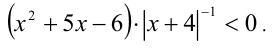
Решение:
Неравенство равносильно системе
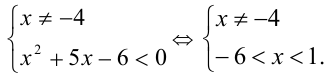
Ответ: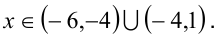 
Пример №286.
Решить неравенство
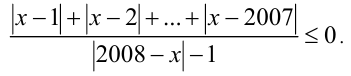
Решение:
Заметим, что числитель дроби положителен при любом действительном X (как сумма неотрицательных модулей, одновременно не обращающихся в нуль), поэтому в результате деления обех частей неравенства на этот числитель, приходим к равносильному неравенству
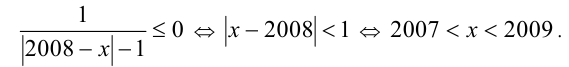
В следующем примере используются свойства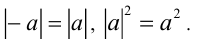 
Пример №287.
Решить неравенство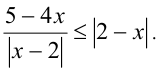 
Решение:
Так как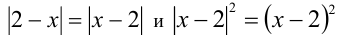 
Ответ: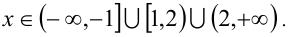 
В очередной задаче применение метода интервалов возможно лишь теоретически, зато использование простейшего свойства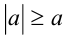 
(причём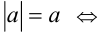 
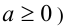позволяет эффективно решить уравнение.
Пример №288.
Решить уравнение
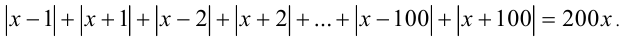
Решение:
Применим указанное свойство к каждому из двухсот модулей:
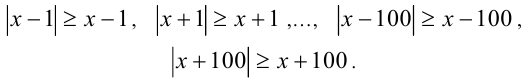
Складывая эти двести неравенств, получаем оценку:
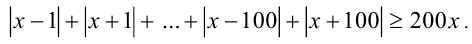
Осталось выяснить, когда последнее неравенство обращается в равенство. Это происходит тогда и только тогда, когда каждое из двухсот складываемых неравенств обращается в равенство. Таким образом, исходное уравнение равносильно системе
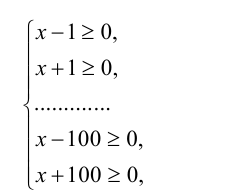
решая которую, находим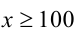 
. Ответ: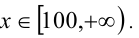 
В следующих примерах также демонстрируется применение различных свойств модулей.
Пример №289.
Решить неравенство
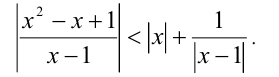
Решение:
Преобразуем неравенство:
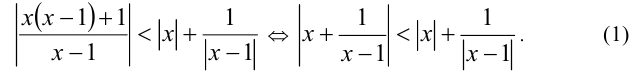
Воспользуемся для дальнейшего решения свойством модулей: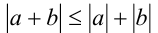 
при всех действительных 
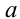и 
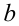. При этом неравенство обращается в равенство тогда и только тогда, когда числа 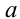и 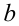имеют один знак или обращаются в нуль, т.е. когда 
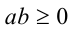. В остальных случаях (когда 
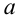и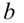 
разных знаков, т.е. 
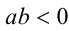) имеет место строгое неравенство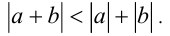 
Обозначая в рассматриваемом неравенстве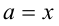
, 
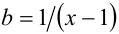получаем, что неравенство (1) равносильно более простому неравенству 
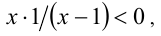решая которое, получаем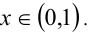 
Пример №290.
Решить неравенство
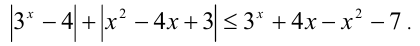
Решение:
Обозначим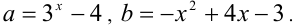 
Тогда имеем
Поскольку из свойств модулей известно, что при всех действительных 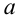, 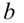справедливо 
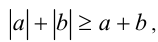то последнее неравенство совместно с (2) означает, что 
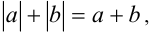что, в свою очередь, выполняется тогда и только тогда, когда одновременно 
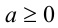и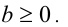 
Таким образом, исходное неравенство оказалось равносильно системе
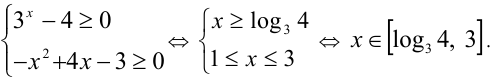
Пример №291.
Найти 
при условии
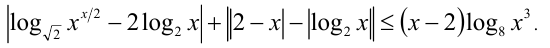
Решение:
Положим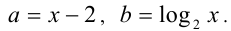 
Тогда исходное неравенство можно переписать в виде 
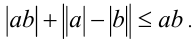С другой стороны, поскольку при любых действительных 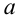, 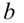справедливо 
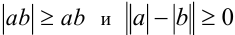, то, складывая последние неравенства, получим, что 
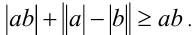Таким образом, имеем: 
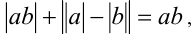что выполняется тогда и только тогда, когда
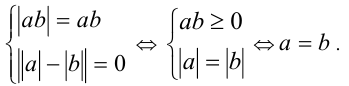
Итак,
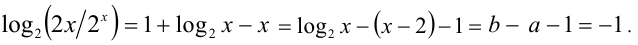
Пример №292.
Решить уравнение
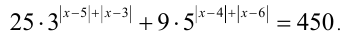
Решение:
Поделим обе части уравнения на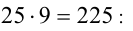 
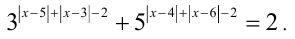
Так как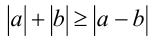 
(причём 
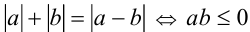), то имеем
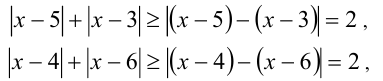
поэтому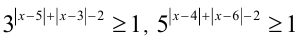 
и, следовательно,
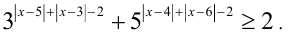
Равенство выполняется тогда и только тогда, когда
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
