Оглавление:
Использование различных алгебраических преобразований, в том числе формул сокращённого умножения, приёма выделения полных квадратов
Очень часто при решении задач используются различные алгебраические и прочие преобразования. Рассмотрим примеры такого рода.
Пример №59.
Доказать, что число
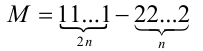
при любом натуральном п является полным квадратом.
Решение:
Так как число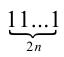 
представимо в виде 
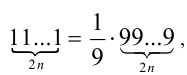, а число 
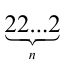, соответственно, в виде 
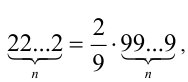то, подставляя в М и учитывая формулу 
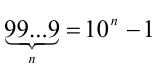,получим:
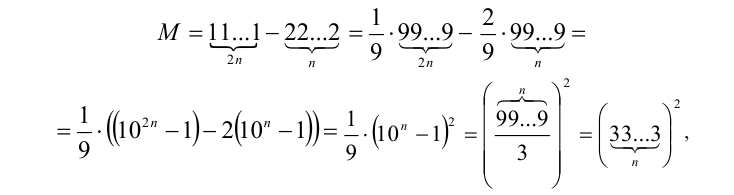
т.е. М при любом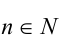 
является квадратом целого числа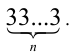 
Пример №60.
Найти сумму п первых членов ряда
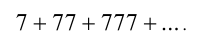
Решение:
Обозначим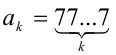 
— k -й член данного ряда. Требуется найти сумму
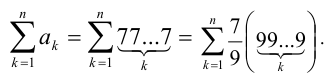Воспользовавшись формулами преобразований 
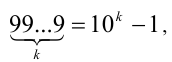а также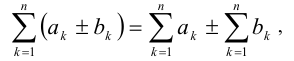 
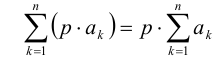получаем, что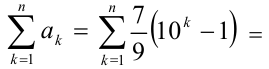 
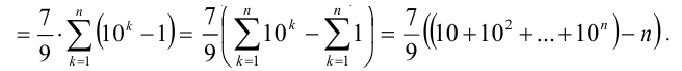
Применяя, далее, формулу для нахождения суммы первых п членов геометрической прогрессии, упрощаем выражение во внутренних скобках:
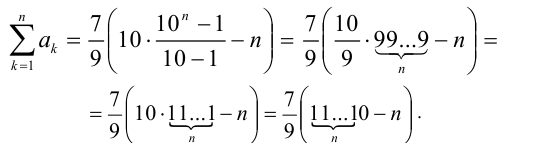
В очередных примерах решить задачу помогают формулы сокращенного умножения.
Пример №61.
Решить в целых числах уравнение
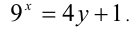
Решение:
1) При целом x < 0 в левой части равенства находится дробное число, а в правой — целое, что невозможно. Следовательно, в этом случае решений нет.
2) Перепишем уравнение в виде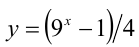 
. При целом 
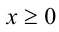выражение 
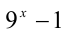можно разложить на множители:
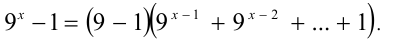
Отсюда следует, что это выражение делится нацело на 8, а значит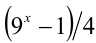
-целое число.
Ответ: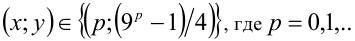 
Пример №62.
Найти две последние цифры числа
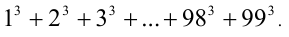
Решение:
Сгруппируем вместе первое слагаемое с последним, второе — с предпоследним и т.д.:
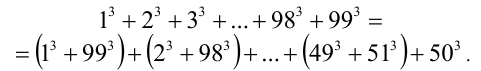
Воспользуемся формулой суммы кубов и преобразуем с её помощью каждое из выражений в скобках:
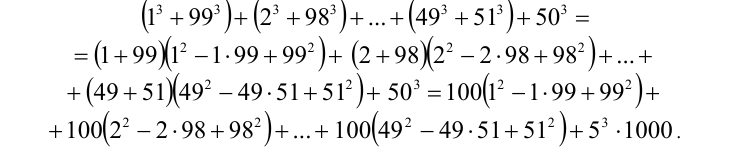
Очевидно, что каждое слагаемое, а значит, их сумма оканчиваются двумя нулями.
Пример №63.
Сумма десяти чисел равна нулю и сумма их различных попарных произведений равна нулю. Чему равна сумма кубов этих чисел?
Решение:
Обозначим эти числа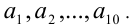 
По условию имеем:
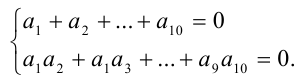
Подставляя эти данные в формулу сокращённого умножения
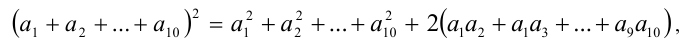
находим
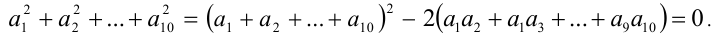
Это возможно, только если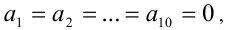 
но тогда
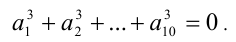
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
