Оглавление:
Иррациональные уравнения. Уравнения, содержащие знак модуля
1.Методы решения иррациональных уравнений, как правило, основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным уравнением, которое либо равносильно исходному иррациональному уравнению, либо является его следствием. Чаще всего обе части уравнения возводят в одну и ту же степень. При этом получается уравнение, являющееся следствием исходного.
При решении иррациональных уравнений необходимо учитывать следующее:
1) если показатель радикала — четное число, то подкоренное выражение должно быть неотрицательным; при этом значение радикала также является неотрицательным;
2) если показатель радикала — нечетное число, то подкоренное выражение может быть любым действительным числом; в этом случае знак радикала совпадает со знаком подкоренного выражения.
Рассмотрим уравнение вида
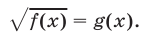
Если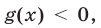 
то уравнение (1) не имеет корней, так как левая часть уравнения (1) не может принимать отрицательные значения ни при каких значениях 
.
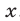Если же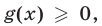 
то при возведении обеих частей уравнения (1) в квадрат получим равносильное уравнение. Таким образом, уравнение (1) равносильно системе
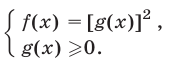
Замечание. При решении уравнения (1) нет необходимости предварительно находить ОДЗ левой части (1), решая неравенство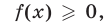 
которое может оказаться довольно сложным. Достаточно найти корни уравнения (2) и, не прибегая к непосредственной подстановке этих корней в уравнение (1), выяснить, какие из найденных корней удовлетворяют неравенству (3). Эти корни, и только они, являются корнями уравнения (1).
2.Из определения модуля (абсолютной величины) числа следует, что
1)
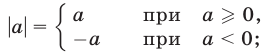
2) 
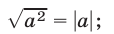
3) если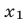 
и 
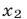— произвольные точки числовой оси, то расстояние между ними равно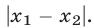 
Примеры с решениями
Пример №78.
Решить уравнение
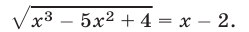
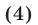
Решение:
Уравнение (4) равносильно системе
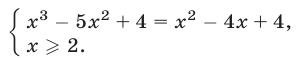
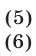
Уравнение (5), равносильное каждому из уравнений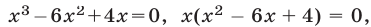 
имеет корни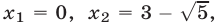 
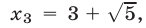из которых лишь корень 
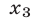удовлетворяет условию (6).
Ответ.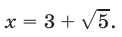 
Пример №79.
Решить уравнение
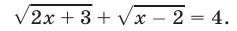
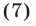
Решение:
Возведя обе части уравнения (7) в квадрат, получим уравнение
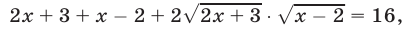
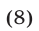
равносильное (7), так как обе части уравнения (7) неотрицательны. Уравнение (8) равносильно уравнению
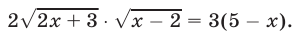
Возведя в квадрат обе части уравнения (9), получим уравнение
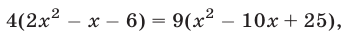
равносильное уравнению
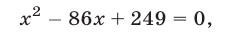
которое имеет корни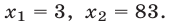 
Заметим, что уравнение (11) является следствием уравнения (7), так как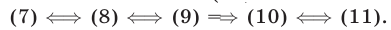 
Число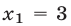 
— корень уравнения (7), а число 
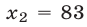— посторонний корень для уравнения (7): при 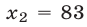левая часть уравнения (7) больше четырех.
Ответ.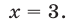 
В рассмотренном примере можно было сначала перенести один из радикалов в правую часть уравнения (метод уединения радикала), а затем возвести обе части полученного уравнения в квадрат.
Воспользуемся этим приемом при решении следующего примера.
Пример №80.
Решить уравнение
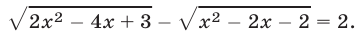
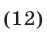
Решение:
Применив метод уединения радикала, получим уравнение
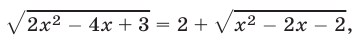
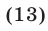
равносильное уравнению (12).
Заметим, что нет необходимости находить ОДЗ уравнения (13), но следует обратить внимание на подкоренные выражения. Если ввести новое неизвестное (выполнить замену переменной), полагая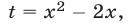 
, то уравнение (13) примет вид
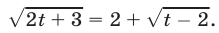
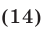
При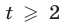 
(в ОДЗ уравнения (14)) это уравнение равносильно каждому из уравнений
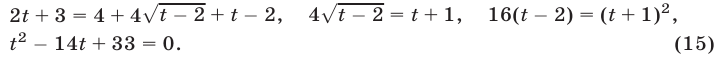
Корн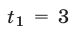и 
и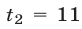 
уравнения (15) удовлетворяют условию 
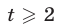и поэтому являются корнями уравнения (14).
Если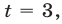 
то 
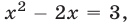откуда 
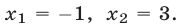Если 
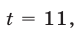то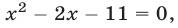 
откуда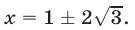 
Ответ.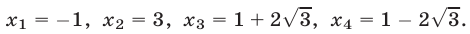 
В примерах 1-3 был использован метод возведения обеих частей уравнения в квадрат. В отдельных случаях применяются другие приемы, которые могут оказаться более эффективными.
Пример №81.
Решить уравнение
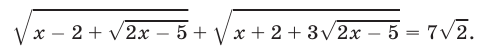
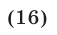
Решение:
Положим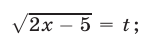 
тогда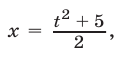 
и уравнение (16) примет вид
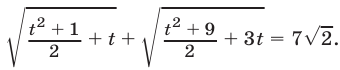
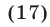
Уравнение (17) равносильно каждому из уравнений
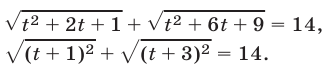
Используя тождество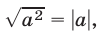 
запишем уравнение (18) в виде
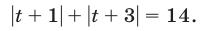
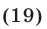
Так как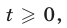 
то уравнение (18) и равносильное ему уравнение (19) можно записать в виде 
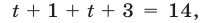откуда 
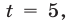т. е.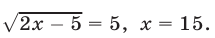
Ответ.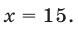 
Пример №82.
Решить уравнение
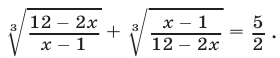
Решение:
Полагая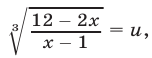 
преобразуем уравнение к виду
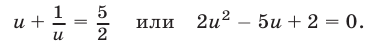
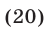
Уравнение (20) имеет корни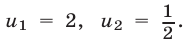 
Если 
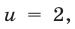то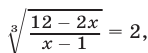 
откуда 
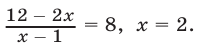Если 
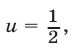то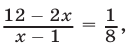 
откуда 
Оба найденных корня являются корнями исходного уравнения, так как в процессе решения было использовано (наряду с заменой неизвестного) только преобразование вида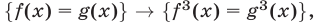 
при котором получается равносильное уравнение.
Ответ.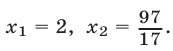 
Пример №83.
Решить уравнение
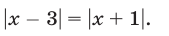
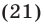
Решение:
Так как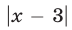 
и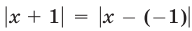 
— это расстояния от искомой точки 
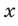до точек 
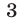и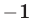 
соответственно, то из равенства (21) следует, что искомая точка 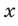находится на одинаковом расстоянии от точек 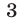и 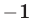. Таким образом, точка 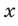— середина отрезка 
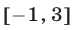и поэтому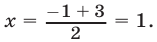 
Ответ.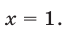 
Пример №84.
Решить уравнение
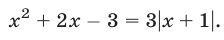
Решение:
Полагая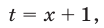 
получаем уравнение
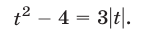
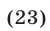
Если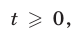 
то (23) имеет вид 
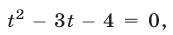откуда находим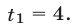 
Поскольку при замене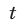 
на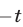 
уравнение (23) не меняется, число 
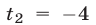также является корнем уравнения (23), а корни уравнения (2) — числа 
и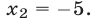 
Ответ.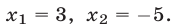 
Пример №85.
Решить уравнение
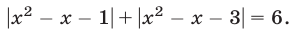
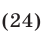
Решение:
Положим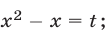 
тогда уравнение (24) примет вид
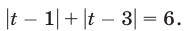
Решить уравнение (25) — значит найти все такие точки числовой оси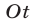 
(рис. 8.1), для которых сумма расстояний от каждой из них до точек 1 и 3 равна 6. Заметим, что искомые точки лежат вне отрезка [1,3], так как сумма расстояний от любой точки отрезка до его концов равна 2.
Пусть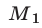 
— искомая точка, лежащая правее точки 3; 
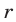-расстоя-ние от точки 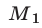до точки 3, 
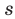— сумма расстояний от точки 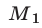до точек 3 и 1. Тогда 
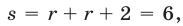откуда 
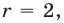а точке 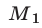соответствует число 
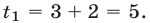Аналогично, корнем уравнения (25) является точка 
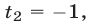находящаяся на расстоянии 2 от точки 1.
Таким образом, задача сводится к решению уравнений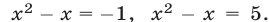 
Первое из них не имеет действительных корней, а второе имеет два корня.
Ответ.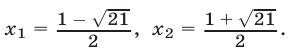 
Пример №86.
Решить уравнение
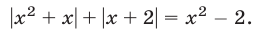
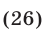
Решение:
Функция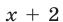 
меняет знак при 
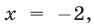а функция 
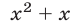— при 
и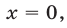 
причем 
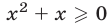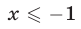при 
и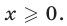 
Поэтому
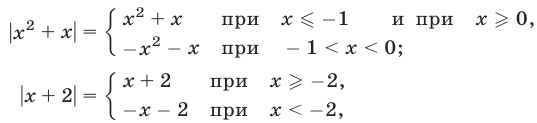
а уравнение (26), записанное без знака модуля на промежутках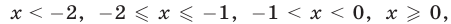 
равносильно совокупности следующих систем:
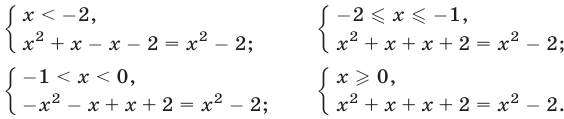
Первой из этих систем удовлетворяют все значения 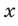из промежутка 
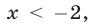второй системе — значение 
остальные две системы не имеют решений.
Ответ.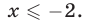 
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
| Уравнение и его корни. Преобразование уравнений |
| Рациональные уравнения примеры с решением |
| Показательные уравнения примеры с решением |
| Логарифмические уравнения примеры с решением |
