Для связи в whatsapp +905441085890

Иррациональные системы с двумя неизвестными с примерами решения

Иррациональные системы с двумя неизвестными

Если уравнение является иррациональным, то рассматриваются лишь действительные решения этого уравнения.

При этом предполагается, что в случае корня четной степени подкоренное выражение принимает неотрицательные значения и берется неотрицательное значение корня. В случае корня нечетной степени подкоренное выражение может принимать любые действительные значения и знак корня совпадает со знаком подкоренного выражения.

Пример №181.

Решить систему уравнений

Иррациональные системы с двумя неизвестными с примерами решения

Решение:

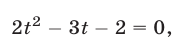
Первое уравнение подстановкой Иррациональные системы с двумя неизвестными с примерами решенияпреобразуется к виду

Иррациональные системы с двумя неизвестными с примерами решения

откуда Иррациональные системы с двумя неизвестными с примерами решения Так как Иррациональные системы с двумя неизвестными с примерами решения то второй корень отбрасываем.

Решив систему

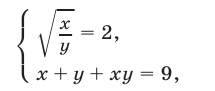
Иррациональные системы с двумя неизвестными с примерами решения

найдем два ее решения Иррациональные системы с двумя неизвестными с примерами решения и Иррациональные системы с двумя неизвестными с примерами решения которые являются решениями и исходной системы.

Ответ. Иррациональные системы с двумя неизвестными с примерами решения

Пример №182.

Решить систему уравнений

Иррациональные системы с двумя неизвестными с примерами решения Иррациональные системы с двумя неизвестными с примерами решения

Решение:

Умножив обе части (1) на выражение Иррациональные системы с двумя неизвестными с примерами решения сопряженное левой части этого уравнения, получаем

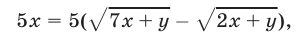
Иррациональные системы с двумя неизвестными с примерами решения

или

сИррациональные системы с двумя неизвестными с примерами решения Иррациональные системы с двумя неизвестными с примерами решения

Из (3) и (2) следует, что

Иррациональные системы с двумя неизвестными с примерами решения Иррациональные системы с двумя неизвестными с примерами решения

Складывая почленно уравнения (4) и (5), имеем

Иррациональные системы с двумя неизвестными с примерами решения Иррациональные системы с двумя неизвестными с примерами решения

Но тогда из (6) и (1) находим Иррациональные системы с двумя неизвестными с примерами решения откуда

Иррациональные системы с двумя неизвестными с примерами решения Иррациональные системы с двумя неизвестными с примерами решения

Каждое из уравнений (3)-(7) является следствием системы (1), (2). Исключив 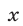Иррациональные системы с двумя неизвестными с примерами решения из системы (4), (7), получим

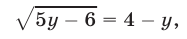
Иррациональные системы с двумя неизвестными с примерами решения

откуда Иррациональные системы с двумя неизвестными с примерами решения Иррациональные системы с двумя неизвестными с примерами решения

Соответствующие значения 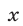Иррациональные системы с двумя неизвестными с примерами решениянаходим по формуле (7): Иррациональные системы с двумя неизвестными с примерами решенияИррациональные системы с двумя неизвестными с примерами решения Проверка показывает, что пара чисел Иррациональные системы с двумя неизвестными с примерами решения не является решением системы, а пара чисел Иррациональные системы с двумя неизвестными с примерами решения образует решение системы.

Ответ. Иррациональные системы с двумя неизвестными с примерами решения.

Замечание. Легко убедиться в том, что «лобовое» решение, основанное на избавлении от корней в исходной системе с помощью возведения в квадрат, связано с преодолением немалых трудностей.

Пример №183.

Решить систему уравнений

Иррациональные системы с двумя неизвестными с примерами решения Иррациональные системы с двумя неизвестными с примерами решения

Решение:

Запишем уравнение (9) в виде

Иррациональные системы с двумя неизвестными с примерами решения Иррациональные системы с двумя неизвестными с примерами решения

и возведем обе части уравнения (10) в квадрат. Получим Иррациональные системы с двумя неизвестными с примерами решения откуда

Иррациональные системы с двумя неизвестными с примерами решения Иррациональные системы с двумя неизвестными с примерами решения

Уравнение 11 является следствием системы (8), (9). Подставляя 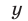Иррациональные системы с двумя неизвестными с примерами решения из (11) в уравнение (8), получаем

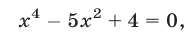
Иррациональные системы с двумя неизвестными с примерами решения

откуда Иррациональные системы с двумя неизвестными с примерами решения

Остается найти соответствующие значения Иррациональные системы с двумя неизвестными с примерами решения по формуле (11) и сделать проверку.

Ответ.Иррациональные системы с двумя неизвестными с примерами решения

Пример №184.

Решить систему уравнений

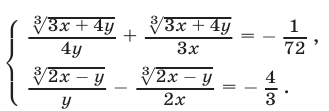
Иррациональные системы с двумя неизвестными с примерами решения

Решение:

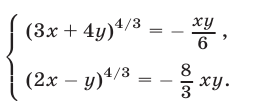
Заметив, что Иррациональные системы с двумя неизвестными с примерами решениязапишем систему в виде

Иррациональные системы с двумя неизвестными с примерами решения Иррациональные системы с двумя неизвестными с примерами решения

Разделив почленно уравнения системы (12), (13), получаем

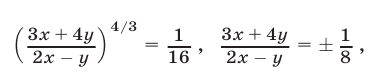
Иррациональные системы с двумя неизвестными с примерами решения

откуда

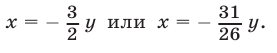
Иррациональные системы с двумя неизвестными с примерами решения

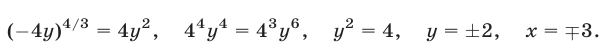
Если Иррациональные системы с двумя неизвестными с примерами решения то из уравнения (13) находим

Иррациональные системы с двумя неизвестными с примерами решения

Если Иррациональные системы с двумя неизвестными с примерами решенияИррациональные системы с двумя неизвестными с примерами решенияИррациональные системы с двумя неизвестными с примерами решения

Ответ. Иррациональные системы с двумя неизвестными с примерами решенияИррациональные системы с двумя неизвестными с примерами решенияИррациональные системы с двумя неизвестными с примерами решения

Пример №185.

Решить систему уравнений

Иррациональные системы с двумя неизвестными с примерами решения Иррациональные системы с двумя неизвестными с примерами решения

Решение:

Освобождаясь в уравнении (14) от иррациональности в знаменателях, получаем

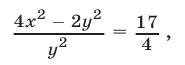
Иррациональные системы с двумя неизвестными с примерами решения

откуда Иррациональные системы с двумя неизвестными с примерами решения и Иррациональные системы с двумя неизвестными с примерами решения

В уравнении (15) положим Иррациональные системы с двумя неизвестными с примерами решения тогда получим Иррациональные системы с двумя неизвестными с примерами решения

откуда Иррациональные системы с двумя неизвестными с примерами решенияОтбросив корень Иррациональные системы с двумя неизвестными с примерами решения получим Иррациональные системы с двумя неизвестными с примерами решения

Решив две системы уравнений

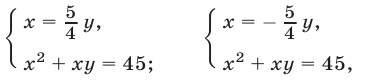
Иррациональные системы с двумя неизвестными с примерами решения

найдем четыре решения, которые, как показывает проверка, удовлетворяют и исходной системе.

Ответ. Иррациональные системы с двумя неизвестными с примерами решения

Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:

Решение задач по математике

Возможно вам будут полезны эти страницы:

Симметрические системы примеры с решением
Решение других типов систем алгебраических систем уравнений
Алгебраические системы с тремя неизвестными с примерами решения
Задачи на движение с примерами решения