Оглавление:
Иррациональными называют неравенства, в которых неизвестное или рациональная функция от неизвестного содержатся под знаками радикалов.
При решении иррационального неравенства следует сначала найти его ОДЗ, т. е. все значения неизвестного, при которых обе части неравенства определены (имеют смысл).
Иррациональное неравенство обычно сводят к рациональному, возводя обе его части в натуральную степень. Так как при этой операции может получиться неравенство, неравносильное исходному, то следует установить, при каких значениях неизвестного левая и правая части заданного неравенства принимают положительные или отрицательные значения.
Если обе части неравенства неотрицательны на некотором множестве, то при возведении их в натуральную степень получится неравенство, равносильное исходному на этом множестве.
Примеры с решениями
Пример №264.
Решить неравенство
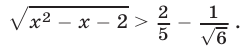
Решение:
Множество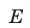 
допустимых значений (ОДЗ неравенства) определяется условием 
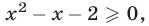откуда находим 
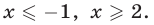При всех 
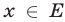левая часть неравенства неотрицательна, а правая часть — отрицательное число, так как 
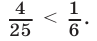Следовательно, все значения 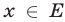и только эти значения являются решениями неравенства.
Ответ.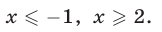 
Пример №265.
Решить неравенство
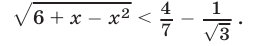
Решение:
Заметим, что 
поскольку 
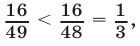а левая часть неравенства неотрицательна. Поэтому данное неравенство не имеет решений.
Ответ. Нет решений.
Пример №266.
Решить неравенство
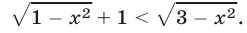
Решение:
Левая часть неравенства (1) определена при условии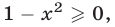 
т.е. на множестве 
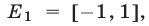а правая часть — на множестве 
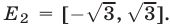Поэтому ОДЗ неравенства (1) — пересечение множеств 
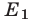и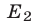 
, т.е. множество 
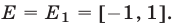На множестве 
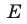обе части неравенства (1) определены и неотрицательны и поэтому оно равносильно неравенству
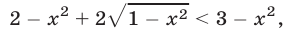
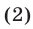
полученному возведением в квадрат обеих частей неравенства (1). Далее, неравенство (2) равносильно неравенству
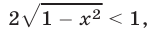
которое равносильно на множестве 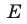каждому из неравенств
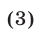
Таким образом, решениями неравенства (1) являются все те и только те числа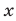 
из отрезка 
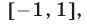которые удовлетворяют условию (3).
Ответ.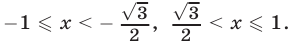 
Пример №267.
Решить неравенство
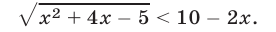
Решение:
Первый способ. Область допустимых значений неравенства (4) определяется условием
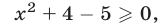
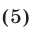
а множество 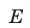решений неравенства (5) — объединение промежутков 
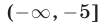и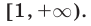 
Числа из множества 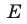, и только они, могут быть решениями неравенства (4).
Заметим, что левая часть неравенства (4) неотрицательна при всех 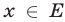, а правая часть меняет знак при переходе через точку 
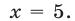Поэтому следует рассмотреть два возможных случая: 
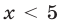и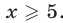 
1) Если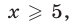 
то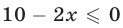 
и неравенство (4) не имеет решений, так как его левая часть неотрицательна.
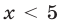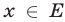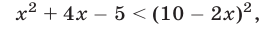
2) Если и , то обе части неравенства (4) определены и неотрицательны, поэтому оно равносильно неравенству
а неравенство (6) равносильно неравенству
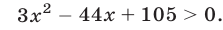
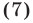
Чтобы решить неравенство (7), найдем корни уравнения
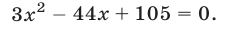
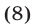
Получим
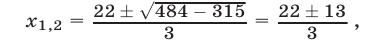
откуда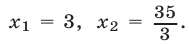 
Поэтому множество 
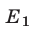решений неравенства (7) — объединение интервалов 
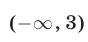и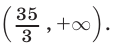 
Условиям 
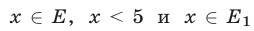удовлетворя-ют значения 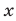из промежутков 
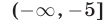и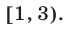 
Ответ.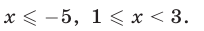 
Замечание. Рассуждения, приведенные при решении неравенства (4), дают основания утверждать, что неравенство
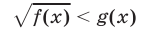
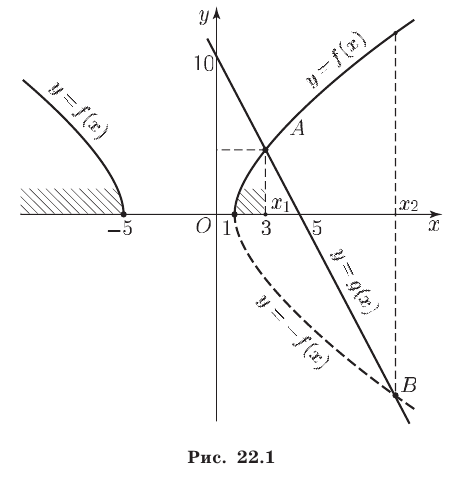
равносильно системе неравенств
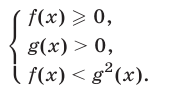
Второй способ. Построим графики функций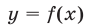 
и 
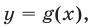где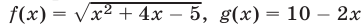 
(рис. 22.1).
Решить неравенство (4) — это значит найти все значения 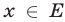, при которых график функции 
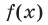лежит ниже графика функции 
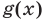. Абсциссы точек пересечения этих графиков — корни уравнения 
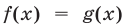. Это уравнение — следствие уравнения 
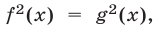т. е. уравнения 
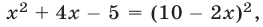которое равносильно уравнению (8). Из рис. 22.1 видно, что прямая 
пересекает график функции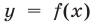 
только в точке 
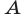, абсцисса 
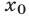которой— корень уравнения (8), принадлежащий отрезку 
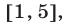т.е.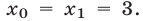 
Заметим, что корень 
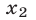уравнения (8) — это корень уравнения 
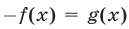(рис. 22.1), т.е. абсцисса точки 
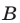, в которой прямая 
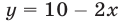пересекает график функции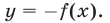 
Из рис. 22.1 заключаем, что график функции 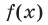лежит ниже графика функции 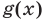на промежутках 
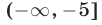и 
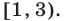
Пример №268.
Решить неравенство
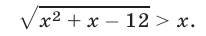
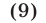
Решение:
Решив неравенство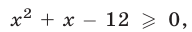 
, найдем ОДЗ неравенства (9), т.е. множество 
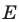(рис. 22.2), которое является объединением промежутков
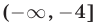и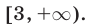 
Как и в примере 4, рассмотрим два случая: 
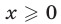и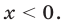 
1) Пусть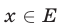 
и 
, т. е.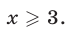 
Тогда обе части неравенства (9) неотрицательны. Возводя их в квадрат, получаем
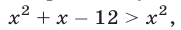откуда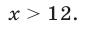 
Таким образом, все значения 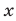из промежутка 
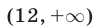принадлежат множеству решений неравенства (9).
2) Пусть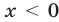 
, тогда правая часть неравенства (9) отрицательна, а его левая часть неотрицательна. Поэтому все значения 
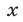такие, что 
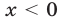и 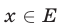(рис. 22.2), т.е. значения 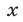из промежутка 
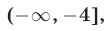являются решениями неравенства (9).
Ответ.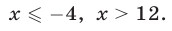 
Замечания. 1) Метод решения неравенства, использованный в примере 5, основан на том, что неравенство
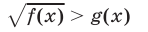
равносильно совокупности двух систем неравенств:
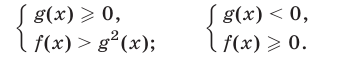
2) Многие абитуриенты, возводя в квадрат обе части неравенства (9) без учета знака его правой части, теряли множество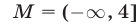 
решений этого неравенства.
Пример №269.
Решить неравенство
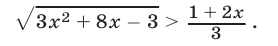
Решение:
Так как уравнение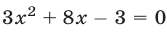 
имеет корни 
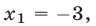то область 
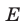допустимых значений неравенства — совокупность интервалов 
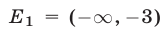и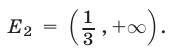 
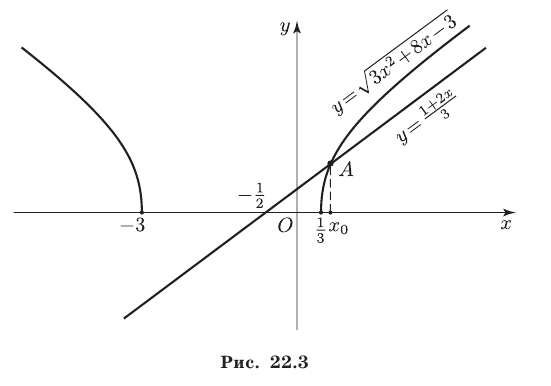
Решить данное неравенство — это значит найти все значения 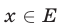при которых график функции 
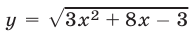лежит выше прямой
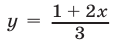(рис. 22.3).
Значения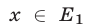 
являются решениями неравенства, так как 
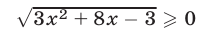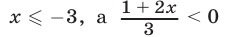при 
при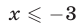 
(рис. 22.3).
Пусть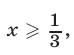 
тогда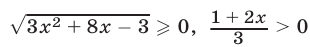 
и исходное неравенство равносильно каждому из неравенств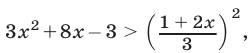 
Уравнение 
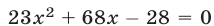имеет корни 
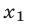и 
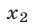, где 
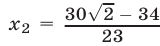(рис. 22.3). Поэтому решениями исходного неравенства на множестве 
являются все точки интервала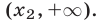 
Ответ.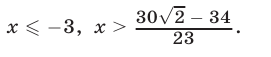
Пример №270.
Решить неравенство
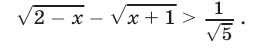
Решение:
Первый способ. Неравенство (10) равносильно неравенству
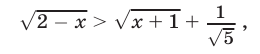
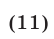
область определения которого — множество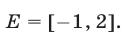 
Так как обе части неравенства (11) неотрицательны, то на множестве 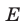оно равносильно неравенству
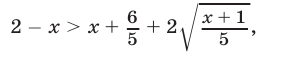
полученному возведением в квадрат обеих частей неравенства (11). Отсюда следует, что неравенство (11) равносильно системе неравенств
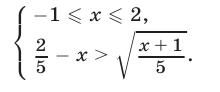
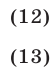
Если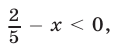 
т. е.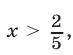 
то неравенство (13) не имеет решений.
Если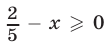 
и 
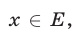т. е.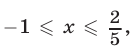 
то система (12), (13) 5 равносильна каждому из неравенств
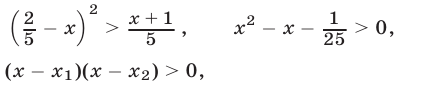
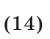
где числа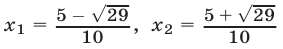 
являются корнями уравнения
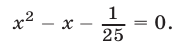
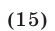
Решив неравенство (14) на множестве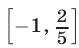 
и учитывая, что 
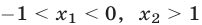(рис. 22.4), находим множество 
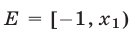решений неравенства (10).
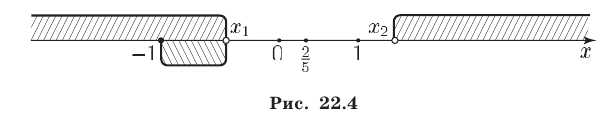
Ответ.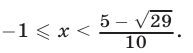 
Второй способ. Рассмотрим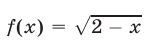 
и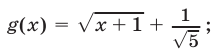 
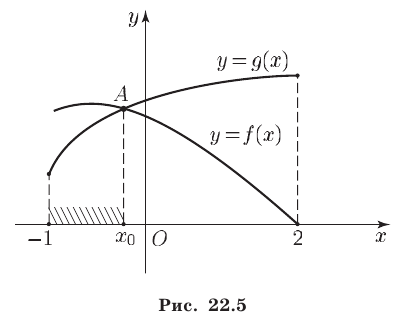
общая область определения этих функций — отрезок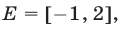 
а эскизы графиков представлены на рис. 22.5.
Решить неравенство (11) — это значит найти все значения 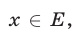при которых график функции 
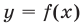лежит выше графика функции 
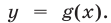Функция 
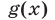является возрастающей, а функция 
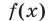— убывающей на множестве 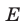, причем 
а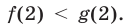 
Поэтому на отрезке 
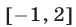графики этих функций имеют единственную общую точку 
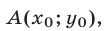где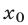 
(рис. 22.5) — корень уравнения 
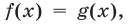т. е. уравнения (15). Заметим, что 
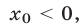так как 
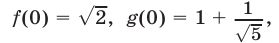Следовательно, 
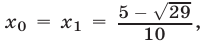а искомое множество решений неравенства (10) промежуток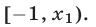 
Пример №271.
Решить неравенство
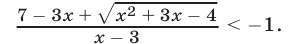
Решение:
Исходное неравенство равносильно неравенству
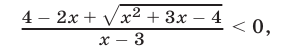
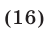
а неравенство (16) равносильно совокупности следующих двух систем неравенств:
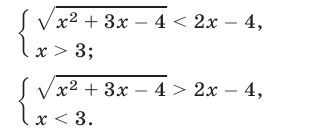
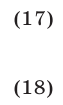
Множество допустимых значений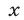 
для систем (17) и (18) определяется условием 
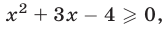откуда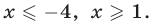 
а) При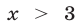 
обе части первого неравенства системы (17) положительны, а система (17) равносильна каждой из систем
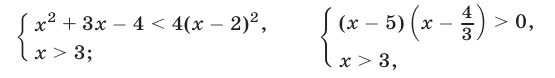
откуда следует, что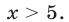
б) Системе (18) удовлетворяют значения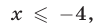 
так как при 
левая часть первого неравенства системы (18) определена и неотрицательна, а правая отрицательна; значения удовлетворяют и второму неравенству системы (18).
Значения 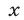из отрезка 
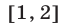удовлетворяют системе (18), а при 
система (18) равносильна каждой из систем
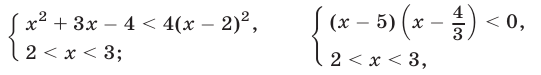
откуда следует, что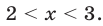 
Ответ.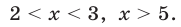 
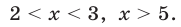
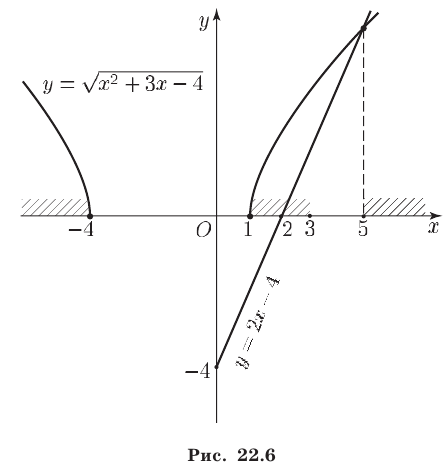
Замечание. Системы (17) и (18) можно решить, построив графики функци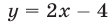й 
и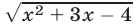 
(рис. 22.6).
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
