Оглавление:



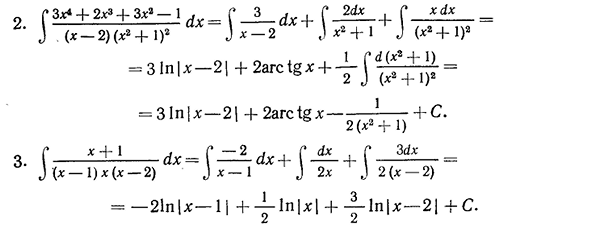

Интегрируемость рациональной дроби в элементарных функциях
- Интегрируемость рациональной дроби в основной функции. В настоящей работе предлагается общий метод решения задачи интегрирования рациональных дробей и вещественных коэффициентов. Прежде всего, эта задача может быть выражена как сумма алгебраического многочлена и нормальной рациональной дроби (путем деления числителя на знаменатель»столбец»). П ри м ЕР.
x* — X3 4-1×2+X+2 (x2-2x)+ 4x-R1x2 4×4-2′ Для Н4-Н3 4-1-ха+он+2х2-2х3-2х2 4-1-2х3-2х2-4х / x2 4-x4-2×2-2x Вы можете интегрировать оставшиеся 1 4-4X полиномы(напомним, что неопределенный интеграл полиномов является полиномом степени и выше этого). Осталось научиться правильно интегрировать рациональную дробь. Благодаря теореме 8.4
задача интегрирования положительной рациональной дроби сводится к интегрированию простейшей дроби из четырех типов -. В и_ _ _ в_ «jjjj L4x4-D’, ly L4x4-D x-b'(x-b/ ‘x2 — +RH4-g» Людмила Фирмаль
(x2 4-RH4 — (8.54) Здесь(3=2, 3,… ;З=2,3,… ;B, M, N, b, p, q-некоторые вещи — §3. Класс интегрируемой функции в базовой функции 319 Число, а тройка x2+px+q не имеет истинного корня, т. е. q — — — — — — >0. Четыре. Доказано, что каждая из этих четырех дробей интегрируется в основную функцию. Дроби формы I и II интегрируются в начальном порядке путем подстановки t=x-b. Для вычисления интеграла от дроби вида III приведем три квадратных члена, учитывающих n+px+q=++[I-I, q — — — p^2 ->. P0, мы пошлем фактическое- / R2 » R
Парковка=.+I / q-выполнив подстановку t — =x+ — имеем M и 2tdt(N_M P \ d t. 2J t2.+ a2+V.Два. M Cd (t+a)2J/2+a2I = — M, I n (,, r2+. а2г)—2-?- В — — — — А-ф-п АРК Т.г—т — — -, 1-с»= 2 2a икс —— В(нет. + px + q) H——2 N-M P A rc tg -.. _2+С.(8.57) — В’ — в’-4 Остается вычислить приведенный выше Интеграл. Из части IV типа.320CH. 8. Первичные и неопределенные интегралы M t+(n —— \ C_mX+N Д х = F___________2Д _ ДТ=J в(Х^+РХ+д^Дж(АС-А Р Ф=M_C д(ФЛ+<ФЛ) / г ‘м р\с di2J(З2+КЛЛ) к версии v2}Дж (ФЛ+А2)1’ Позвольте мне ввести обозначение Г С Д (ФЛ+<ФЛ)=Р ДТ Дж(ФЛ+Р Е Ф Альто Дж(ФЛ+Р Ф ) Если вычисляются интегралы I и KK, то
- вычисляется Интеграл интереса. Интеграл / базовая берется: Интеграл KX вычисляется нами в примере 6 в конце этой tlava§6. Там для этого интеграла мы получили итерационную формулу (3.12), которая позволяет непрерывно вычислять KK для любого L=2,3… Основываясь на этом факте — Дуга тг — +С. один Итак, мы вычислили интегралы всех четырех элементарных дробей(8.54) и доказали, что каждый из этих интегралов является основной функцией. Таким образом, мы приходим к следующим теоремам, исчерпывающим проблему интегрирования рациональных дробей. Т Е О Р Е А8. 5. Все
рациональные дроби с действительными коэффициентами интегрируются в основную функцию. В заключении этого раздела мы остановимся на примере вычисления неопределенного интеграла из рациональной дроби. Мы вычисляем неопределенный интеграл из трех дробей, описанных в предыдущих пунктах, (8.49), (8.50) и (8.53) -. Используя эти три формулы, формула (8.55) — аналогична (8.57), мы имеем: 1. 2 x 3+4×2 — [- x2(x-1)2 (x2 4-x-R1) дуплексный= дуплексный =2 1Р / ч-1 Три. (x-1) 2 Два. КЗ Дуга тг 2 x+1/3 +С. Что случилось?
Точнее, она выражается в терминах логарифмов, обратных касательных и Людмила Фирмаль
рационального Функа — §3. Класс интегрируемых функций в базовой функции 321 J, (x-2) (x2+1)2J x-2J X2+1J (x2+1)2 =31n / x-2 / +2arctx+^ — P(^I?Джей — ==3 1П|х-2|+2а радиоуправляемый тг х-2 (; С21—+С. 3. f___ *^+ ——d x=f^ — d x+f -= *Под термином «рациональная функция от одной переменной i» понимается рациональная дробь с вещественным коэффициентом от аргумента T. J(x-1) x (x-2)J X-1J2x J2(x-2) = — 21Р / ч—1| +- ^ — 1P|x / + — / — ln / x-2 / +C.
Смотрите также:
Методическое пособие по математическому анализу

