Оглавление:
Интегрирование выражений, рационально зависящих от тригонометрических функций
1. Рассмотрим интегралы вида 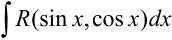 . Подстановка
. Подстановка
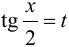 называется универсальной. Она сводит данный интеграл к интегралу рациональной дроби нового аргумента
называется универсальной. Она сводит данный интеграл к интегралу рациональной дроби нового аргумента 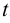 . При такой подстановке
. При такой подстановке
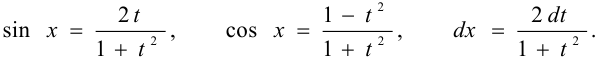
Задача №84.
Вычислить 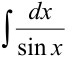 .
.
Решение:
Применим универсальную подстановку 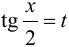 . Тогда
. Тогда 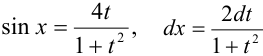 .
.
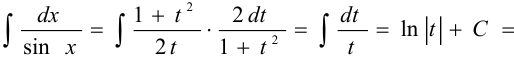
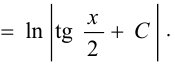
Иногда универсальная подстановка 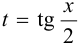 приводит к сложным выкладкам. Поэтому можно воспользоваться другими подстановками:
приводит к сложным выкладкам. Поэтому можно воспользоваться другими подстановками:
1) если функция 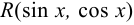 нечётная относительно синуса, то применима подстановка
нечётная относительно синуса, то применима подстановка 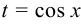 ;
;
2) если функция 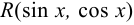 нечётная относительно косинуса, то применима подстановка
нечётная относительно косинуса, то применима подстановка 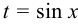 ;
;
3) если функция 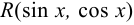 чётная относительно синуса и косинуса, то применима подстановка
чётная относительно синуса и косинуса, то применима подстановка 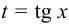 .
.
Задача №85.
Вычислить 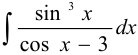 .
.
Решение:
Подынтегральное выражение нечётно относительно синуса, поэтому воспользуемся подстановкой 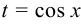 ,
, 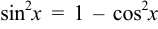 ,
, 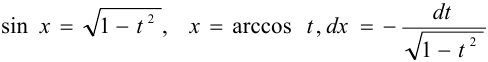 .
.
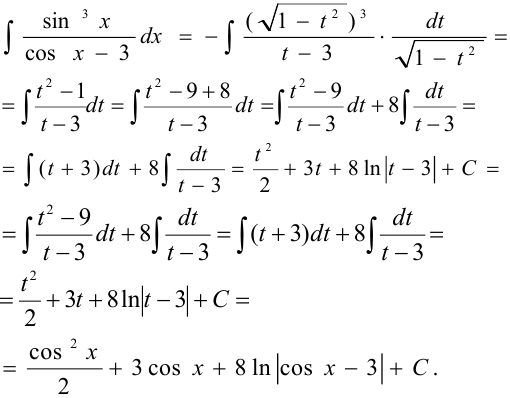
2. Рассмотрим интегралы вида:
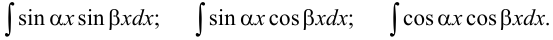
Для того, чтобы вычислить интегралы данного вида, воспользуемся формулами:
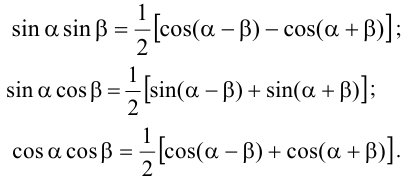
При этом каждое произведение превращается в сумму, интеграл от которой легко вычислить.
Задача №86.
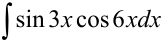 .
.
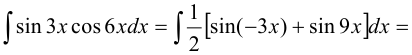
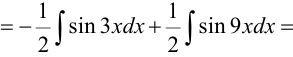
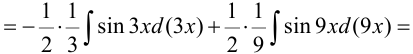
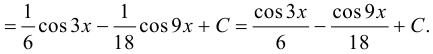
3. Рассмотрим интегралы вида: 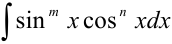 .
.
Следует различать два случая: а) хотя бы один из показателей 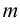 и
и 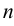 нечетный; б) оба показателя четные.
нечетный; б) оба показателя четные.
Пусть  , тогда:
, тогда:
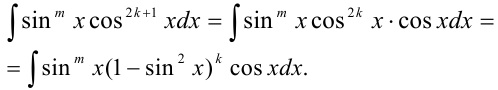
С помощью замены 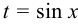 решение сводится к интегрированию
решение сводится к интегрированию
многочлена относительно 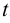 .
.
Если 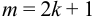 , то поступаем аналогично.
, то поступаем аналогично.
Если оба показателя 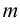 и
и 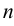 — четные числа, то используют формулы
— четные числа, то используют формулы
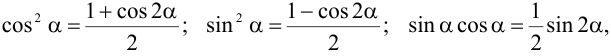
которые понижают показатели степени синуса и косинуса, после чего получится интеграл того же типа что и выше.
Задача №87.
Найти 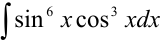 .
.
Решение:
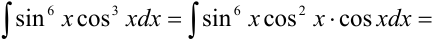
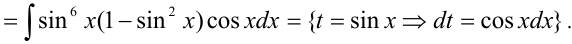
Имеем
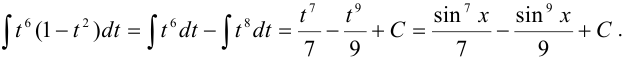
Задача №88.
Вычислить 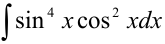 .
.
Преобразуем подынтегральную функцию:
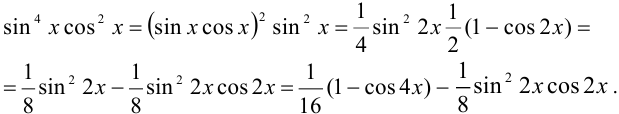
Тогда получим:
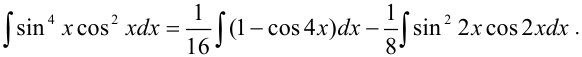
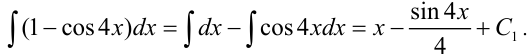
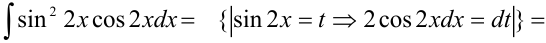
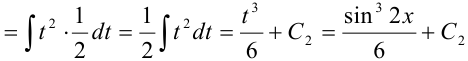 . Отсюда
. Отсюда 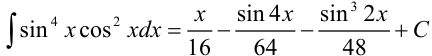 .
.
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:

