Оглавление:

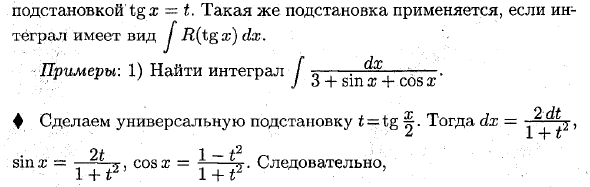

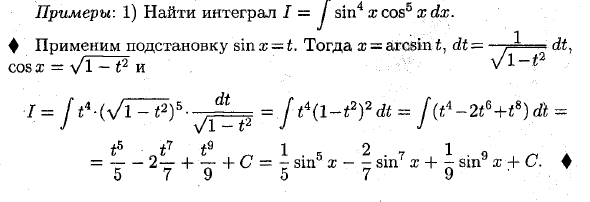
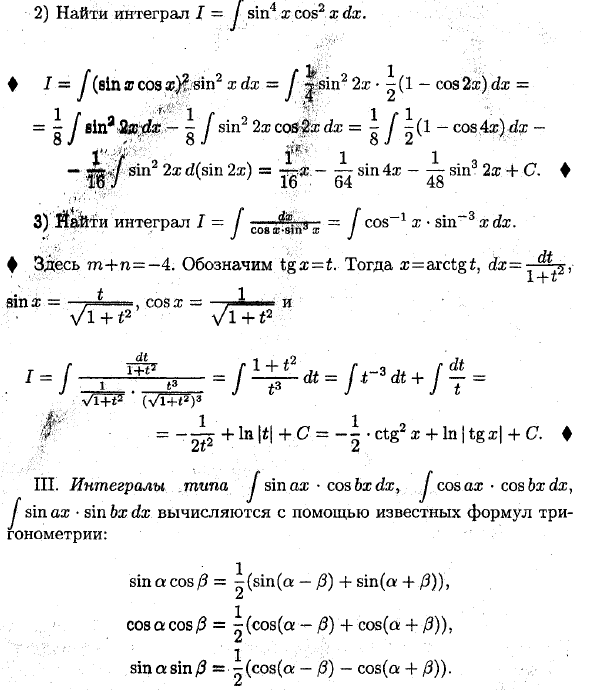
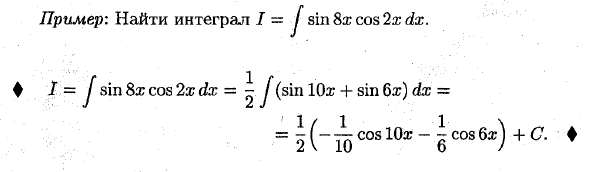
Интегрирование тригонометрических функций
- Триангуляционная интеграция функция Рассмотрим некоторые случаи, когда вы найдете тригонометрические интегралы. Функции с переменными sin и cosx, над которыми выполняются рациональные действия (сложение, вычитание, умножение, деление), обычно обозначаются ^ (sinx; coso;). R — знак рациональной функции. I. «Интеграции типа J te (sin a ;; cos g) dx. Они сводятся к интегралам рациональных функций заменой tg ^ =, называемой универсальной. GT L. -2TGF 21 1-TG2 F Конечно, грех a: == JT? ‘cosa: = 1 + tg2x = I -12 2 —- x-2 области. дх —- дт. так 1-М2 1 + Т2 J L (sin x \ cos x) dx = f ^ (j ^ ‘y’ J ^ fi dt «j Rl (t) dt>
Где R \ (/,) — рациональная функция от t. . На практике также используются другие более простые замены, в зависимости от свойства (и типа) подынтегрального выражения. В частности, полезны следующие правила: 1) Если функция # (sina ;; cos)) нечетна по отношению к греху, то есть R (-sin a:; cos-) = -H (sinx; cos)), то назначение cos a: = t рационализации; 2) Если функция R (sin a ;; cos x) нечетна относительно cos x, то есть R (sinx; -cos x) = -H (sina ;; cosx), sin x = t \ 3) Если функция H (sin x; cos x) четна по отношению к sin x и cos x R (-sin x; -cos x) = R (sinx; cos a :), интегрирование рационализируется
Этот метод обычно очень громоздок, но всегда приводит к результатам Людмила Фирмаль
Tg i = t путем подстановки. Такая же замена применяется, когда формой интегрирования является J R (tgx) dx. Пример: 1) Найти интеграл J ^ ^ ^ x грех х + соз х _ 2 дт Сделайте универсальную замену t = tg, тогда dx = K £ 1 — {- 1 о 1 1 _ J.2 Sin a; = i> cosx = ^ —так 1 т 1 Н-т 2 dt _ r dt ‘ x + cosx » J (i4; .t2) (3 + I | LT + i = ^) до} + 2 B (* + i) 2 VA * + i „2 1 -b 2 tg | Найти интеграл / = J y K v- g • 2 dt_ _ g_dt_ ~ J + ^ + ~ Jt * + t + sin2 x ‘iv # (-sinx; -cos g) = -m — m-yy = -a = J $ (sinx; cosx), • 1 + (-sin x) 2 1 4-sin x Затем введите tg x = t. Отсюда дт. О tg2® r = arctan t, = и так dt g dt Ir, д (у / 2т) d_ dt__ r dt _ 1 r ~ J (я 4- + Жл ~ J 2t2 + 1 ~ 7 МДж (1 + * 2) (1 + J 2t> + 1 ^ J (> / 2О2 + 1 » = я арктан \ / 2 £ + C = арктан (\ / 2 тг х) + C. ♦ I. Тип / интеграл от sinm a; • cosnxdx.
Для их поиска используются следующие методы: h 1) Если sin является нечетным положительным целым числом, подстановка sinx = t. 2) если замена cosx = m является нечетным положительным целым числом; 3) Формула сокращения: cos2 x = i (l + cos2x), sin2 w = 1-й / л = -cos2x), sinx • cosx = ^ sin2x, если тип является неотрицательным целым числом, даже. , 4) Если m + n — четное отрицательное целое число, заменить tgx = t
| Таблица основных интегралов | Интегрирование иррациональных функций |
| Основные методы интегрирования | «Берущиеся» и «Неберущиеся» интегралы |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Пример: 1) Найти интеграл / = J sin4 x cos5 x dx. ♦ применить замену sin x = t. Тогда x = arcsin dt =. ^ dt, cosx = n / 1-t’2 и vl- £ 2 1 = J t4 (l-t2) 2dt = f (t4-2te + t *) dl = t ** ‘t ^ t ^ 1st 2.7 1, Q. = -2 — t- + C = ~ sin5 x — sin7 x + -мы x + C. ♦ о (УоIУ2)
Найти интеграл I = J sin4 x cos2 x dx. ♦ I = / (sin®cos s}? Sin2 xdx = f |; Sin2 2x ♦ — (1-cos2я) dx = 1 / ■ ^ 1 r 1 rl «- = -J g J sin2 SovFxdx = -J- (1-cos4x) dx- — грех 2x d (грех 2g) = — грех 4x — грех 2x + C. ♦ t: fl 2оочfl 1 1 … 3 3) Найти интеграл I = J x = J cos 1 x • sin 3 xdx. ♦ где m + n = –4. tan £ = t Далее z = arctan £, dx = dt. мне 11 sin a: =, * «■ cosx => n и Vl + i2 дт ; vT + F (Vl-H *) 3 IF | = — ^ + ln | i | -fC7 = ~ i.ctg2x + ln | tgx | + C7. ♦ III. Интеграция типа J sin-топор cosbxdx, J cos топор cos bxdx} J sin ax • sin bx dx рассчитывается по известной тригонометрической формуле. sin a cos f3 = i (sin (a-ft) -f sin (a + ft)), z cos a cos = ^ (cos (a-0) + cos (a -f 0)), и грех грех = ■ i (cos (a- / 3) -cos (a + / 3)). Z
Пример: Найти интеграл / = / sin 8а; cos 2ж I = J sin 8х cos 2x dx = ~ J (sin lOrr 4- sin 6x) dx = 2 В 1 ( ч Л COS Юге — 7 cos 6a;) + C. 10 о / Людмила Фирмаль

